【最小生成树模型】
最小生成树(Minimum Spanning Tree)模型原理与应用
引言
最小生成树(Minimum Spanning Tree,简称MST)是图论中的经典问题之一,它在实际应用中有着广泛的应用。本文将介绍最小生成树模型的原理和应用,并通过一个实战项目来演示如何使用Python实现最小生成树算法。
最小生成树模型原理
最小生成树是一个连通无向图的生成树,它包含了图中所有的顶点,但只有足够的边来使得树连通且权重之和最小。最小生成树模型有以下两个基本性质:
- 最小生成树是一个树,即无环连通图。
- 最小生成树的权重之和最小。
最常用的求解最小生成树的算法是Prim算法和Kruskal算法。
Prim算法
Prim算法从一个起始顶点开始,逐步扩展最小生成树,直到包含所有顶点。算法的基本步骤如下:
- 选择一个起始顶点作为树的根节点,将其加入最小生成树。
- 从与最小生成树相邻的顶点中选择一个最短边连接到树上,将该顶点加入最小生成树。
- 重复步骤2,直到所有的顶点都被包含在最小生成树中。
Kruskal算法
Kruskal算法通过不断添加权重最小的边来构建最小生成树,直到所有顶点都被包含在树中。算法的基本步骤如下:
- 将图中的边按照权重从小到大进行排序。
- 依次从排序后的边中选择权重最小的边,若该边的两个顶点不在同一连通分量中,则将该边加入最小生成树,并将两个顶点合并到同一连通分量中。
- 重复步骤2,直到所有的顶点都被包含在最小生成树中。
最小生成树模型应用
最小生成树模型在实际应用中有着广泛的应用,以下是一些常见的应用场景:
网络设计
在计算机网络设计中,最小生成树模型可以用来构建网络拓扑结构,以便实现最优的网络连接。
物流和运输
在物流和运输领域,最小生成树模型可以用来确定最优的运输路线,以减少成本和提高效率。
电力传输
在电力传输网络中,最小生成树模型可以帮
助确定最优的输电线路,以减少能源损失和提高能源利用率。
集群分析
在数据分析和机器学习中,最小生成树模型可以用来进行集群分析,帮助发现数据集中的特定模式和关联性。
实战项目:最小生成树的应用
下面我们将通过一个例子来演示如何使用Python实现最小生成树算法。假设我们有一个城市的地图,我们需要找到连接所有城市的最优道路网络。
步骤
步骤1:准备数据
首先,我们需要准备城市地图的数据。数据可以包括城市之间的距离或权重,以及城市的坐标信息。在这个示例中,我们将使用一个包含5个城市的简单地图。
步骤2:构建图结构
使用Python中的图结构表示城市地图,并添加城市之间的边和权重。
import networkx as nx
# 创建图对象
G = nx.Graph()
# 添加城市之间的边和权重
G.add_edge('A', 'B', weight=4)
G.add_edge('A', 'C', weight=2)
G.add_edge('B', 'C', weight=1)
G.add_edge('B', 'D', weight=5)
G.add_edge('C', 'D', weight=8)
G.add_edge('C', 'E', weight=10)
G.add_edge('D', 'E', weight=2)
G.add_edge('D', 'F', weight=6)
G.add_edge('E', 'F', weight=2)
步骤3:求解最小生成树
使用Prim算法或Kruskal算法求解最小生成树,并获取最小生成树的边列表。
from networkx.algorithms import minimum_spanning_tree
# 使用Prim算法求解最小生成树
mst = minimum_spanning_tree(G, algorithm='prim')
# 获取最小生成树的边列表
edges = list(mst.edges(data=True))
步骤4:可视化结果
使用matplotlib和networkx库将最小生成树可视化。
# 创建画布和子图对象
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
# 绘制城市地图
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=500, node_color='lightblue', font_size=12, font_weight='bold', ax=ax)
# 绘制最小生成树的边
nx.draw_networkx_edges(G, pos, edgelist=edges, width=2, edge_color='red', ax=ax)
# 添加每条边的权重和初始节点
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=10)
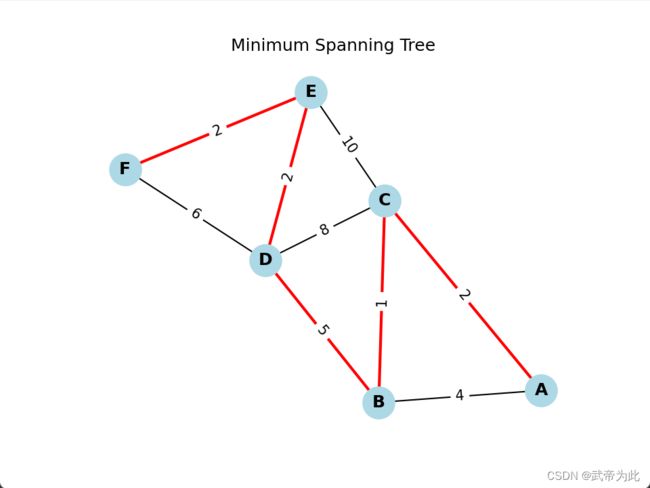
plt.title('Minimum Spanning Tree')
plt.axis('off')
plt.show()
结论
最小生成树模型在实际应用中有着广泛的应用。通过掌握最小生成树模型,我们可以在各种领域中找到最优的连接方式,以减少成本和提高效率。