python机器学习第七章：集成学习——组合不同模型

·基于多数投票的预测
·通过对训练数据集的重复抽样和随机组合降低模型的过拟合（bagging）
·通过弱学习机在误分类数据上的学习构建性能更好的模型

集成学习

集成⽅法（ensemble method）的⽬标是：将不同的分类器组合成为⼀个元分类器，与包含于其中的单个分类器相⽐，元分类器具有更好的泛化性能。
理论验证：预测精度高于百分之五十时，集成方法可以显著提升预测准确度

多数投票（majority voting）

均等多数投票

加权多数投票

import numpy as np
a = np.array([[2, 4, 6, 1], [1, 5, 2, 9]])
print(np.argmax(a))
print(np.argmax(a, axis=0)) #竖着比较，返回行号
print(np.argmax(a, axis=1)) #横着比较，返回列号

输出：
7
[0 1 0 1]
[2 3]

使⽤NumPy中的numPy.average和np.argmax⽅法：

在第3章中，我们学习了如何通过逻辑斯谛回归模型来计算样本相对于各类别的归属概率；在决策树中，此概率是通过训练时为每个节点创建的频度向量（frequency vector）来计算的。此向量收集对应节点中通过类标分布计算得到各类标频率值。进⽽对频率进⾏归⼀化处理，使得它们的和为1。类似地，k-近邻算法中，也会收集各样本最相邻的k个邻居的类标，并返回归⼀化的类标频率。
不同于决策树，逻辑斯谛回归与k-近邻算法（使⽤欧⼏⾥得距离作为距离度量标准）对数据缩放不敏感。虽然鸢尾花特征都以相同的尺度（厘⽶）度量，不过对特征做标准化处理是⼀个好习惯。

集成分类的成员分类器调优

调⽤⼀下get_param⽅法，以便对如何访问GridSearch对象内的单个参数有个基本的认识：

mv_clf.get_params()

得到get_params⽅法的返回值后，我们现在知道怎样去访问成员分类器的属性了。出于演⽰的⽬的，先通过⽹格搜索来调整逻辑斯谛回归分类器的正则化系数C以及决策树的深度。代码如下：

from sklearn.model_selection import GridSearchCV
params = {'decisiontreeclassifier__max_depth': [1, 2],
          'pipeline-1__clf__C': [0.001, 0.1, 100.0]}
grid = GridSearchCV(estimator=mv_clf,
                    param_grid=params,
                    cv=10,
                    scoring='roc_auc')
grid.fit(X_train, y_train)

bagging——通过bootstrap（又放回随机抽样）样本构建集成分类器

此算法没有使⽤相同的训练集拟合集成分类器中的单个成员分类器。由于原始训练集使⽤了boostrap抽样（有放回的随机抽样），这也就是bagging被称为boostrap aggregating的原因。
在实战中，分类任务会更加复杂，数据集维度会更⾼，使⽤单棵决策树很容易产⽣过拟合，这时bagging算法就可显⽰出其优势了。最后，我们需注意bagging算法是降低模型⽅差的⼀种有效⽅法。然⽽，bagging在降低模偏差⽅⾯的作⽤不⼤，这也是我们选择未剪枝决策树等低偏差分类器作为集成算法成员分类器的原因。

boosting算法——Adaboost(Adaptive boosting)

boosting主要针对难以区分的训练样本，也就是说，弱学习机通过在错误分类样本上的学习来提⾼集成分类的性能。
更新权重时提高错误分类权重，降低正确分类权重。
现在我们对AdaBoost的基本概念有了更好的认识，下⾯通过伪代码更深⼊地学习该算法。为了便于阐述，我们⽤⼗字符号（×）来表⽰向量的元素相乘，⽤点号（·）表⽰两个向量的内积，算法步骤如下：
虽然AdaBoost算法看上去很简单，我们接下来⽤下⾯表格中的10个样本作为训练集，通过⼀个具体的例⼦来更深⼊地了解此算法：

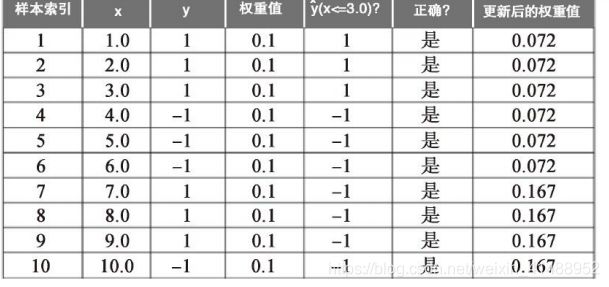
表格的第1列为样本的索引序号，为1〜10。假设此表格代表了⼀个⼀维的数据集，第2列就相当于单个样本的值。第3列是对应于训练样本xi的真实类标yi，其中yi∈{1,-1}。第4列为样本的初始权重，权重值相等，且通过归⼀化使其和为1。在训练样本数量为10的情况下，我们将权重向量w中的权值wi都设定为0.1。假定我们的划分标准为x≤0.3，第5列存储了预测类标 。基于前⾯伪码给出的权重更新规则，最后⼀列存储了更新后的权重值。
乍⼀看，权重更新的计算似乎有些复杂，我们来逐步讲解计算过程。
⾸先计算第5步中权重的错误率：

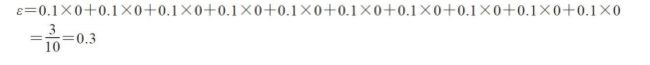
下⾯来计算相关系数αj（第6步），该系数将在第7步权重更新及最后⼀个步骤多数投票预测中作为权重来使⽤。
在计算得到相关系数αj后，我们可根据下述公式更新权重向量：
由此，对于分类正确的样本，其对应的权重在下⼀轮boosting中将从初始的0.1降为0.066/0.914≈0.072。同样，对于分类错误的样本，其对应权重将从0.1提⾼到0.153/0.914≈0.167。
简⽽⾔之，这就是AdaBoost。

小结

在本章的开始，我们⽤Python实现了⼀个MajorityVoteClassifier类，它可以通过组合不同的算法得到⼀个分类器。进⽽我们学习了bagging，它能够在训练集上通过bootstrap进⾏随机抽样，并以多数投票为准则组合多个单独训练的成员分类器，成为⼀种能够有效降低模型⽅差的模型。然后我们讨论了AdaBoost，它是⼀种基于弱学习机的算法，能够从前⼀个弱学习机错误中进⾏学习。