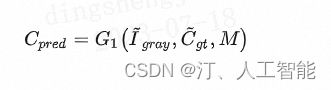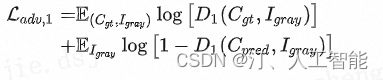图片修补 EdgeConnect 论文的阅读与翻译：生成边缘轮廓先验，再填补缺失内容

本文将要介绍的论文就是：EdgeConnect: Generative Image Inpainting with Adversarial Edge Learning，因为知乎在（2019-02-02）前，缺少详细介绍这篇论文的文章，而我最近需要复现它，所以顺便在这里对这篇论文进行介绍，毕竟还是中文母语阅读起来方便，关于翻译或者算法的指正与争议。

翻译声明

• hallucinating edges 边缘假想图 （通过不完整的图片，生成假想的边缘轮廓图片）
• edges 边缘、轮廓（在出现歧义的情况下，我会将「边缘」翻译成「轮廓」）
• edge detection 边缘检测算法（由于大家都翻译成「边缘检测」）
• image Completion /inpainting 图片修补
• fill the missing regions 填补缺失区域（为包含 修补 之思，故不将 fill 译为 填充）
• ground truth image 真实图片 （我无法给出好的翻译）
• mask 掩膜 （采用的是 PhotoShop 的翻译）

0. 摘要

过去几年，深度学习技术在图片修补领域上取得了显著的成果。然而，这些技术在无法重构出（图片缺失区域的）合理结构，它们总是得到过于平滑或者模糊的结果。这篇论文开发了一种新的图片修补技术，它的修补效果更好，填补的区域展示出了更加精致的细节。我们提出的二阶段图片修补对抗模型 EdgeConnect，整合了边缘生成器与图片修补网络。先由边缘生成器生成出不规则缺失区域的边缘假想图，作为先验结果，然后在这张边缘假想图的基础上，使用图片修补网络对缺失区域进行填充。我们在可获取到的公共数据集 CelebA，Places2，以及 Paris StreetView 上对我们的模型进行端到端的评估，结果表明我们的结果在定量与定性的分析上，优于现阶段的其他算法。

1. 介绍

图片修补 (Image Completion /Inpainting) 就是将一张图片中的缺失区域进行修补。是许多图片编辑任务中的重要一步。举例说明，它可以被应用在 将图片中某个物体移除后，对缺失区域的修补任务上。人类有一种不可思议的能力去消除视觉上的不连续性 (visual inconsistencies)。因而填补区域必须在感知上合理 (be perceptually plausible)。另外，填补区域缺乏精细结构一直是一个令人不快的附属品，尤其是图片中的区域包含锐利的细节时。我们观察到现有图像修复技术会产生过度平滑或者模糊的区域，这推动了本文所介绍的方法的产生。

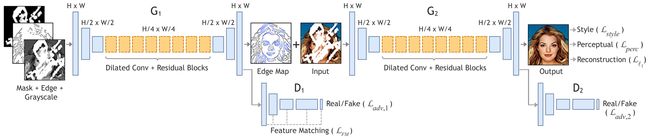
我们将图片修补分为两个阶段（如图 1）：轮廓生成与图片修补。

1. 边缘轮廓生成只关注生成缺失区域中的假想边缘轮廓。
2. 图片修补网络使用轮廓假想图，以及输入的不完整图片，对缺失区域的 RGB 像素数值进行估计。

为了确保生成的边缘假想图 (hallucinated edges) 与 填补区域的 RGB 像素值 (RGB pixel intensities) 在视觉上的感受是连续的 (visually consistent)，这两个阶段的任务，我们都使用了对抗网络去完成。两个网络都包含了基于深度特征的损失函数，以生成尽可能逼真的图片 (enforce perceptually realistic results)。

像大部分计算机视觉问题一样，图片修补任务比深度学习技术更早地被广泛地使用。广义上讲，传统的图片修补方法可以分为两种：扩散型 (diffusion-based) 与 补丁型 (patch-based)。。。。

省略对 扩散型 (diffusion-based) 与 补丁型 (patch-based) 的解释，你们『望文生义』或者『顾名思义』就行了。

目前的深度学习方法在图片修补任务上取得了显著的成果。这些方案通过学习数据的分布对缺失的像素进行填补。他们可以生成缺失区域内连贯的结构。这是传统的技术几乎不可能实现的创举。虽然这些方法可以为缺失区域生成有意义的结构，但是生成的区域通常是模糊图像，或者（不自然的）伪像 (suffer from artifacts)，这表明了这些方法无法准确地重建高频率的信息。

然后，要怎样才能促使图片修补网络生成精致的细节？在图片的结构可以很好地使用它的边缘图片进行表示的情况下，我们（的研究工作）表明了：对图片修补网络进行调整，在缺失区域上生成（轮廓图 作为）先验结果是可行的。显然，我们无法获取缺失区域的边缘。相反，我们可以训练一个轮廓生成器，利用它生成这些缺失区域的轮廓。我们 “生成轮廓线条，在生成填充色彩” 的方案，有一部分灵感来自于艺术家的工作过程。。。。（省略艺术家 Betty Edwards 的话）。。。他从艺术的角度强调了草图的重要性。我们认为轮廓恢复是图片修补中的一项简单的任务，我们提出的模型，在实质上解耦合了图片修补过程中 对缺失区域的 高频与低频信息的恢复过程。

我们在标准的数据集 CelebA，Places2，以及 Paris Sreet View 上进行评估。我们将我们的模型的性能与目前最好的方案进行比较。我们提供了实验囧过来研究边缘信息对图片修补任务的影响。我们的文章做出了以下贡献：

• 一个可以生成（缺失区域）的假想轮廓的边缘轮廓生成器。它在给定了 图片剩余部分的灰度图 的情况下，能够给出缺失区域的轮廓假想图。
• 一个图片修补网络，它可以结合缺失区域（作为先验）的假想轮廓图，根据图片的其余部分，对缺失区域的色彩以及上下文信息进行填补。
• 一个结合了轮廓生成器与图片修补的端到端的训练网络。可以为为缺失区域填补上具有精致细节的内容。

我们展示了我们我们在一下常见的图像编辑任务上的应用，如物体的移除和场景生成任务。我们在 GitHub 上面开源我们的代码： knazeri/edge-connect

2. 相关工作（略写）

• 基于扩散的图片修补算法：根据临近像素，猜测缺失像素，无法得到有意义的结构。
• 基于补丁的图片修补算法：对临近区域进行复制，得到补丁，一块块填补到缺失区域。
• 基于深度学习图片修补算法：发表于 2016 年上下文编码器 context encoder 是首个，etc
• 由图片生成边缘轮廓（边缘检测算法）：Canny Edge detector，Holistically-Nested Edge Detection （使用全卷积网络）
• 由轮廓生成图片：pix2pix（成对的监督训练），CycleGAN（不需要成对的两类图片）

译者注：
如果对于 Context Encoder 感兴趣，可以看 Context Encoders 论文的阅读与翻译
如果对于 CycleGAN 感兴趣，可以看曾伊言：CycleGAN 论文的阅读与翻译
被 EdgeConnect 超越的算法 （图片修补的部分卷积算法）Partial Convolutions (Pconv)。已经有介绍的文章：rootxuan：Image Inpainting for Irregular Holes Using Partial Convolutions 翻译

3. 解决方案 EdgeConnect

我们提出一个图片修补网络，它由两个阶段组成，如上图：

1. 轮廓生成器
2. 图片修补网络

两个阶段都使用了对抗网络如下：

• 生成器使用了与 Johnson 的实时风格迁移 “Perceptual losses for real-time style transfer and super-resolution” 相似的网络架构，这个架构常用于 图片到图片的翻译任务上，如：风格迁移，超分辨率 等。。。。（省略网络架构具体细节）。。。
• 判别器使用了 70x70 的 PatchGAN，也就是将判别图片分成 70x70 进行判别，对判别结果取平均。
• 整个网络的都使用了实例正则化 (instance normalization)

3.1. 轮廓生成器 Edge Generator

• $I_{gt}$ Ground truth 真实图片
• $I_{gray}$ grayscale 真实图片的灰度图
• $C_{gt}$ Canny edge map (ground truth) 真实图片的轮廓图
• $M$ pre-condition mask 先决条件掩膜层（把缺失区域标记为 1，背景图片标记为 0）
• $G_1$ generator_1 轮廓假想图的生成器
• $\odot$ Hadamard product 哈达玛积（矩阵对应位置相乘）

将缺失的区域删除，并用字符上的波浪线标记：

• ${\tilde{I}}_{gray}=I_{gray}\odot (1-M)$不完整的灰度图
• ${\tilde{C}}_{gt}=C_{gt}\odot (1-M)$ 不完整的轮廓图。
• $C_{pred}$ C_{pred} ，predict Canny edges，它是轮廓假想图生成器的预测结果：

构建损失函数如下，用以训练这个对抗网络，得到轮廓生成器 Edge Generator。

${\mathcal{L}}_{adv,1}$，对抗损失（上方的公式中括号与原文位置稍有不同）

${\mathcal{L}}_{FM}=\mathbb{E}[\sum _{i=1}^L\frac{1}{N_i}||D_1^{(i)}(C_{gt}-D_1^{(i)}(C_{pred})|{|}_1]$

${\mathcal{L}}_{FM}$\mathcal{L}_{FM} feature map loss，特征损失，使用预训练好的 VGG 网络对输入的图片进行判别，这里的方法类似于 PatchGAN。注意，由于 VGG 并不是被训练用作提取图像的轮廓边缘的网络，所以此处我们不能直接使用 VGG 的结果。我们用 $L$L 表示判别器的最后一层卷积层。 $N_i$N_i 是判别器的第 $i$i 层的激活结果 (the activation in the $i$i 'th layer of the discriminator)。

用结合了对抗损失，与特征匹配损失 的轮廓判别器对轮廓图片进行判别：$$\begin{gathered} \underset{G_1}{\min }\underset{D_1}{\max }{\mathcal{L}}_{G_1}=\underset{G_1}{\min }({\lambda }_{adv,1}\underset{D_1}{\max }({\mathcal{L}}_{adv},1)+{\lambda }_{FM}{\mathcal{L}}_{FM}) \\ {\lambda }_{adv,1}=1,{\lambda }_{FM}=10 \end{gathered}$$

译者注：
原先的图片修补任务需要对 RGB 值图片的缺失区域进行修补，如果采用范数距离计算重构损失 ${\mathcal{L}}_{reconstruction}$的话，总得到模糊的图片（对可能的修补模式求平均的结果）；如果采用特征距离计算对抗损失 ${\mathcal{L}}_{adversarial}$的话，总得到人造痕迹太明显的图片（伪像）（从训练记忆里面找一个相似的结果并贴上去）。上下文编码器 Context Encoder 采用参数加权的方式结合使用两者，只是平衡了这两个缺点。
既然如此，把图片修补任务的难度降低，不修复三通道的 RGB 图，转而修复只有轮廓的二值图。修复得到了轮廓图片后，将其转变为风格迁移任务（将轮廓图转化为彩色图片）。这个过程，把恢复高频信息与低频信息的过程解耦合，从而解决图片修补任务。

此外，使用 谱归一化 (Spectral Normalization, SN) 稳定判别器的训练。

译者注： 谱归一化是 WGAN 的简化。
何为 WGAN（Wasserstein GAN）？
引入 Wasserstein Distance 使得判别器满足 **限制导数小于 K 的 L 连续（K-Lipschitz continuous）**的条件。这个方案认为：训练过程中，判别器过早进入了理想状态，总是很好地识别真实数据，此时如果两个分布距离很远，几乎没有重叠，那么 KL 散度（KL Divergence）或者 JS 散度 几乎无法给生成器提供梯度信息。因此，即便在两个分布没有重叠的时候，使用 Wasserstein Distance（推土机距离）正确地度量两个分布的距离，将会使判别器更稳定地为生成器提供梯度。
何为谱归一化 (Spectral Normalization, SN)？
求解 Wasserstein Distance 的计算量较大：通过对权重的奇异值求解，可以得到这一层网络的谱范数（spectral norm），接着让每一层网络的权重除以这一层网络的谱范数就可以满足 1-Lipschitz continuous。因此我们采用幂函数迭代法（power iteration）近似地求解谱范数。

3.2. 图片修补网络 Image Completion Network

$C_{comp}=C_{gt}\odot (1-M)+C_{pred}\odot M$C，composite，合成轮廓图

$I_{pred}$，它是图片修补网络的预测结果：

$I_{\text{pred }}=G_2\left({\tilde{I}}_{gt},C_{\text{comp }}\right)$

构建损失函数如下，用以训练这个对抗网络，得到轮廓生成器 Edge Generator。

$\begin{array}{rl}{\mathcal{L}}_{adv,2}& ={\mathbb{E}}_{\left(I_{gt},C_{\text{comp }}\right)}\log \left[D_2\left(I_{\text{gt }},C_{\text{comp }}\right)\right]\\ & +{\mathbb{E}}_{C_{\text{comp }}}\log \left[1-D_2\left(I_{\text{pred }},C_{\text{cornp }}\right)\right]\end{array}$

${\mathcal{L}}_{adv,2}$ adversarial loss，对抗损失（上方的公式中括号与原文位置稍有不同）

${\mathcal{L}}_{prec}=\mathbb{E}[\sum _i\frac{1}{N_i}||{\varphi }_1^{(i)}(I_{gt}-{\varphi }_1^{(i)}(I_{pred})|{|}_1]$

${\mathcal{L}}_{prec}$ preceptual loss，感知损失，使用预训练好的 VGG-19 网络对输入的图片进行判别，参见 PatchGAN。公式中的 ${\varphi }_i$ 对应了来自 VGG-19 的激活函数特征图 $relu\_i\_1$ , 其中 $i\in \{1,2,3,4,5\}$ 。VGG-19 网络来自在 ImageNet 上的预训练版本。

${\mathcal{L}}_{style}={\mathbb{E}}_j[||G_j^{\varphi }(I_{pred})-G_j^{\varphi }(I_{gt})|{|}_1]$

${\mathcal{L}}_{style}$ style loss 风格损失。公式中的 $G_j^{\varphi }$是一个 $C_j\times C_j$的伽马矩阵 (Gram Matrix) 对激活函数特征图 ${\varphi }_j$ 进行构造得到的，我们使用的风格损失函数，在 Sajjadi 的论文 Single image super-resolution through automated texture synthesis 得到叙述。

用结合了绝对值范数（L1 距离 ${\ell }_1$ ），对抗损失，感知损失，以及风格损失的轮廓判别器对轮廓图片进行判别：

$$\begin{gathered} {\mathcal{L}}_{G_2}={\lambda }_{{\ell }_1}{\mathcal{L}}_{{\ell }_1}+{\lambda }_{adv,2}{\mathcal{L}}_{adv,2}+{\lambda }_p{\mathcal{L}}_{perc}+{\lambda }_s{\mathcal{L}}_{style} \\ {\lambda }_{{\ell }_1}=1,{\lambda }_{adv,2}={\lambda }_p=0.1,{\lambda }_{style}=250 \end{gathered}$$

译者注：可以写成与 Edge Generator 部分相对称的形式，同样有：
$$\begin{gathered} \underset{G_1}{\min }\underset{D_1}{\max }{\mathcal{L}}_{G_1}=({\lambda }_{{\ell }_1}{\mathcal{L}}_{{\ell }_1}+{\lambda }_{adv,2}\underset{D_1}{\max }({\mathcal{L}}_{adv,2})+{\lambda }_p{\mathcal{L}}_{perc}+{\lambda }_s{\mathcal{L}}_{style}) \\ {\lambda }_{{\ell }_1}=1,{\lambda }_{adv,2}={\lambda }_p=0.1,{\lambda }_{style}=250 \end{gathered}$$

4. 实验部分

4.1. 轮廓信息与图片掩膜层

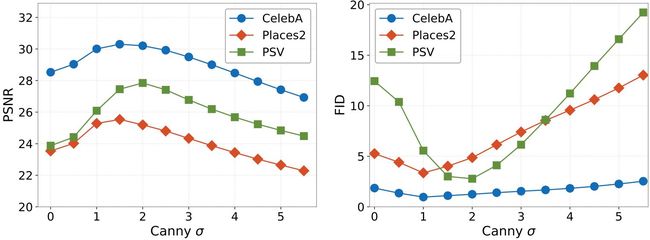
使用 Canny 边缘（轮廓）检测算法，得到轮廓二值图，然后使用高斯模糊对轮廓图片进行处理，发现当高斯模糊的参数 $\sigma \approx 2$的时候，恢复效果最好。。。省略测试详细内容。。。

4.2 训练设置与训练策略

使用 PyTorch，图片尺寸为 256x256，批次大小为 8，使用 Adam optimizer（ ${\beta }_1=0,{\beta }_2=0.9$）。

$G_1$使用 Canny 边缘轮廓检测算法，在学习率为 $10^{-4}$ 下进行训练，直到损失下降到平坦表面 (until the losses plateau)。接着修改学习率为 $10^{-5}$，同时对 $G_1,G_2$ 进行训练，直到收敛。最终，我们将 $D_1$移除，然后在学习率为 $10^{-6}$下，对 $G_1,G_2$ 进行端到端的训练，直到收敛。判别器的学习率为生成器的十分之一。

5. 结果（省略）

5.1 定性的分析（省略了论文对比较结果的点评与分析）

5.2 定量的分析（省略了论文对比较结果的点评与分析）

使用了四个对比指标：

• ${\ell }_1$ 范数 Norm (mathematics) - Wikipedia (Absolute-value norm)
• FID Fréchet Inception Distance - 知乎 尹相楠
• SSIM 结构相似性 Structural SIMilarity - Wikipedia
• PSNR 信噪比 Peak Signal-to-Noise Ratio - Wikipedia

参与比较方法，如下：

• CA Contextual Attention
• GLCIC Globally and Locally Consistent Image Completion
• PConv Partial Convolution （NVIDIA 的部分卷积）
• EdgeConnect （这篇论文的方法）
• EdgeConnect with Canny Edges Priori （将 Canny 边缘轮廓检测图作为先验）

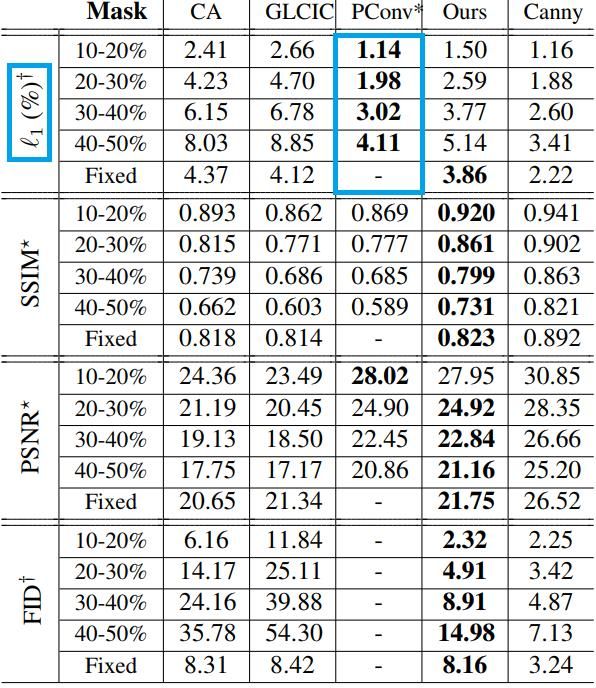
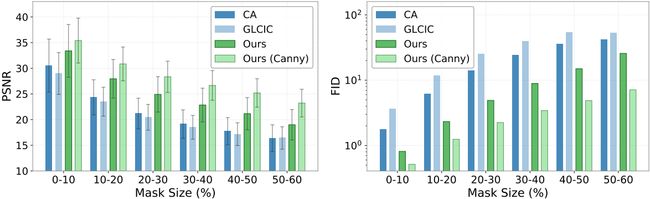
对比结果如下方表格 1，与下方图 5。

我的看法：值得注意的是表格 1 中蓝色方框的内容，尽管对于 L1 范数指标，PConv 要高于此论文的 EdgeConnect 方法，但是这并不意味着在 L1 范数指标下 这篇论文的方法不如 PConv。相反的，结合这张表格给出的其他指标，EdgeConnect 总体来说要优于 PConv，这使得 L1 范数的对比结果，反而从侧面佐证了 EdgeConnect 产生的结果要比 PConv 的结果更加清晰 的观点。
某些的神经网络 使用了 L1 范数作为图像重构，并搭配上其他损失 直接对生成器进行优化，可能是导致生成的图片模糊的原因（Context Encoder 的论文里面分析过这个问题），想看这篇论文的话，点击此处→ Context Encoders 论文的阅读与翻译，然后 Ctrl +F 定位到关键字 “安全”“预测缺失值的平均分布是更加 “安全” 的做法” 用于评价重构损失的这句话。

**视觉图灵测试 Visual Turing Tests（略）**让人类作为判别器，评估图片生成效果。

5.3 模型简化测试 Ablation Study（略）

完整的模型 与 删去轮廓假想图的模型（略）（其实相当于下一行的 Canny 边缘轮廓检测算法，输出空白的轮廓图片的情况）

使用 Canny 边缘检测算法，在不同的 $\sigma$\sigma 值下，产生不同的边缘轮廓进行比较，如下方图 7，结论是当 \sigma 减少到 3（边缘数量增加到某个程度的时候），生成图片的效果不再增强。

更换边缘轮廓检测（算法）系统，如图 8，结论是 我们没有得到明显的差异。

• Canny Edges Detection Algorithm， Canny 边缘检测算法（被 OpenCV 收录的经典算法）
• Holistically-Nested Edge Detection (HDE)，整体 - 邻域 边缘检测系统（一个全卷积网络）

6. 讨论与未来的工作（省略）

我的看法：恢复的结果，比如上面的狗，我们人类可能根据拴着的链子，能先判断它可能是狗，再从脑海中想象出一个狗头，最后脑补上去。而这机器恢复的图片，小图看起来像是猫（因为它没有尖尖的嘴巴）。另外受到神秘东方力量影响的单个黑框眼镜，与不符合牛顿力学的金拱门，以及有点抽象派画风的侧脸（可能是打网球的德约科维奇吧）。
现在还不能简单地说这些图片恢复得不好，而是因为这些图恢复得过于奇幻了。可能是因为机器缺乏人类常识才造成了这种违和感。

关**于缺乏人类常识（例如某种语言的单词）**的机器恢复效果分析。
第一个例子，L→I，看来这是在没有学过英字母的情况下，比较合理的恢复了。而作为人类的我在具备人类常识的情况下，能够猜测出这个单词是 HOTEL，做到正确脑补。第二个例子，它是上下文编码器里面用到的一幅图片，里面的服装店名字是 la bonne accroche，在没有学过法语的情况下（比如我），也和机器一样无法正确恢复出来。
看来现阶段，影响图片修补结果质量的一部分因素，就是 “缺乏人类常识了”。

另外，可以用它做风格迁移。

图 A 与图 B 画风不同。保留 A 图的左半图，选择 B 图的右半图进行边缘检测，得到边缘 B 右半图，这样就能得到拥有风格 B 的结构，风格 A 的画风，的右半图了，如下方图 10。

我的看法：其实可以实现完整的风格迁移，将上面的过程，照着右半图重复一遍，就能得到将以 B 图为骨架（边缘轮廓），以 A 图为画风的图片。图 10 中的第五列图片 A 画风与 B 边缘，不是论文原文的内容 ，而是我选取第四列的右半图，进行水平翻转后得到左半图，与原始右半图拼合得到的图片。本来的操作应该是以 A 图右半图的画风，加上 B 图左半图的轮廓，得到左半图的画面才对，但是现在我还没有时间复现这篇论文。

还可以做许多事情，如下方图 11：

• 物体移除（广义上的大神帮我把某物 P 掉）
• 物体调整（广义上的大神帮我把某物 P 好看点）

附录（省略）

A. 网络架构

1. 生成器
2. 判别器

B. 实验结果（数据集）

1. 边缘生成器准确度
2. 完整的结果
3. 其他的边缘检测系统的结果

代码中的 model123，其中 model 3 是端到端的进行训练的吗，还有 joint model 和 model3 有什么区别？

文章训练了两个网络，分别是 3.1. Edge Generator 以及 3.2. Image Completion Network。分别 这两个网络的训练后，会将这两个网络连接起来，组成完整的网络进行联合训练。文章中的 4.2. Training Setup and Strategy 详细记录了训练流程。

破损图像是怎么生成的呢?

「生成随机掩膜层」论文原文似乎没有提供随机生成图片删去区域的算法，再加上私信问我的人太多了，几乎是点赞数量的一半。所以由我来提供这个算法： Github Yonv，生成随机的掩膜层 DEMO_generate_random_mask.py。运行效果如图：

算法原理是：使用三个点确定贝塞尔曲线，然后在生成的曲线上绘制大小变化的圆形，从而得到连续的随机区域（Mask：保留区域赋值为 1，删除区域为 0）。Image * Mask 得到破损图片。当然，你可以将圆形笔触调整为矩形获得其他风格的缺失区域，也可以调整笔触的绘画间隔，牺牲笔触效果用以追求极致的程序运行速度。