PAT(甲级)2022年夏季考试
7-1 What Day is Today(20分)
Amy and Tom are arguing about what day is today. Their conversations are as the following:
Amy: Today is Friday.
Tom: No! Today is Saturday.
Amy: But Wednesday was yesterday.
Tom: No way! Yesterday was Thursday.
Amy: Then tomorrow must be Tuesday.
Tom: Are you kidding? It's Monday tomorrow.
Now their mother tells you that each of them has said only one thing correct. It's your job to tell exactly what day is today.
Input Specification:
Each input file contains one test case. Each case consists of 2 lines, each gives the claims of a kid, in the following format:
yesterday today tomorrow
where the days are represented by numbers from 0 to 6, corresponding to Sunday through Saturday.
Output Specification:
First output in a line the English name for "today". It is guaranteed that each kid has said only one thing correct, and there is a unique answer for "today".
Then in the next two lines, print in order the correct days (either yesterday or today, or tomorrow) obtained from the kids.
Sample Input:
3 5 2
4 6 1
Sample Output:
Friday
today
yesterday
Note: The English names for the days are
0 - Sunday
1 - Monday
2 - Tuesday
3 - Wednesday
4 - Thursday
5 - Friday
6 - Saturday代码(Python3):
pre = [6, 0, 1, 2, 3, 4, 5]
next = [1, 2, 3, 4, 5, 6, 0]
day = ["yesterday", "today", "tomorrow"]
week = ["Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"]
a = list(map(int, input().split()))
b = list(map(int, input().split()))
for i in range(7):
c1 = 0
c2 = 0
if a[0] == pre[i]:
c1 += 1
r1 = 0
if a[1] == i:
c1 += 1
r1 = 1
if a[2] == next[i]:
c1 += 1
r1 = 2
if b[0] == pre[i]:
c2 += 1
r2 = 0
if b[1] == i:
c2 += 1
r2 = 1
if b[2] == next[i]:
c2 += 1
r2 = 2
if c1 == 1 and c2 == 1:
print(week[i])
print(day[r1])
print(day[r2])
break
7-2 Least Recently Used Cache(25分)
Least Recently Used (LRU) cache scheme is to remove the least recently used frame (the one hasn't been used for the longest amount of time) when the cache is full and a new page is referenced which is not there in cache.
Your job is to implement this LRU cache scheme.
Input Specification:
Each input file contains one test case. For each case, the first line gives 2 positive integers N (≤104) and M (≤105) which are the size of the cache and the number of referenced page ID's. Then M referenced page ID's are given in the next line. A page ID is a number in the range [1,2×104]. All the numbers in a line are separated by a space.
Output Specification:
For each test case, output in a line the page ID's in the order of their being removed from the cache. All the numbers in a line must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.
It is guaranteed that at least one page will be removed.
Sample Input:
4 11
1 2 3 1 4 5 2 1 5 6 3
Sample Output:
2 3 4 2
Hint:
When pages with ID's 1, 2, and 3 comes in order, they are all stored in the cache and page 1 is now the LRU frame.
When page 1 is accessed, page 2 then becomes the LRU frame.
Page 4 can still be stored in the cache, and now the cache is full. When page 5 is to be cached, page 2 will be removed and page 3 becomes the LRU frame.
When the next page 2 comes in, page 3 is removed and page 1 becomes the LRU frame.
Then page 1 is accessed, so page 4 becomes the LRU frame.
When page 5 is accessed, the LRU frame is not changed. Then page 6 comes in and page 4 is removed. The LRU frame is now page 2.
Finally page 2 is removed when page 3 comes in.
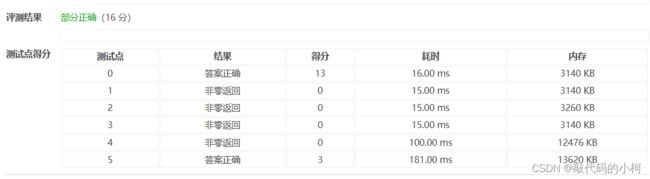
提交结果:
代码(Python3):
n, m = list(map(int, input().split()))
data2 = list(map(int, input().split()))
c = 0
q = []
num = {}
v = []
r = []
for x in data2:
num[x] = 0
for x in data2:
if c < n:
q.append(x)
if num[x] == 0:
c += 1
num[x] += 1
else:
if num[x] == 0:
while num[q[0]] != 1:
num[q[0]] -= 1
q.pop(0)
num[q[0]] -= 1
r.append(str(q[0]))
q.pop(0)
q.append(x)
num[x] += 1
print(" ".join(r))
7-3 DFS Sequence(25分)
The above question is commonly seen in a final exam of the course Data Structures. That is, given a graph G, you are supposed to tell if a sequence of vertices can be possibly obtained from any depth first search (DFS) on G.
Now it is your job to write a program which can give the answers automatically.
Note: it is required that each vertex must be visited once even if the graph is not connected. In the graph given by the sample input, if we start from vertex 4, then vertex 1 cannot be reached during this DFS, yet it can be the first vertex visited in the next DFS. Hence the 5th query 4 3 2 5 1 is possible.
Input Specification:
Each input file contains one test case. For each case, the first line contains 3 positive integers: N (≤103), M (≤104), and K (≤100), which are the number of vertices, the number of edges, and the number of queries, respectively. Then M lines follow, each gives an edge in the format:
source destination
which means that there is an edge from source vertex to destination vertex. Here we assume that all the vertices are numbered from 1 to N. It is guaranteed that source is never the same as destination.
Finally K lines of queries are given, each contains N vertices. The numbers in a line are separated by spaces.
Output Specification:
For each query, print in a line yes if the given sequence does correspond to a DFS sequence, or no if not.
Sample Input:
5 7 6
1 2
1 3
1 5
2 5
3 2
4 3
5 4
1 5 4 3 2
1 3 2 5 4
1 2 5 4 3
1 2 3 4 5
4 3 2 5 1
5 4 3 2 5
Sample Output:
yes
yes
yes
no
yes
no提交结果:
代码(Python3):
def dfs(x):
global flag
if flag == 0 or q == []:
return
vis[x] = 1
while q != []:
if a[x - 1][q[0] - 1] == 1:
y = q[0]
q.pop(0)
dfs(y)
else:
for i in range(len(vec[x])):
if vis[vec[x][i]] == 0:
flag = 0
return
return
vis = {}
vec = {}
n, m, k = list(map(int, input().split()))
a = [[0 for j in range(n)] for i in range(n)]
for i in range(m):
x, y = list(map(int, input().split()))
a[x - 1][y - 1] = 1
if x not in vec.keys():
vec[x] = [y]
else:
vec[x].append(y)
for i in range(k):
flag = 1
q = list(map(int, input().split()))
s = set(q)
for x in q:
vis[x] = 0
while q != []:
y = q[0]
q.pop(0)
dfs(y)
if flag == 0 or len(s) != n:
print("no")
else:
print("yes")
7-4 Complete D-Tree(30分)
A d-tree is a tree of degree d. A complete tree is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.
Given the pre-order traversal sequence of a complete d-tree, you are supposed to obtain its level-order traversal sequence. And more, for any given node, you must be able to output the bottom-up path from this node to the root.
Input Specification:
Each input file contains one test case. For each case, the first line gives two positive integers: N (≤50) and d (2≤d≤5), which are the total number of nodes in the tree, and the tree's degree, respectively. Then in the next line, N integer keys (≤100) are given as the pre-order traversal sequence of the tree. Finally K (≤N) and K positions are given, where each position is the index of a key in the level-order traversal sequence, starting from 0.
All the numbers in a line are separated by a space.
Output Specification:
For each case, first print in one line the level-order traversal sequence of the complete d-tree. Then for each given position, print in a line the bottom-up path from this node to the root.
All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line.
Sample Input:
9 3
91 71 2 34 10 15 55 18 7
3
5 7 3
Sample Output:
91 71 15 7 2 34 10 55 18
34 71 91
55 15 91
7 91代码(Python3):
def dfs(x):
if x >= n:
return
le[x] = pre[0]
pre.pop(0)
for i in range(1, d + 1):
dfs(x * d + i)
le = {}
n, d = list(map(int, input().split()))
pre = list(map(int, input().split()))
dfs(0)
for i in range(n):
print(le[i], end="")
if i < n - 1:
print(" ", end="")
else:
print()
k = int(input())
data = list(map(int, input().split()))
for x in data:
while x:
print(le[x], end=" ")
x = int((x - 1) / d)
print(le[0])