Python数码管之十进制转十六进制

首先呢，问题如下：

上面这个图是符号的数码管显示

 问题是这个：

 因为转十六进制，会存在字母ABCDEF代表10-15，还有一个就是，需要D和H用来在旁边表示进制符号,就是如下这样

 

思路：

思路非常简单，就是先进行十进制转16进制，直接取余数，储存起来，然后直接倒序过来就是该十进制数的十六进制了，

具体代码就是这样的：

       

def jinzhi(a):
    i=0
    b={}
    while a!=0:
        b[i]=str(int(a%16))
        if b[i]=='10':
            b[i]='A'
        if b[i]=='11':
            b[i]='B'
        if b[i]=='12':
            b[i]='C'
        if b[i]=='13':
            b[i]='D'
        if b[i]=='14':
            b[i]='E'
        if b[i]=='15':
            b[i]='F'
        a=int(a/16)
        i=i+1

    b1={}
    c=0
    d=len(b)
    d=d-1
    print(b)#检验一下b，你们删掉也可以的
    while 1:
        b1[c]=b[d]
        if b[d]==b[0]:
            break
        c=c+1
        d=d-1
    return b1

你们很容易发现了，我用的是字典类型{},因为列表在里面没有字典那么好，元组是无法修改的，字典还是不错的，

然后呢，就是画图了，首先画的是十进制的，再然后画十六进制

这里我直接给源代码了：

import turtle as t
def jinzhi(a):
    i=0
    b={}
    while a!=0:
        b[i]=str(int(a%16))
        if b[i]=='10':
            b[i]='A'
        if b[i]=='11':
            b[i]='B'
        if b[i]=='12':
            b[i]='C'
        if b[i]=='13':
            b[i]='D'
        if b[i]=='14':
            b[i]='E'
        if b[i]=='15':
            b[i]='F'
        a=int(a/16)
        i=i+1

    b1={}
    c=0
    d=len(b)
    d=d-1
    print(b)#检验b
    while 1:
        b1[c]=b[d]
        if b[d]==b[0]:
            break
        c=c+1
        d=d-1
    return b1

def drawLine(draw):
    t.pendown() if draw else t.penup()
    t.fd(40)
    t.right(90)


def drawDight(d):

    drawLine(True) if d in ['2', '3', '4', '5', '6', '8', '9', 'A', 'B', 'D', 'E', 'F', 'H'] else drawLine(False)
    drawLine(True) if d in ['0', '1', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'D', 'H'] else drawLine(False)
    drawLine(True) if d in ['0', '2', '3', '5', '6', '8', '9', 'B', 'C', 'D', 'E'] else drawLine(False)
    drawLine(True) if d in ['0', '2', '6', '8', 'A', 'B', 'C', 'D', 'E', 'F', 'H'] else drawLine(False)
    t.left(90)
    drawLine(True) if d in ['0', '4', '5', '6', '8', '9', 'A', 'B', 'C', 'E', 'F', 'H'] else drawLine(False)
    drawLine(True) if d in ['0', '2', '3', '5', '6', '7', '8', '9', 'A', 'C', 'E', 'F'] else drawLine(False)
    drawLine(True) if d in ['0', '1', '2', '3', '4', '7', '8', '9', 'A', 'D', 'H'] else drawLine(False)
    t.left(180)
    t.penup()
    t.fd(20)
def ggg(a,p):
    i=0
    if p==16:
        while i

main函数可能会有点复杂，其实就是画完十进制，然后把海龟下一行，并且稍微跟第一行对准一下，然后继续输出十六进制，中途就是颜色的变化。

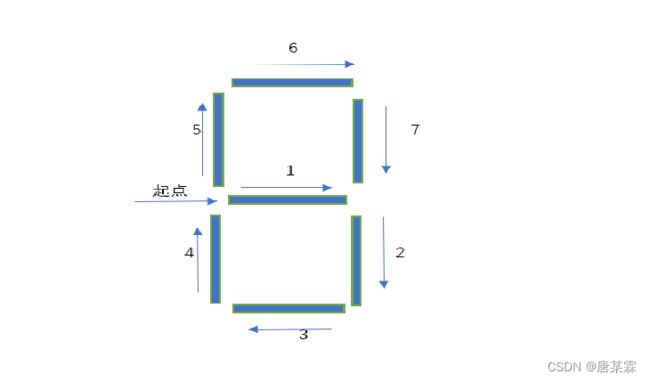
drawDight这个函数的作用是,通过ggg这个函数传输过来的字符进行判断,是否符合那些列表里面的数，一共是七次判断是否属于该列表里面的数，七次，其实就是对应七段数码管

了解这个图的话，应该就可以了解这七句判断了

 先看这个图，其实方向可以自定义的，我用的这个方向是教材里面的，大家都可以接受。

每一句话都代表着一个画图的指令，最上面有个表，就是对每一个数的数码管，哪一条管可以画，哪一条管不可以画，这样就组成了一个数的数码管

学会了吗0.0