递归的理解与应用（详细）

一、▶️什么是递归

1.1函数递归的定义

递归*** 程序调用自身的编程技巧称为递归

1.2函数递归的优缺点

优点：简化代码，大量的重复性过程被简化，“大事化小”的编程思想 。
缺点： 1. 执行效率慢，以为每次调用都会在栈区开辟一块空间，也就是压栈。
2.如果递归次数太多，会造成 栈溢出问题，（栈区大小：2M或1M。函数内申请的变量、数组，是在栈（stack）中申请的一段连续的空间。）比如求 斐波拉契问题数值过大后造成栈溢出。

1.3函数递归的两个必要条件

1.存在限制条件，当满足这个限制条件的时候，递归便不再继续。
2.每次递归调用之后越来越接近这个限制条件

二. 递归入门（通过一道例题）

打印整数每一位
题目要求：接收一个整型值（无符号），按照顺序打印它的每一位。
例如：
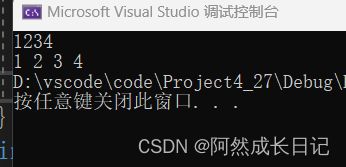
输入：1234，输出 1234

2.1思路分析

解题思路：这种输入输出数字的题，我们一定要想到取模和取余的方法,
并且要有限制条件，每次函数递归后，都会越来越接近这个值。
所以先函数递推1234%10=4,123%10=3,12%10=2,1%10=1，给定限制条件n>9
,直到n=1，最后函数回归打印出1234。

2.2代码

#include
int print(int n) {
	if (n > 9) {
		print(n / 10); //每次缩小一位
	}
	printf("%d ", n % 10);//打印最后一位数
}
int main() {
	int n = 0;
	scanf("%d", &n);![在这里插入图片描述](https://img-blog.csdnimg.cn/4cd4680f47f2405fbcb87a70cb6f17f1.png#pic_center)

	print(n);
	return 0;
}

2.2.1 执行结果

2.3递归思路图解

2.4 补充：打印4321

搞懂流程后，逆序打印也变得很好理解，我只需要**先输出后递**即可

2.4.1代码实现

#include
int print(int n) {
	printf("%d ", n % 10);//放在递归函数之前，将先打印
	if (n > 9) {
	  print(n / 10);
	}
	//printf("%d ", n % 10);
}
int main() {
	int n = 0;
	scanf("%d", &n);
	print(n);
	return 0;
}

2.4.2执行结果

三. 函数递归典型例题的实现

这里在写几道题巩固理解

3.1 求n的阶乘

3.1.1题目描述

用递归的方法求n的阶乘（不考虑溢出问题）
例如：
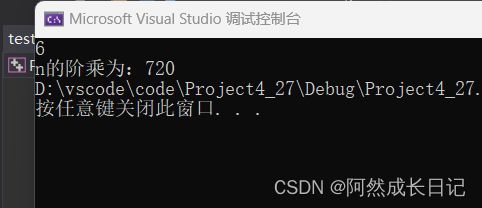
输入：4，输出 24

3.1.2解题思想

n的阶乘为1234…(n-1)n，我们可以先用递推的思想，先算出n(n-1)的值，再用n(n-1)的值乘以(n-2),这样依次乘下去，以n=1为限制条件，返回1。然后再用回归思想，返回回去，及可得到n的阶乘。

3.1.3代码实现

#include
int factorial(int n)
{
	if (n == 1)
		return 1;
	else
		return n * factorial(n - 1);        
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = factorial(n);
	printf("n的阶乘为：%d", ret);
	return 0;
}

3.1.4执行结果

3.1.4递归流程图

3.2strlen函数的模拟实现

3.2.1题目描述:

用递归的方法模拟实现strlen函数
例如：
输入：abc，输出 3

3.2.2 解题思想

strlen函数遇到 ’\0’才会停止，所以我们以 ’\0’为限制条件，我们每调用一次我们自己实现的my_strlen函数，次数就加一，直到遇到 ’\0’停止。

3.2.3 代码实现

int my_strlen(char* str)
{

	if (*str != '\0')
	{
		return 1 + my_strlen(str + 1); //str是数组的首地址
	}
	return 0;
}
int main()
{
	char a[] = "abcdefg";
	int ret = my_strlen(a);
	printf("%d", ret);
	return 0;
}

3.2.4执行结果

3.3求n的k次幂

3.3.1题目描述

用递归的方法实现n的k次幂
例如：
输入：3,3，输出 27

3.3.2解题思路

解题思路：以k>0和k=0为限制条件，每一次递推就乘以n，并且k都减一次1，直到不满足限定条件，然后回归，即为27。

3.3.3代码

#include
int power(int n, int k)
{
	if (k > 1)
	{
		return power(n, k - 1) * n;
	}
	else
		return n;
}

int main()
{
	int n = 0;
	int k = 0;
	scanf("%d", &n);
	scanf("%d", &k);
	int ret = power(n, k);
	printf("%d ", ret);
	return 0;
}

3.3.4执行结果

3.5斐波那契数

3.5.1 题目描述

计算斐波那契数递归实现求第n个斐波那契数
例如：输入：5 输出：5
输入：10， 输出：55

3.5.1 解题思路

斐波那系数是前两项加起来等于后一项：1，1，2，3，5，8，13…,所以我们可以以n<=2为限制条件，当n=1或2时，返回1，然后到n=3项时就是n=1项和n=2项之和，然后依次往后推，即Fib(n)就是Fib(n-1)和Fib(n-2)之和。

3.5.2.1非递归求解

#include
int fac(int n) {
	int a=1, b=1, res=0;
	if (n == 1 || n == 2) {
		return 1;
	}
	else {
		for (int i = 3; i <= n; i++) {
			res = a + b;
			a = b;
			b = res;
		}
	}
	return res;
}
int main() {
	int n;
	scanf("%d", &n);
	printf("%d",fac(n));
	return 0;
}

3.5.2.2执行结果

3.5.3.1递归求解

#include
int fac(int n) {//斐波那契非递归
	int a=1, b=1, res=0;
	if (n == 1 || n == 2) {
		return 1;
	}
	else {
		return fac(n - 1) + fac(n - 2);	
	}
}
int main() {
	int n;
	scanf("%d", &n);
	printf("%d",fac(n));
	return 0;
}

3.5.3.2执行结果

斐波那契数的非递归的实现优于递归实现的原因

1.因为每一次函数递归（函数调用）都会在函数栈帧上开辟一块空间，所谓的压栈。这样会大大降低我们代码的执行效率。
2用递归法实现的斐波那契数正对应了其缺点，因为它的递推时会有很多分支，一个分支下面又有很多分支，每一个小分支都是函数的调用，然而还有回归，函数栈帧需要销毁，这会大大降低代码的执行效率，如果n=50，则代码执行时间都要1个多小时，所以用递归法实现的斐波那系数其实是不实用的。
3.而用非递归的方法实现，可以大大提高代码的运行效率。只是每一次循环，n1,n2,tmp会被赋值，代码执行次数大大减少，所以斐波那契数的非递归的实现优于递归实现的。