KMP 算法推演总结

---

title: KMP 算法推演总结
date: 2023-07-17 16:07:13
tags:

• 算法
  categories:
• 数据结构与算法
  cover: https://cover.png
  feature: false

---

KMP 算法推演

可先见 Fan’s Web 字符串匹配的 BF 算法、RK 算法部分，后面的 BM 算法及 KMP 算法可以搭配一起看

KMP 算法的核心，是一个被称为部分匹配表（Partial Match Table）的数组，先来解释一下 PMT 中的值到底是什么

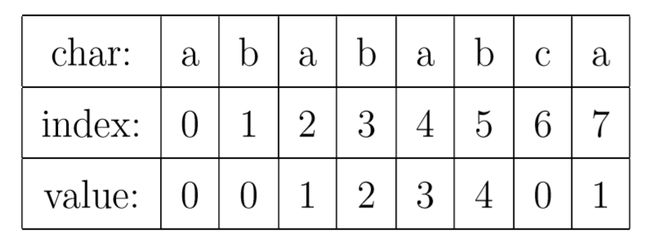
对于字符串“abababca”，它的 PMT 如下表所示：

就像例子中所示的，如果待匹配的模式字符串有 8 个字符，那么 PMT 就会有 8 个值

这里先解释一下字符串的前缀和后缀。如果字符串 A 和 B，存在 A=BS，其中 S 是任意的非空字符串，那就称 B 为 A 的前缀。例如，“Harry”的前缀包括{“H”, “Ha”, “Har”, “Harr”}，我们把所有前缀组成的集合，称为字符串的前缀集合

同样可以定义后缀 A=SB， 其中 S 是任意的非空字符串，那就称 B 为 A 的后缀，例如，“Potter”的后缀包括{“otter”, “tter”, “ter”, “er”, “r”}，然后把所有后缀组成的集合，称为字符串的后缀集合。要注意的是，字符串本身并不是自己的后缀

有了这个定义，就可以说明 PMT 中的值的意义了。PMT 中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。例如，对于“aba”，它的前缀集合为{“a”, “ab”}，后缀集合为{“ba”, “a”}。两个集合的交集为{“a”}，那么长度最长的元素就是字符串“a”了，长度为 1，所以对于“aba”而言，它在 PMT 表中对应的值就是 1。再比如，对于字符串“ababa”，它的前缀集合为{“a”, “ab”, “aba”, “abab”}，它的后缀集合为{“baba”, “aba”, “ba”, “a”}， 两个集合的交集为{“a”, “aba”}，其中最长的元素为“aba”，长度为 3

解释清楚这个表是什么之后，我们再来看如何使用这个表来加速字符串的查找，以及这样用的道理是什么

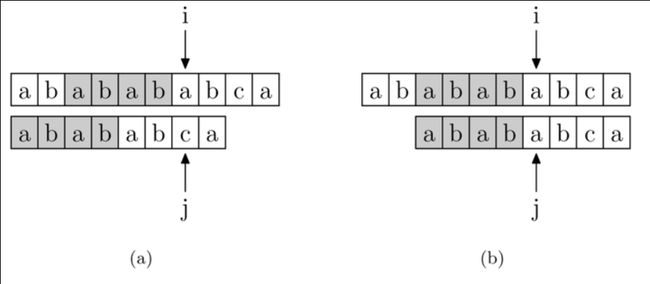
如下图所示，要在主字符串 “ababababca” 中查找模式字符串 “abababca”。如果在 j 处字符不匹配，那么由于前边所说的模式字符串 PMT 的性质，主字符串中 i 指针之前的 PMT[j −1] 位就一定与模式字符串的第 0 位至第 PMT[j−1] 位是相同的。这是因为主字符串在 i 位失配，也就意味着主字符串从 i−j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的

而前面也解释了，模式字符串从 0 到 j−1 ，在这个例子中就是”ababab”，其前缀集合与后缀集合的交集的最长元素为“abab”， 长度为 4。所以就可以断言，主字符串中 i 指针之前的 4 位一定与模式字符串的第 0 位至第 4 位是相同的，即长度为 4 的后缀与前缀相同。这样一来，我们就可以将这些字符段的比较省略掉。具体的做法是，保持 i 指针不动，然后将 j 指针指向模式字符串的 PMT[j −1]位即可

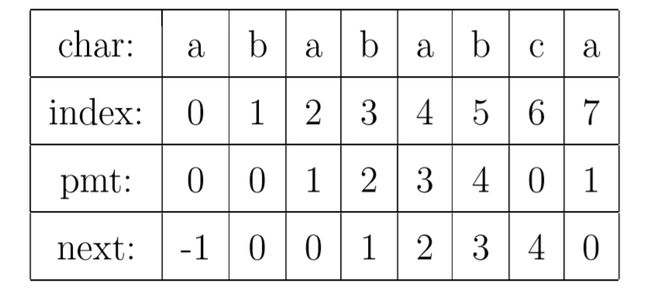
有了上面的思路，我们就可以使用 PMT 加速字符串的查找了。我们看到如果是在 j 位 失配，那么影响 j 指针回溯的位置的其实是第 j −1 位的 PMT 值，所以为了编程的方便， 我们不直接使用 PMT 数组，而是将 PMT 数组向后偏移一位

我们把新得到的这个数组称为 next 数组，如下图所示。其中要注意的一个技巧是，在把 PMT 进行向右偏移时，第 0 位的值，我们将其设成了 -1，这只是为了编程的方便，并没有其他的意义

通过 next 数组进行字符串匹配加速的字符串匹配程序如下：

int KMP(char *t, char *p) {
    int i = 0; 
    int j = 0;

    while (i < (int) strlen(t) && j < (int) strlen(p)) {
	if (j == -1 || t[i] == p[j]) {
            i++;
            j++;
	} else {
            j = next[j];
    	}
    }

    if (j == strlen(p)) {
       return i - j;
    } else {
       return -1;
    }
}

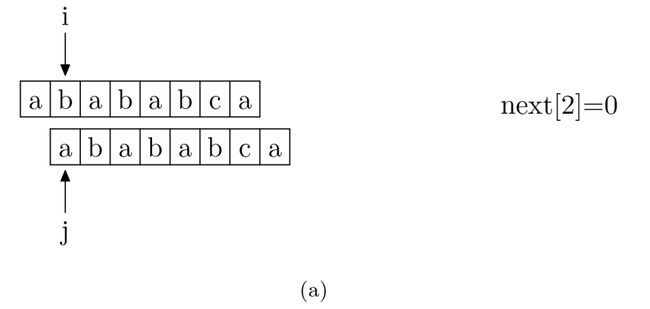
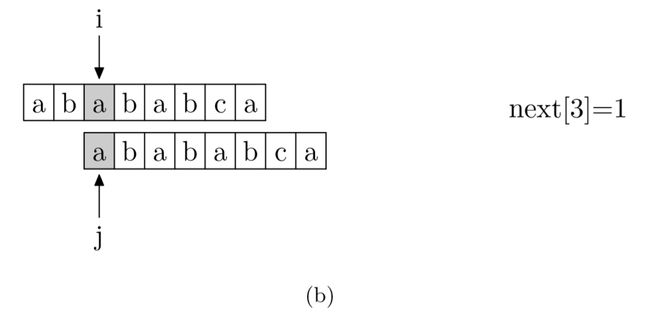
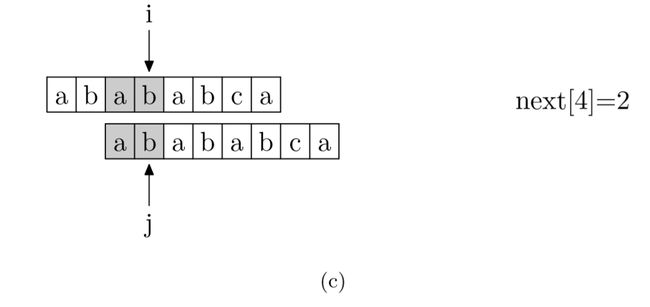
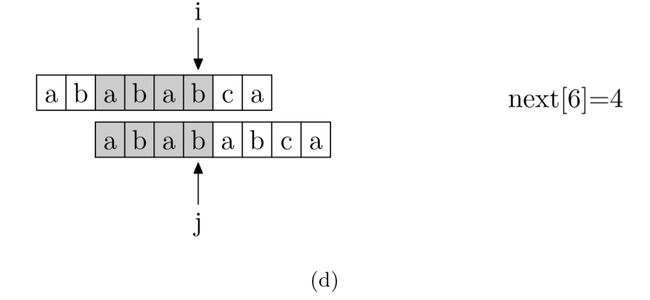
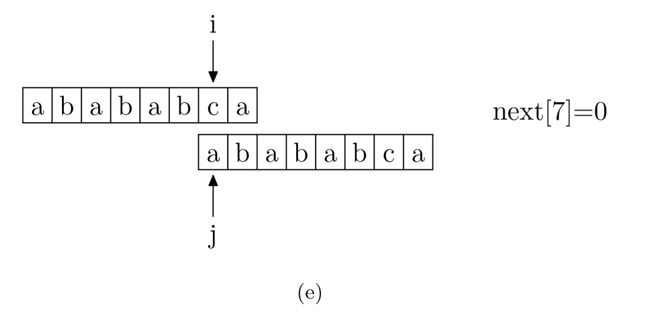
再来看一下如何快速求得 next 数组。其实，求 next 数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的 next 值就是匹配成功的字符串的长度

具体来说，就是从模式字符串的第一位（注意，不包括第 0 位）开始对自身进行匹配运算。 在任一位置，能匹配的最长长度就是当前位置的 next 值，如下图所示

代码如下：

void getNext(char *p, int *next) {
    next[0] = -1;
    int i = 0, j = -1;

    while (i < (int)strlen(p)) {
        if (j == -1 || p[i] == p[j]) {
            ++i;
            ++j;
            next[i] = j;
        } else {
            j = next[j];
        }
    }
}