【HBZ分享】java的大顶堆与小顶堆
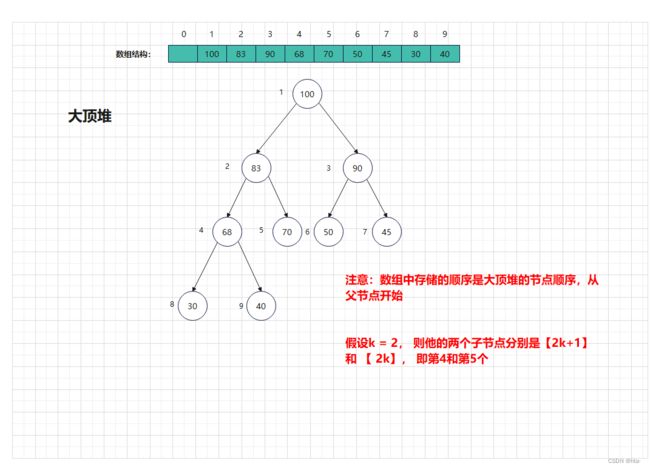
大顶堆
- 大顶堆属于完全二叉树的一种
- 大顶堆是父节点一定 大于 子节点
- 左右两个子节点没有顺序要求,左字节点大也行,有子节点大也可以
- 二叉堆就是我们所说的大顶堆 或 小顶堆
小顶堆
- 小顶堆也是完全二叉树
- 小顶堆是父节点一定 小于 子节点
- 左右两个子节点没有顺序要求,左字节点大也行,有子节点大也可以
- 二叉堆就是我们所说的大顶堆 或 小顶堆
存储原理 及 一些规则
- 一般做升序使用【大顶堆】, 做降序使用【小顶堆】,没错,你没看错,就是这样
- 堆是一个非线性结构,使用数组来存储完全二叉树非常省空间,可以把堆看作个数组
- 一般数组下标为【0】不存储数据,从【1】开始存储,这是为了方便使用
- 堆其实就是利用完全二叉树结构来维护数组
- 数组中下标为K的节点
(1). 左子节点下标为【2k】的节点
(2). 右子节点就是下标为【2k+1】的节点
(3). 父节点就是下标为【k/2】取整的节点, 当想把节点向上移动一层,只需要将当前节点的【下标/2】即可,想向下移动一层,就把当前节点【下标*2】 或 【下标 * 2 + 1】 - 注意:数组中存储的数据不是按照大小顺序存的,而是根据大顶堆 或 小顶堆的结构,从父到子, 从左到右一次存储的,所以数组本身是无序的, 如图:
- 公式描述:
大顶堆: arr[k] >= arr[2k + 1] && arr[k] >= arr[2k]
小顶堆: arr[k] <= arr[2k + 1] && arr[k] <= arr[2k]
使用场景
- 优先级队列:比如MQ产品
- 高精度定时器:比如定时任务
- TopK问题:海量数据中取得最大值,最小值场景
堆中元素的上下移动 与 插入
-
当想把节点向上移动一层,只需要将当前节点的【下标/2】即可,想向下移动一层,就把当前节点【下标*2】 或 【下标 * 2 + 1】
-
插入:比如插入个101, 则开始101会放在最后,然后用101和他的父节点进行比较,如果不符合大顶堆规则,则就和父节点交换位置,然后继续和父节点对比, 大顶堆规则就是父节点一定要比子节点大,即找到一个父节点大于插入的节点即可,如图所示:
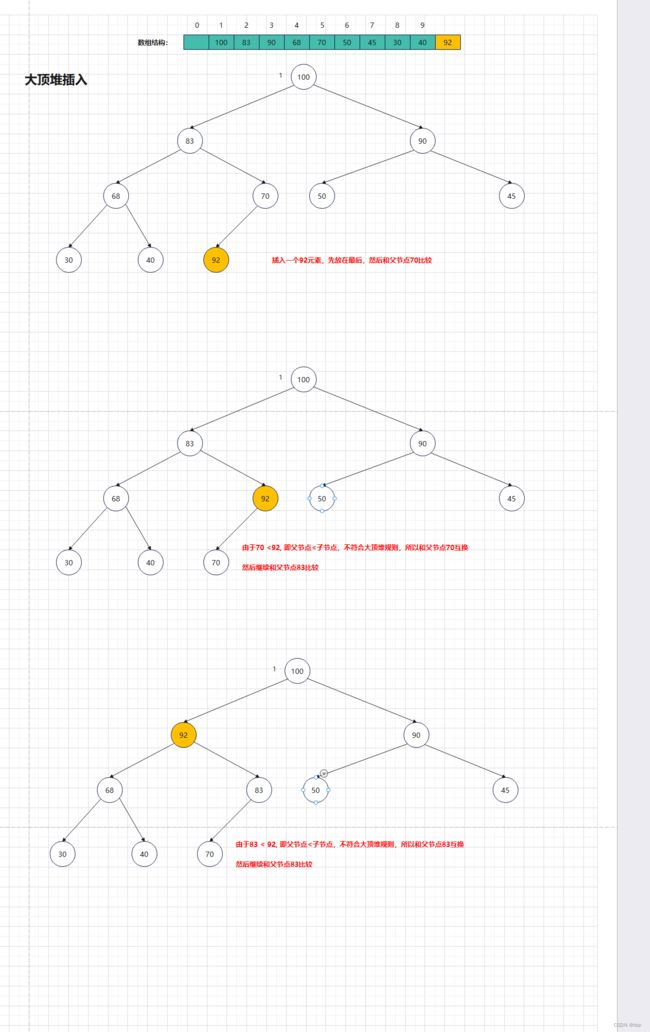
大顶堆代码实现
package 大顶堆;
public class Heap {
/**
* 存储元素的数组
*/
private int[] items;
/**
* 记录堆中元素个数
*/
private int num;
/**
* 构造方法,初始化数组容量
* @param capacity
*/
public Heap(int capacity){
// 因为第0位元素不存数据,所以容量要+1
this.items = new int[capacity + 1];
this.num = 0;
}
/**
* 向堆中插入数据
* @param value
*/
public void insert(int value){
// 新增元素默认会加到数组最后面
// ++num因为第一个元素不存储数据,所以存的位置要往后移动一位,就要先加1
items[++num] = value;
// 进行上浮操作, 把下标传过去即可
up(num);
}
/**
* 比较父子节点大小大小, item[parent]的元素是否小于item[child]元素的大小
*/
public boolean childBig(int parent, int child){
// 如果父节点 < 子节点,则返回true,表示需要交换
return items[parent] < items[child];
}
/**
* 交换父子节点元素位置
* @param parent
* @param child
*/
public void swap(int parent, int child){
int temp = items[parent];
items[parent] = items[child];
items[child] = temp;
}
/**
* 元素上浮
*
* 不断比较节点,直到items[k] < arr[k/2] 即 当前插入值小于父节点为止
* 条件: 当前节点为k
* 左右子节点 = items[2*k], items[2*k+1]
* 父节点 = items[k/2] 即k/2取整
*
*
* @param k 数组的下标
*/
private void up(int k){
// 父节点下标是>1的都要比较,等于1就没必要比较了,因为已经是第一位了
while (k > 1){
// 比较当前节点和父节点大小, k/2是父节点下标, k是子节点下标
if(childBig(k/2, k)){
// 如果子节点 > 父节点,则交换位置
swap(k/2, k);
}else{
// 如果小于,则直接break即可,不需要在比较了,因为比父节点小,那一定也比爷爷节点小
break;
}
// 当前节点要往上一层,则节点下标要更改为父节点的,然后循环继续和爷爷节点比较
k = k / 2;
}
}
/**
* 元素下沉
*
* 步骤
* 先判断他是否有子节点,即判断2*k < num, 第一波k = 1, num是最大元素个数
* 如果存在2 * k的位置则表示存在子节点,此时再看看是否存在右节点,即2 * k + 1 < num
* 如果存在右节点,则比较左右节点,并选出大的那个来和k节点进行比较
* 如果子节点 大于 父节点k, 则需要将父节点 和 子节点交换位置,即下沉
* 如此反复比较,知道k没有子节点为止
* @param k
*/
private void down(int k){
// 存在子节点时再进行while循环
while (2 * k < num){
// 存储左右子节点大的那个值的【下标】
int maxValue;
// 判断是否存在右节点
if(2 * k + 1 < num){
// 比较左右节点大小,【假设左为父,右为子】
if(childBig(items[2 * k], items[2 * k + 1])){
// 右节点大
maxValue = 2 * k + 1;
}else{
// 左节点大
maxValue = 2 * k;
}
}else{
// 不存在右子节点,则左节点就是大的值
maxValue = 2 * k;
}
// 把当前k节点和较大的子节点比较
if(childBig(k, items[maxValue])){
// 子节点大则交换父子节点位置
swap(k, maxValue);
// 当前节点要下沉一层,则节点下标要更改为子节点的,然后循环继续和孙子节点比较
k = maxValue;
}else{
// 子节点小,则不用再比较了,孙子节点一定更小,直接中断循环
break;
}
}
}
/**
* 删除堆中最大元素
*
* 流程:
* 删除下标为1的最大节点,然后把最后一个节点放到下标为1的位置,即最小的先放到最大的位置
* 将最后一个节点位置值设置为0 或 空,然后元素个数01
* 用下标为1的新值去和他的两个子节点比较
* 先判断他是否有子节点,即判断2*k < num, 第一波k = 1, num是最大元素个数
* 如果存在2 * k的位置则表示存在子节点,此时再看看是否存在右节点,即2 * k + 1 < num
* 如果存在右节点,则比较左右节点,并选出大的那个来和k节点进行比较
* 如果子节点 大于 父节点k, 则需要将父节点 和 子节点交换位置,即下沉
* 如此反复比较,知道k没有子节点为止
*
* @return
*/
public int delMax(){
// 删除下标为1的最大节点,然后把最后一个节点放到下标为1的位置,即最小的先放到最大的位置
int maxValue = items[1];
// 将最后一个节点和第一个节点交换,即把最后一个节点放到下标为1的位置
swap(1, num);
// 将最后一个节点设置为0,并将元素总个数-1
items[num] = 0;
num--;
// 通过下沉,重新堆化, 节点k = 1, 所以传1
down(1);
return maxValue;
}
}
大顶堆实战 之 优先级队列,通过权重weight来判断优先
MaxHeapPriorityQuere:
package 大顶堆;
/**
* 大顶堆实战之优先级队列
* >是应为要用compareTo比较大小,所以需要加上
*/
public class MaxHeapPriorityQueue > {
/**
* 存储队列元素
*/
private T[] items;
/**
* 记录队列元素个数
*/
private int num;
public MaxHeapPriorityQueue(int capacity){
// 数组下标为0,不存储数据,所以总长度要+1
this.items = (T[])new Comparable[capacity + 1];
// 开始队列元素肯定是0
this.num = 0;
}
/**
* 判断队列元素是否为空,为空就不消费了
*/
public boolean isEmpty(){
return num == 0;
}
/**
* 比较父子节点大小大小, item[parent]的元素是否小于item[child]元素的大小
*
* items[parent] = 案例中Task类型的对象,用Task对象.compareTo, 也就是在Task类中,必须有compareTo方法
* 所以Task类里面需要实现Comparable, 并写比较逻辑
*/
public boolean childBig(int parent, int child){
// 如果父节点 < 子节点,则返回true,表示需要交换
// T泛型比较用compareTo
return items[parent].compareTo(items[child]) < 0;
}
/**
* 向堆中插入数据
* @param value
*/
public void insert(T value){
// 新增元素默认会加到数组最后面
// ++num因为第一个元素不存储数据,所以存的位置要往后移动一位,就要先加1
items[++num] = value;
// 进行上浮操作, 把下标传过去即可
up(num);
}
/**
* 交换父子节点元素位置
* @param parent
* @param child
*/
public void swap(int parent, int child){
T temp = items[parent];
items[parent] = items[child];
items[child] = temp;
}
/**
* 元素上浮
*
* 不断比较节点,直到items[k] < arr[k/2] 即 当前插入值小于父节点为止
* 条件: 当前节点为k
* 左右子节点 = items[2*k], items[2*k+1]
* 父节点 = items[k/2] 即k/2取整
*
*
* @param k 数组的下标
*/
private void up(int k){
// 父节点下标是>1的都要比较,等于1就没必要比较了,因为已经是第一位了
while (k > 1){
// 比较当前节点和父节点大小, k/2是父节点下标, k是子节点下标
if(childBig(k/2, k)){
// 如果子节点 > 父节点,则交换位置
swap(k/2, k);
}else{
// 如果小于,则直接break即可,不需要在比较了,因为比父节点小,那一定也比爷爷节点小
break;
}
// 当前节点要往上一层,则节点下标要更改为父节点的,然后循环继续和爷爷节点比较
k = k / 2;
}
}
/**
* 元素下沉
*
* 步骤
* 先判断他是否有子节点,即判断2*k < num, 第一波k = 1, num是最大元素个数
* 如果存在2 * k的位置则表示存在子节点,此时再看看是否存在右节点,即2 * k + 1 < num
* 如果存在右节点,则比较左右节点,并选出大的那个来和k节点进行比较
* 如果子节点 大于 父节点k, 则需要将父节点 和 子节点交换位置,即下沉
* 如此反复比较,知道k没有子节点为止
* @param k
*/
private void down(int k){
// 存在子节点时再进行while循环
while (2 * k < num){
// 存储左右子节点大的那个值的【下标】
int maxValue;
// 判断是否存在右节点
if(2 * k + 1 < num){
// 比较左右节点大小,【假设左为父,右为子】
if(childBig(2 * k, 2 * k + 1)){
// 右节点大
maxValue = 2 * k + 1;
}else{
// 左节点大
maxValue = 2 * k;
}
}else{
// 不存在右子节点,则左节点就是大的值
maxValue = 2 * k;
}
// 把当前k节点和较大的子节点比较
if(childBig(k, maxValue)){
// 子节点大则交换父子节点位置
swap(k, maxValue);
// 当前节点要下沉一层,则节点下标要更改为子节点的,然后循环继续和孙子节点比较
k = maxValue;
}else{
// 子节点小,则不用再比较了,孙子节点一定更小,直接中断循环
break;
}
}
}
/**
* 删除堆中最大元素
*
* 流程:
* 删除下标为1的最大节点,然后把最后一个节点放到下标为1的位置,即最小的先放到最大的位置
* 将最后一个节点位置值设置为0 或 空,然后元素个数01
* 用下标为1的新值去和他的两个子节点比较
* 先判断他是否有子节点,即判断2*k < num, 第一波k = 1, num是最大元素个数
* 如果存在2 * k的位置则表示存在子节点,此时再看看是否存在右节点,即2 * k + 1 < num
* 如果存在右节点,则比较左右节点,并选出大的那个来和k节点进行比较
* 如果子节点 大于 父节点k, 则需要将父节点 和 子节点交换位置,即下沉
* 如此反复比较,知道k没有子节点为止
*
* poll 也叫弹出队列元素,其实就是删除
*
* @return
*/
public T poll(){
// 删除下标为1的最大节点,然后把最后一个节点放到下标为1的位置,即最小的先放到最大的位置
T maxValue = items[1];
// 将最后一个节点和第一个节点交换,即把最后一个节点放到下标为1的位置
swap(1, num);
// 将最后一个节点设置为0,并将元素总个数-1
items[num] = null;
num--;
// 通过下沉,重新堆化, 节点k = 1, 所以传1
down(1);
return maxValue;
}
public static void main(String[] args) {
MaxHeapPriorityQueue queue = new MaxHeapPriorityQueue<>(20);
queue.insert(new Task("任务100", 100));
queue.insert(new Task("任务20", 20));
queue.insert(new Task("任务198", 198));
queue.insert(new Task("任务24", 24));
queue.insert(new Task("任务66", 66));
while (!queue.isEmpty()){
Task poll = queue.poll();
poll.doTask();
}
}
}
Task执行任务的类:
package 大顶堆;
/**
* 任务对象,该对象会存储到Heap堆中
*/
public class Task implements Comparable{
/**
* 权重优先级,数字越大,优先级越高
*/
private int weight;
/**
* 任务名称
*/
private String name;
public Task(String name, int weight){
this.name = name;
this.weight = weight;
}
/**
* 执行task
*/
public void doTask(){
System.out.println(name + "task运行, 权重 =" + weight);
}
/**
* 重写Comparable,就是写比较逻辑,给Heap中的comparable用
* @param task the object to be compared.
* @return
*/
@Override
public int compareTo(Task task) {
// 调用者里面的weight和要比较的参数weight作比较
// this.weight是调用compareTo中的weight
// task.weight是传入参数的weight,即被比较者的
return this.weight - task.weight;
}
}