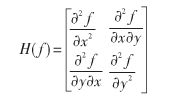特征点提取—尺度不变特征SIFT算法

目录

SIFT算法概述 

尺度空间与与金字塔表达

1 高斯模糊

2 金字塔构建

2.1 金字塔多分辨率

3、空间极值点检测(关键点的初步探查)

4、关键点描述

4.1 KPD生成

4.2、关键点的主方向（具有了旋转不变形）

5、关键点匹配

---

SIFT算法概述 

       尺度不变特征变换(Scale-invariant feature transform， 简称SIFT)是图像局部特征提取的现代方法——基于区域/图像块的分析。在上篇笔记里我们使用的图像之间对应点的匹配方法，不适用于不同尺度的图像。有许多应用场景需要对不同尺度（即分辨率、缩放、旋转角度、亮度等都可能存在不同）的图像进行特征识别和匹配，这就需要一种特征提取方法，通过这种方法提取出来的特征描述，可以不受尺度的影响，SIFT算法就是这种方法的实现。SHIT算法有如下的特点：SIFT特征是图像的局部特征，其对旋转、尺度缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定程度的稳定性。

     SIFT 特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、些微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取。SIFT算法在一定程度上可解决：

1. 目标的旋转、缩放、平移（RST）

2. 图像仿射/投影变换（视点viewpoint）

3. 光照影响（illumination）

      SIFT算法的实质是在不同的尺度空间上查找关键点(特征点)，并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等。 

Lowe将SIFT算法分解为如下四步：

1. 尺度空间极值检测：搜索所有尺度上的图像位置。通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点。

2. 关键点定位：在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。

3. 方向确定：基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换，从而提供对于这些变换的不变性。

4. 关键点描述：在每个关键点周围的邻域内，在选定的尺度上测量图像局部的梯度。这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变化。

尺度空间与与金字塔表达

       尺度空间使用高斯金字塔表示。Tony Lindeberg指出尺度规范化的LoG(Laplacion of Gaussian)算子具有真正的尺度不变性，Lowe使用高斯差分金字塔近似LoG算子，在尺度空间检测稳定的关键点。

      尺度空间理论的基本思想是：在图像信息处理模型中引入一个被视为尺度的参数，通过连续变化尺度参数获得多尺度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作为一种特征向量，实现边缘、角点检测和不同分辨率上的特征提取等。尺度空间方法将传统的单尺度图像信息处理技术纳入尺度不断变化的动态分析框架中，更容易获取图像的本质特征。尺度空间中各尺度图像的模糊程度逐渐变大，能够模拟人在距离目标由近到远时目标在视网膜上的形成过程。尺度越大图像越模糊。

      用机器视觉系统分析未知场景时，计算机并不预先知道图像中物体的尺度。我们需要同时考虑图像在多尺度下的描述，获知感兴趣物体的最佳尺度。另外如果不同的尺度下都有同样的关键点，那么在不同的尺度的输入图像下就都可以检测出来关键点匹配，也就是尺度不变性。图像的尺度空间表达就是图像在所有尺度下的描述。

     尺度空间满足视觉不变性。该不变性的视觉解释如下：当我们用眼睛观察物体时，一方面当物体所处背景的光照条件变化时，视网膜感知图像的亮度水平和对比度是不同的，因此要求尺度空间算子对图像的分析不受图像的灰度水平和对比度变化的影响，即满足灰度不变性和对比度不变性。另一方面，相对于某一固定坐标系，当观察者和物体之间的相对位置变化时，视网膜所感知的图像的位置、大小、角度和形状是不同的，因此要求尺度空间算子对图像的分析和图像的位置、大小、角度以及仿射变换无关，即满足平移不变性、尺度不变性、欧几里德不变性以及仿射不变性。

1 高斯模糊

     高斯核是唯一可以产生多尺度空间的核（《Scale-space theory: A basic tool for analysing structures at different scales》）。一个图像的尺度空间L(x,y,σ) ,定义为原始图像I(x,y)与一个可变尺度（就是高斯函数中sigma值(σ)不一样）的2维高斯函数G(x,y,σ)卷积运算。尺度空间因子的值越小表示图像被平滑的越少，相应的尺度也就越小。大尺度对应于图像的概貌特征，小尺度对应于图像的细节特征。

          二维空间高斯函数：

                                                      

      尺度空间：

                                                      

尺度是自然客观存在的，不是主观创造的。高斯卷积只是表现尺度空间的一种形式。

二维空间高斯函数是等高线从中心成正太分布的同心圆：

                                                      

分布不为零的点组成卷积阵与原始图像做变换，即每个像素值是周围相邻像素值的高斯平均。一个5*5的高斯模版如下所示：

                                                    

        高斯模版是圆对称的，且卷积的结果使原始像素值（中心值）有最大的权重，距离中心越远的相邻像素值权重也越小。在实际应用中，在计算高斯函数的离散近似时，在大概3σ距离之外的像素都可以看作不起作用，这些像素的计算也就可以忽略。所以，通常程序只计算(6σ+1)*(6σ+1)就可以保证相关像素影响。

     高斯模糊另一个很厉害的性质就是线性可分：使用二维矩阵变换的高斯模糊可以通过在水平和竖直方向各进行一维高斯矩阵变换相加得到。O(N^2*m*n)次乘法就缩减成了O(N*m*n)+O(N*m*n)次乘法。（N为高斯核大小，m,n为二维图像高和宽）

            

2 金字塔构建

2.1 金字塔多分辨率

        金字塔是早期图像多尺度的表示形式。图像金字塔化一般包括两个步骤：使用低通滤波器平滑图像；对平滑图像进行降采样（通常是水平，竖直方向1/2），从而得到一系列尺寸缩小的图像。而对于二维图像，一个传统的金字塔中，每一层图像由上一层分辨率的长、宽各一半，也就是四分之一的像素组成：

                                                                 

        如上图所示，图像的金字塔模型是指，将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，从下到上构成的塔状模型。原图像为金子塔的第一层，每次降采样所得到的新图像为金字塔的一层(每层一张图像，此时还没有对金字塔每层图像用不同参数的σ做高斯模糊)，每个金字塔共n层。金字塔的层数根据图像的原始大小和塔顶图像的大小共同决定：如对于大小为512*512的图像，金字塔上各层图像的大小如表3.1所示，当塔顶图像为4*4时，n=7，当塔顶图像为2*2时，n=8。

多尺度和多分辨率

尺度空间表达和金字塔多分辨率表达之间最大的不同是：

尺度空间表达是由不同高斯核平滑卷积得到，在所有尺度上有相同的分辨率(图像的大小不会发生变化，假设原图像是640*320，不同尺度表达后的图像大小依然是640*320，只是模糊成都不同)；

而金字塔多分辨率表达每层分辨率减少固定比率（图像大小在变，原图像是640*320，变成320*160，再变成160*80......）。

       所以，金字塔多分辨率生成较快，且占用存储空间少（单纯降采样）；而多尺度表达随着尺度参数的增加冗余信息也变多（多次卷积）。多尺度表达的优点在于图像的局部特征可以用简单的形式在不同尺度上描述；而金字塔表达没有理论基础，难以分析图像局部特征。

 2.2  高斯差分DoG金字塔

   DOG（Difference of Guassian）：简称  高斯函数的差分，是灰度图像增强和角点检测的一种方法。将目标图像与高斯函数进行卷积运算得到一幅目标图像的低通滤波结果，此过程称为去燥。

                                           

  在某一尺度上的特征检测可以通过两个相邻高斯尺度空间的图像相减，得到DOG的响应值图像。详细过程如下：

         首先 ：对一幅图像f（x，y）进行不同参数的高斯滤波计算，表示如下

         其次：将滤波得到的结果g1（x,y）和g2（x,y）相减得到：

         

即：可以将DOG表示为：

             

注：在具体的图像处理中，就是将两幅不同参数下的高斯滤波结果相减。得到DOG图。

 

 上图为一个高斯平滑参数为0.3，另一个高斯平滑参数为0.4得到的DOG图像

---

      结合尺度空间表达和金字塔多分辨率表达，就是在使用尺度空间时使用金字塔表示，也就是计算机视觉中最有名的拉普拉斯金子塔。高斯拉普拉斯LoG（Laplace of Guassian）算子就是对高斯函数进行拉普拉斯变换：

                                         

     但我们一般采用DoG算子。DoG（Difference of Gaussian）其实是对高斯拉普拉斯LoG的近似。SIFT算法建议，在某一尺度上的特征检测可以通过对两个相邻高斯尺度空间的图像相减，得到DoG的响应值图像D(x,y,σ)。然后仿照LoG方法，通过对响应值图像D(x,y,σ)进行局部最大值搜索，在空间位置和尺度空间定位局部特征点。其中  k为相邻两个尺度空间倍数的常数：

                            

        

     上图中（a）是DoG的三维图，（b）是DoG与LoG的对比。为了得到DoG图像，先要构造高斯金字塔。我们回过头来继续说高斯金字塔~

        高斯金字塔在多分辨率金字塔简单降采样基础上加了高斯滤波，也就是对金字塔每层图像用不同参数的σ做高斯模糊，使得每层金字塔有多张高斯模糊图像。金字塔每层多张图像合称为一组（Octave），每组有多张（也叫层Interval）图像。另外，降采样时，金字塔上边一组图像的第一张图像（最底层的一张）是由前一组（金字塔下面一组）图像的倒数第三张隔点采样得到。

                                         

 

     上面这句话——“对金字塔每层图像用不同参数的σ做高斯模糊，使得每层金字塔有多张高斯模糊图像”的意思就是：先对降采样后的每张图像使用不同的sigma进行高斯模糊，结果是每个降采样图像对应一组模糊图像：

                  

然后对每组模糊图像的相邻图像作DOG，结果是每个降采样图像对应一组DOG图像，如图：

                                     

把每一组图像堆叠起来，位于塔底的是第一组（first octave），往上是第二组，第三组...每一组的图像大小为前一组的一半，看起来像金字塔：

                      

构建高斯金字塔之后，就是用金字塔相邻图像相减构造DoG金字塔，最终结果就是如下图所示：

                                    

 

3、空间极值点检测(关键点的初步探查)

3.1 极值点检测

      关键点是由DOG空间的局部极值点组成的，DOG值对噪声和边缘比较敏感，需要去除不稳定和错误检测出的极值点，关键点的初步探查是通过同一Octave内各DoG相邻两层图像之间比较完成的。为了寻找DoG函数的极值点，每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。如下图所示，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点（就是每组（Octave）内不同Interval，因为前面对每组（Octave）不同层Interval进行了不同的sigma进行了高斯模糊所以就是不同的尺度）比较，以确保在尺度空间和二维图像空间都检测到极值点。 

    如上图所示，每组（Octave）含4层的高斯差分金子塔，只能在中间两层中进行两个尺度的极值点检测，其它尺度则只能在不同组中进行。为了在每组中检测S个尺度的极值点，则DOG金字塔每组需S+2层图像，而DOG金字塔由高斯金字塔每组中相邻两层相减得到，则高斯金字塔每组需S+3层图像，实际计算时S在3到5之间。

      SIFT分别对每组DOG图像提取关键点，以第一组为例，将第一组DOG图像上下对齐叠加在一起，形成DOG空间，DOG空间有两个域：图像域和尺度域。图像域指图像本身的二维平面像素，尺度域指垂直于图像域的第三维度构成的像素。SIFT使用局部极值检测来定位找到关键点，如下图所示：

                                                   

3.2 关键点的定位

     以上极值点的搜索是在离散空间进行搜索的，由下图可以看到，在离散空间找到的极值点不一定是真正意义上的极值点。可以通过对尺度空间DoG函数进行曲线拟合寻找极值点来减小这种误差。

                                                  

    插值需要将离散的图像表达式，表达为连续的函数。以下通过拟合三维二次函数（二阶的泰勒展开式）来精确确定关键点的位置和尺度。对尺度空间方程D(x,y,σ)使用了泰勒级数展开（到二阶）变换，把样本点作为原点。利用DoG函数在尺度空间的Taylor展开式： 
                                                

关键点的精确位置就在上式极值点所在位置，对上述式子求导数并令导数为0，则极值点为：

 是位置和尺度三个变量的向量。其中D和它的导数是样本点的估值，而为这一点的补偿（偏移量）。通过对函数求关于x的偏导并设为零得到极值的位置 ：

                                                         

from :https://blog.csdn.net/hujingshuang/article/details/44995829

其中f是某一尺度为δ的DoG层,二维函数，其泰勒展开式为：

                    
写成向量形式：

                    

关键点的精确位置就在上式极值点所在位置，对上述式子求导数并令导数为0，则有：

                                         

其中f是某一尺度为δ的DoG层。Z=【△x、△y】，即所求极值点相对于关键点的偏移量，若任意一个偏移量超过了0.5，则说明拟合关键点应该在原关键点的相邻位置。在该DoG层不断迭代拟合，确定新关键点位置，直至偏移量都小于0.5（即稳定的关键点）为止。

下一步去除低响应值的点，再删除边缘效应。

3.3 消除边缘响应

    一个定义不好的高斯差分算子的极值在横跨边缘的地方有较大的主曲率，而在垂直边缘的方向有较小的主曲率。DOG算子会产生较强的边缘响应，需要剔除不稳定的边缘响应点。获取特征点处的Hessian矩阵，主曲率通过一个2x2 的Hessian矩阵H求出：

                                                         

     Hessian方阵实际上就是二维变量的二阶导数，用来表示各个方向上的梯度变化。其几何意义就是，其两个特征值越大，该点所在局部区域凸性越强，变化就越大。而边缘点则是一个特征值很小，而另一个特征值较大。

     H的特征值α和β代表x和y方向的梯度，假设是α较大的特征值，而是β较小的特征值，则较大特征值所对应的特征向量是垂直于直线的，较小特征值对应的特征向量是沿着直线方向的，两个特征值的比值越大，即在某一个方向的梯度值越大，而在另一个方向的梯度值越小，而边缘恰恰就是这种情况。所以为了剔除边缘响应点，需要让该比值小于一定的阈值，因此，只要检测两个特征值的比率，大于阈值，即为边缘。

4、关键点描述

       SIFT的提取的特征（关键点）需要保持尺度不变性，所以这里讲的关键点，比角点和兴趣点稍为复杂些，SIFT关键点需要携带尺度信息，包括缩放、方向等信息，主要由它周围的像素来贡献。如果用一个向量来存储这些信息，此向量称为关键点描述（key point descriptor，简称KPD）。

4.1、关键点的主方向（具有了旋转不变形）

       生成关键点的KPD之前，要先求出该关键点的主方向。为了让关键点对方向具有不变性，在选取16x16矩形区域的时候，将矩形的方向旋转到与关键点主方向一致。为了使描述符具有旋转不变性，需要利用图像的局部特征为给每一个关键点分配一个基准方向。使用图像梯度的方法求取局部结构的稳定方向。

       SIFT定义关键点主方向为：以关键点为中心的周围像素所贡献的主方向。可采用梯度直方图统计法，统计以关键点为原点，一定区域内的图像像素点对关键点方向生成所作的贡献，贡献最大的那个方向即为关键点主方向。具体方法如下：

       1、对于在DOG金字塔中检测出的关键点，采集其所在高斯金字塔图像3σ邻域窗口内像素的梯度和方向分布特征。

       2、在完成关键点的梯度计算后，使用直方图统计邻域内像素的梯度和方向。梯度直方图将0~360度的方向范围分为36个柱(bins)。如下图所示，直方图的峰值方向代表了关键点的主方向，(为简化，图中只画了八个方向的直方图)。

                         

                           

      3、 方向直方图的峰值则代表了该特征点处邻域梯度的方向，以直方图中最大值作为该关键点的主方向。这样在求解该关键点描述符时，取得16*16的矩形框以主方向为准

      为了增强匹配的鲁棒性，保留峰值大于主方向峰值80％的方向作为该关键点的辅方向。因此，对于同一梯度值的多个峰值的关键点位置，在相同位置和尺度将会有多个关键点被创建但方向不同。仅有15％的关键点被赋予多个方向，但可以明显的提高关键点匹配的稳定性。实际编程实现中，就是把该关键点复制成多份关键点，并将方向值分别赋给这些复制后的关键点，并且，离散的梯度方向直方图要进行插值拟合处理，来求得更精确的方向角度值。至此，将检测出的含有位置、尺度和方向的关键点即是该图像的SIFT特征点。

     经过上述过程，我们特征点的所有量（x,y,σ,θ）都已经已经求得，其中位置（x,y）、尺度σ都是在上一节中求得，而特征点方向θ是通过特征点邻域直方图求得。接下来就是为每个关键点建立一个描述符，用一组向量将这个关键点描述出来，使其不随各种变化而改变，比如光照变化、视角变化等等。这个描述子不但包括关键点，也包含关键点周围对其有贡献的像素点，并且描述符应该有较高的独特性，以便于提高特征点正确匹配的概率。

4.2、 KPD生成

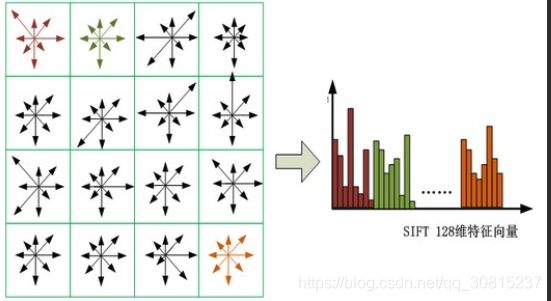
       SIFI 描述子h(x, y, θ)是对特征点附近邻域内高斯图像梯度统计结果的一种表示，它是一个三维的阵列，但通常将它表示成一个矢量。矢量是通过对三维阵列按一定规律进行排列得到的。特征描述子与特征点所在的尺度有关，因此，对梯度的求取应在特征点对应的高斯图像上进行。将特征点附近邻域划分成4 *4个子区域，每个子区域的尺寸为3σ个像元，σ为特征点的尺度值。考虑到实际计算时，需要采用双线性插值，计算的图像区域为3σ(4+ 1)。如果再考虑旋转的因素，那么，实际计算的图像区域应大于3σ(4+ 1)√2。

    为了保证特征矢量具有旋转不变性，需要以特征点为中心，将特征点附近邻域内(3σ(4+ 1)√2，3σ(4+ 1)√2)图像梯度的位置和方向旋转一个方向角θ，即将原图像x轴转到与主方向相同的方向。旋转公式如下。

                                                                        

 

　在特征点附近邻域图像梯度的位置和方向旋转后，再以特征点为中心，在旋转后的图像中取一个3σ4 x 3σ4大小的图像区域。并将它等间隔划分成4 X4个子区域，每个间隔为3σ像元。

     在每子区域内计算8个方向的梯度方向直方图，绘制每个梯度方向的累加值，形成一个种子点。与求特征点主方向时有所不同，此时，每个子区域的梯度方向直方图将0° ~360°划分为8个方向范围，每个范围为45°，这样，每个种子点共有8个方向的梯度强度信息。由于存在4X4个子区域，所以，共有4X4X8=128个数据，最终形成128维的SIFT特征矢量。同样，对于特征矢量需要进行高斯加权处理，加权采用方差为3σ*4/2的标准高斯函数，其中距离为各点相对于特征点的距离。使用高斯权重的是为了防止位置微小的变化给特征向量带来很大的改变，并且给远离特征点的点赋予较小的权重，以防止错误的匹配。 

                

               

     为了去除光照变化的影响，需对上述生成的特征向量进行归一化处理，在归一化处理后，对特征矢量大于0.2的要进行截断处理，即大于0.2的值只取0.2，然后重新进行一次归一化处理，其目的是为了提高鉴别性

from：https://www.cnblogs.com/JiePro/p/sift_4.html

 

KPD生成步骤：

1、在关键点所在图像上，划出以关键点为中心的16x16的矩形图像：

2、将16x16矩形图像划分为16小格，每小格为4x4，并计算每个像素的梯度和幅度（即像素值变化的方向及大小）：

  

3、对每个小格进行统计，统计8个方向的幅度，形成梯度直方图：

  

4、将16小格的幅度直方图连接起来，用向量表示，即为KPD，共有128（8x16）维，使用向量表示为： R = (r1, r2, ..., r128)：

  

5、去除光照变化的影响，需对上述生成的特征向量进行归一化处理。

5、关键点匹配

     关键点的匹配问题，已经转为KPD的匹配问题，两KPD的相似程度，使用欧式距离进行计算。设有两个KPD分别为R = (r1, r2, ..., r128)和S = (s1, s2, ..., s128)，R与S的欧式距离计算公式为：

d = sqrt((r1 - s1)^2 + (r2 - s2)^2 + ... + (r128 - s128)^2)

要找出两张不同尺度图像间的对应点（具有对应关系的关键点），分下面几步：

1、分别检测两张图像的关键点，并计算出每个关键点的KPD，分别得到两个KPD集合SET1和SET2;

2、为SET1中每个KPD，从SET2找最佳匹配（即欧式距离最小的为最佳匹配），然后反过来，为SET2每个KPD，从SET1中找最佳匹配，只有彼此认为是最佳匹配的那些KPD对才是对应点;

     为提高匹配准确率，可以设定一个阈值，欧式距离大于此阈值的那些匹配对，将不考虑。为提高算法效率，可以使用kd树和RANSAC（ Random Sample Consensus， 随机抽样一致）方法。

1. 在我们的匹配点中随机选择4对点。这四对叫做局内点或者内点，而其他的匹配点叫做局外点或者外点
2. 根据4对内点得到内部的单应性矩阵
3. 单应性矩阵测试所有其他外点，通过一个阈值将所有的外点分为两部分：所有满足这个单应性的外点被归为是新的内点；而所有不满足的外点被归为新的外点
4. 获取我们所有的内点（新的内点+旧的内点）并转到步骤2
5. 只要没有更改或我们已经迭代步骤2-步骤4 k次，结束迭代。最终的单应矩阵将是我们想要的。
    

from：https://blog.csdn.net/samkieth/article/details/50407655

from:https://segmentfault.com/a/1190000004149225

from：https://blog.csdn.net/lyl771857509/article/details/79675137

实例请参考：https://mp.csdn.net/postedit/87261771