【数据库】函数依赖

1. 不良的模式设计

会造成各种异常现象，简单归为：

• 数据冗余
• 插入异常（有的信息无法插入）
• 删除异常（删除一部分却变成要删整条记录）
• 更新异常（容易漏改一部分记录造成数据不一致性）

不良特性分析：

• 插入异常：如果学生没有选课，关于他的个人信息及所在系的信息就无法插入
• 删除异常：如果删除学生的选课信息，则有关他的个人信息及所在系的信息也随之删除了
• 更新异常：如果学生转系，若他选修了k门课，则需要修改k次
• 数据冗余：如果一个学生选修了k门课，则有关他的所在系的信息重复

但冗余在一定程度上也可减小时间开销

这些异常，归根结底由数据依赖引起。其中,函数依赖是最重要的数据依赖

2. 函数依赖

2.1 关系模式的表示

关系模式的完整表示是一个五元组：
R〈U，D，Dom，F〉
其中：

• R为关系名；
• U为关系的属性集合；
• D为属性集U中属性的数据域；
• Dom为属性到域的映射；
• F为属性集U的数据依赖集。
  关系模式可以用三元组简单表示为：
  R〈U，F〉

2.2 函数依赖理论

• 关系模式中的各属性之间相互依赖、相互制约的联系称为数据依赖。
• 数据依赖一般分为函数依赖、多值依赖和连接依赖
• 其中,函数依赖是最重要的数据依赖

函数依赖（Functional Dependency）是关系模式中属性之间的一种逻辑依赖关系。

示例：

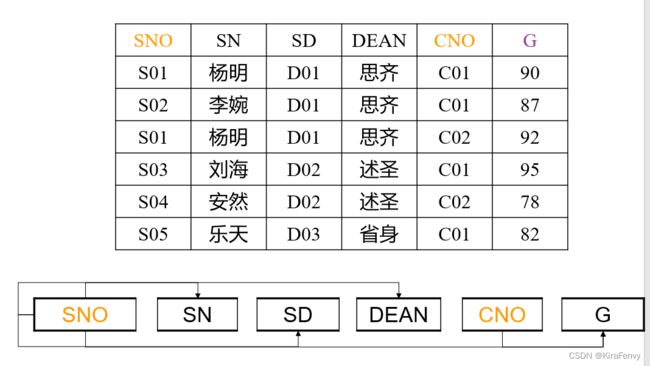
• 例如在上一节介绍的关系模式SCD中，SNO与SN、AGE、DEPT之间都有一种依赖关系。
• 由于一个SNO只对应一个学生，而一个学生只能属于一个学院，所以当SNO的值确定之后，SN，AGE，DEPT的值也随之被唯一的确定了。
• 这类似于变量之间的单值函数关系。设单值函数Y=F(X)，自变量X的值可以决定一个唯一的函数值Y。
• 在这里，我们说SNO决定函数（SN，AGE，DEPT），或者说（SN，AGE，DEPT）函数依赖于SNO。

2.2.1 函数依赖的定义

• 设关系模式R(U,F)，U是属性全集，F是U上的函数依赖集，X和Y是U的子集：
• 如果对于R(U)的任意一个可能的关系r，对于X的每一个具体值，Y都有唯一的具体值与之对应（也就是对任意t1、t2属于r, 如果 t1[X]=t2[X] 有t1[Y]=t2[Y]），则称X决定函数Y，或Y函数依赖于X，记作X→Y。我们称X为决定因素，Y为依赖因素。
• 当Y不函数依赖于X时，记作:X Y（箭头加一反斜杠）。
• 当X→Y且Y→X时，则记作：X ↔ Y（双边箭头）。
• 这类似于变量之间的单值函数关系。设单值函数Y=F(X)，自变量X的值可以决定一个唯一的函数值Y。

示例：

• 对于关系模式SCD
• U={SNO,SN,AGE,DEPT,MN,CNO,SCORE}
• F={SNO→SN，SNO→AGE，SNO→DEPT，…}
• 一个SNO有多个SCORE的值与其对应，因此SCORE不能唯一地确定，即SCORE不能函数依赖于SNO，所以有：SNO  SCORE。
• 但是SCORE可以被（SNO，CNO） 唯一地确定。所以可表示为：（SNO，CNO）→SCORE

2.2.2 平凡（trivial）/非平凡的函数依赖

简单来说平凡的函数依赖的成立是“自然而然”的集合包含关系造成的

2.2.3 完全/部分函数依赖

Y部分依赖于X意思就是Y只依赖X的一部分（真子集），类似超码与候选码

只有当决定因素是组合属性时，讨论部分函数依赖才有意义，当决定因素是单属性时，只能是完全函数依赖。

2.2.4 传递函数依赖

2.2.5 关于函数依赖的说明

1. 函数依赖是语义范畴的概念. 它反映了一种语义完整性约束,只能根据语义来确定一个函数依赖：

• 例如，对于关系模式S，当学生不存在重名的情况下，可以得到：
  • SN→AGE
  • SN→DEPT
• 这种函数依赖关系，必须是在没有重名的学生条件下才成立的，否则就不存在函数依赖了。
• 所以函数依赖反映了一种语义完整性约束。

2. 函数依赖关系的存在与时间无关。

• 因为函数依赖是指关系中的所有元组应该满足的约束条件，而不是指关系中某个或某些元组所满足的约束条件。
• 当关系中的元组增加、删除或更新后都不能破坏这种函数依赖。
• 因此，必须根据语义来确定属性之间的函数依赖，而不能单凭某一时刻关系中的实际数据值来判断。
• 例如，对于关系模式S，假设没有给出无重名的学生这种语义规定，则即使当前关系中没有重名的记录，也只能存在函数依赖SNO→SN，而不能存在函数依赖SN→SNO，因为如果新增加一个重名的学生，函数依赖SN→SNO必然不成立。
• 所以函数依赖关系的存在与时间无关，而只与数据之间的语义规定有关。

3．函数依赖与属性之间的联系类型有关。(了解)

• (1)在一个关系模式中，如果属性X与Y有1:1联系时，则存在函数依赖X→Y，Y→X，即X ↔ Y。
  • 例如，当学生无重名时，SNO与SN。
• (2)如果属性X与Y有m :1的联系时，则只存在函数依赖X→Y。
  • 例如，SNO与AGE，DEPT之间均为m:1联系，所以有SNO→AGE，SNO→DEPT。
• (3)如果属性X与Y有m:n的联系时，则X与Y之间不存在任何函数依赖关系。
  • 例如，一个学生可以选修多门课程，一门课程又可以为多个学生选修，所以SNO与CNO之间不存在函数依赖关系。
• 由于函数依赖与属性之间的联系类型有关，所以在确定属性间的函数依赖关系时，可以从分析属性间的联系类型入手，便可确定属性间的函数依赖。

3. 函数依赖的运算

3.1 逻辑蕴涵

有时候要根据给定的函数依赖，判断另外一些函数依赖是否存在

3.2 Amstrong公理系统

用途：求给定关系模式的码/键（Key）；从一组函数依赖求得蕴含的函数依赖

分解规则（版本2）：由X→Y及 Z含于Y，有X→Z （A1， A3推出）

可以两个式子“相乘”，X乘Y为XY，X乘X依然是X，两边相同部分没有包含关系不能直接相消（如XY->XZ等价于XY->Z），条件可以有冗余（如A→C可以推出AB→C，但由于不等价，所以少用）

注意：由自反律所得到的函数依赖均是平凡的函数依赖，自反律的使用并不依赖于F

引理 X→A1 A2…Ak成立的充分必要条件是X→Ai成立（i=1，2，…，k）。

例题：

3.3 闭包

3.3.1 函数依赖集的闭包

由F计算F+的算法（证明F+=F）

repeat：
	对于 F+ 中的每个函数依赖关系 f    
		对 f 应用**自反**和**增广**规则
		将生成的函数依赖关系添加到 F +
	对于 F + 中的每对功能依赖关系 f1 和 f2     
		如果 f1 和 f2 可以使用**传递性**进行组合，将生成的函数依赖关系添加到 F +
直到 F+ 不再有任何变化

判断一个属性集合X是否为超码？
可以通过计算F+ ，找出所有左半部是X的函数依赖，并且合并这些函数依赖的右半部，看是否包含了R上所有的属性（根据已有函数依赖，将属性集作为条件，能否推出所有属性，可以的话该属性集为超码）。

例子：

3.3.2 属性集上的闭包

即把X集合当中的属性作为已知条件，能推出的所有属性的集合为$X_F^{+}$

区别于函数依赖的闭包：$X_F^{+}$包含的是属性，而$F^{+}$包含的是函数依赖

算法：最多|U-X|步

例子：可以用来判断X是否是超码或者是候选码

求候选码的步骤：
1、求闭包证明是超码
2、对超码的所有真子集，其实取最大真子集就可以，来一遍同样的过程才可以判断

3.4 无关属性(extraneous attribute)

下面是形式化定义，看例子即可，其实就是在函数依赖上可有可无的属性

无关属性检验

一样，看例子即可

为了检验结果含无关属性（只要检验某半边含多个属性的就可以），计算去除无关属性后的闭包是否包含结果

3.5 正则覆盖(canonical cover)

函数依赖集的等价性：函数依赖集F，G，若F+ = G+，则称F与G等价

F的正则覆盖$F_c$是与F等价的“最小”依赖集，Fc满足以下性质：

• $F_c$中的任何函数依赖都不含无关属性
• $F_c$中函数依赖的左半部都是唯一的（但是A→BC和AD→E的左半部是不同的）

正则覆盖计算算法：

repeat
	使用合并律把F中左半边相同的合并
	在所有函数依赖中检验无关属性（只要检验某半边含多个属性的就可以），并去除无关属性
	检查F中剩余函数依赖有没有因为传递律而产生的，有就去除
until F	不再变化

注意：在删除某些无关属性后，合并律可能会变得适用，因此必须重新应用

例子：