数据结构 --线性存储结构-数组、链表、栈、队列
学习目标:
理解数组、链表、栈、队列的实现原理,熟练线性存储结构的使用
学习内容:
1、 基本理解 2、 深入理解具体实现 3、 实际用例一、基本理解和使用
一般来说,常用的数据结构分为线性数据结构和非线性数据结构,线性数据结构又分为数组、链表、栈和队列,所谓线性结构是指结构中的元素存在一个一对一的关系,下面具体说明;
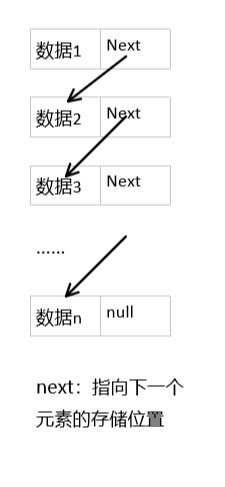
1、数组
数组是最基础的数据结构,是将相同类型的元素存储于连续的内存空间中;
数组由于其下标结构,查改效率很高,但非尾部增删效率差,而且也不适合存储特大量的数据。
如图

//创建一个整形数组
int[] nums;
//静态初始化
int[] nums = {1,2,3,4,5}
//动态初始化
int[] nums;
num[0] = 1;
num[1] = 2;
num[2] = 3;
num[3] = 4;
num[4] = 5;
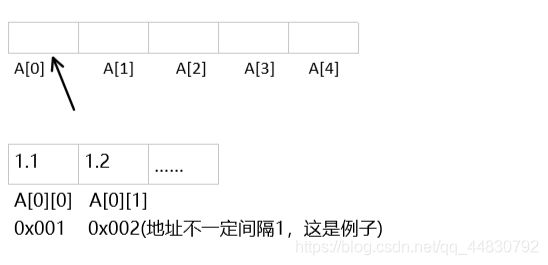
二维数组
二维数组是一种结构较为特殊的数组,只是将数组中的每个元素变成了一维数组。
类似一维数组,对于一个二维数组 A = [[1.1, 1.2, 1.3,1. 4],[2, 4, 5, 6],[1, 4, 6, 8]],计算机同样会在内存中申请一段 连续 的空间,并记录第一行数组的索引位置,即 A[0][0] 的内存地址,它的索引与内存地址的关系如下图所示。
可变长数组
上述数组在创建时需要设定长度,这个长度是无法改变的;基于数组,java中引入集合中的ArrayList实现可变长数组,即基于数组延申为一个集合类,
注意:集合和数组是有区别的,即ArrayList不是数组Array,可以使用Array =toArray(arraylistxxx)和ArrayList = asList(array)转化(因为泛型机制的存在,toArray()无参方法常出错,asList()方法也需要参数而不是直接调用)。
// 创建集合对象
ArrayList<String> list = new ArrayList<>();
// 添加元素
list.add("zhangsan");
list.add("lisi");
list.add("wangwu");
// 从集合中取出某个元素
// List集合有下标
String firstElt = list.get(0);
System.out.println(firstElt);
System.out.println("================");
// 遍历(下标方式)
for(int i = 0; i < list.size(); i++){
String elt = list.get(i);
System.out.println(elt);
}
System.out.println("================");
// 遍历(迭代器方式)
Iterator<String> it = list.iterator();
while(it.hasNext()){
System.out.println(it.next());
}
System.out.println("================");
// while循环修改为for循环
/*for(Iterator it2 = list.iterator(); it2.hasNext(); ){
System.out.println("====>" + it2.next());
}*/
// 遍历(foreach方式)
for(String s : list){
System.out.println(s);
}
System.out.println("================");
//lambda表达式
list.forEach(System.out::println);
2、链表
链表不同于数组,在内存地址上是不连续的,这使得它的增删效率高,但查改效率不如数组。一个链表节点一般包括值val和(指针)下一个节点引用信息指向直接后继。
单链表
循环链表
循环链表是特殊形式的单链表,它的最后一个节点的指针与指向头节点,整个链表形成一个环。从任一节点出发均可找到其他节点
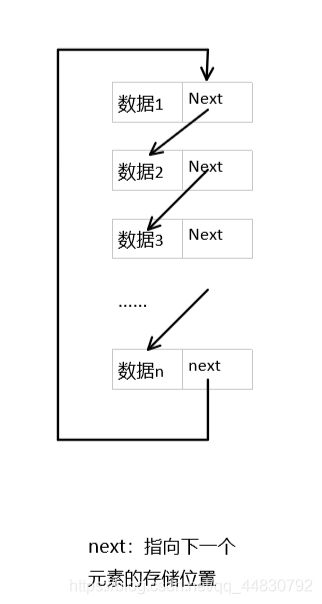
为了克服链表的单向性,又引入了双链表,即拥有两个指针域的链表,增加了一个指向直接前驱的指针域。
双向链表
//单链表的简单实现
class ListNode {
int val; // 节点值
ListNode next; // 后继节点引用
ListNode(int x) { val = x; }
}
// 实例化节点
ListNode n1 = new ListNode(4); // 节点 head
ListNode n2 = new ListNode(5);
ListNode n3 = new ListNode(1);
// 构建引用指向
n1.next = n2;
n2.next = n3;
//遍历方式
ListNode head=n1;
while(head!=null){
System.out.println(head.val);
head=head.next;
}
双向链表的使用
java中的集合LinkedList基层为双向链表。
LinkedList和ArrayList都是线性结构同实现了一个List接口大多方法通用。
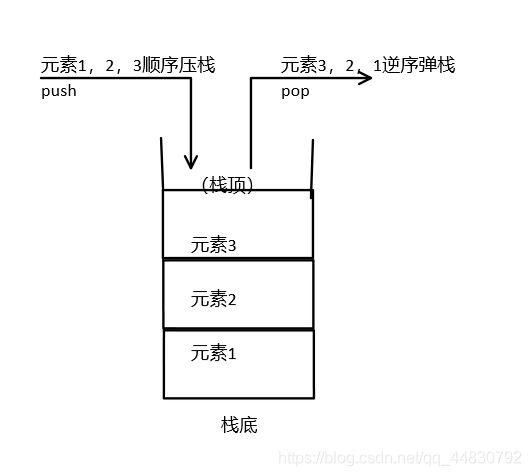
3、栈
基于以上两种结构,栈是一种具有【先进后出】的抽象特点数据结构,简单来说,它更像是一种只从一端进行存取操作的线性表,在栈顶加入元素操作称为压栈,在栈顶去除元素为弹栈,对于栈,基本的操作包括压栈(push)、弹栈(pop)、判空(isEmpty)、栈顶元素(getTop);
java中栈的使用可以直接使用Vector的子类Stack,也可以使用ArrayDeque,LinkedList等通过特定方法间接使用
出于性能调优一般不建议使用Stack,线程同步可使用Collections工具类中的synchronizedXxx()将线程不同步的ArrayDeque以及LinkedList转换成线程同步,ArrayDeque和LinkedList使用同数组和链表的选用;
Stack<String> stack = new Stack<>();
//压栈
stack.push("Stack");
stack.push("one");
stack.push("two");
//输出栈顶元素:此时为two
System.out.println(stack.peek());
//弹栈一次并再次输出栈顶元素和栈元素个数,后进先出,two被弹走了,栈顶为one
stack.pop();
System.out.println(stack.peek());
System.out.println(stack.size());
//清空栈
stack.clear();
//判断栈是否为空,上面清空,所以返回true
System.out.println(stack.isEmpty());
System.out.println("====================");
LinkedList<String> stack2 = new LinkedList<>();
//压栈
stack2.addFirst("stack");
stack2.addFirst("one");
stack2.addFirst("two");
//输出栈顶元素
System.out.println(stack2.getFirst());
//弹栈后输出栈顶元素和栈中元素个数
stack2.removeFirst();
System.out.println(stack2.getFirst());
System.out.println(stack2.size());
//清空栈
stack2.clear();
//判断栈是否为空 true
System.out.println(stack.isEmpty());
ArrayDeque<String> stack3 = new ArrayDeque<>();
/*ArrayDeque可以作为栈也可以当作队列,作为栈时方法同上,不在赘述,如
stack3.push("stack")或者stack3.addFirst("stack");
stack3.pop()或者stack3.removeFirst()*/
4、队列
队列是一种【先入先出】的引用数据结构,和栈相对,是从线性表的一端插入元素,另一端删除元素,允许插入的一端叫队尾,另一端是队头。基本操作同栈类似,只是删除的位置不一样。
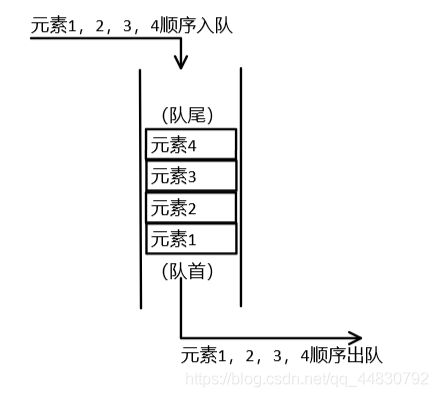
队列和栈一样,可以使用链表和数组实现,一般使用LinkedList充当队列
Queue<String> queue=new LinkedList<>();
//入队
queue.offer("obj1");
queue.offer("obj2");
queue.offer("obj3");
queue.offer("obj4");
//输出队列长度
System.out.println(queue.size());
//出队: 先入先出元素1出队
queue.poll();
//输出队头元素: 1走了,元素2是队头
System.out.println(queue.peek());
//清除队列后判断队列是否为空
queue.clear();
System.out.println(queue.isEmpty());
二、实现方法与原理
这里主要深入理解一下几种结构的构造,特性及原因,增删查改的方法实现
数组
构造:
数组由一块连续的内存空间组成,这块空间又被均等的划分为每一个元素,当知道第一个地址时,根据数学计算即可快速找到第i个元素的位置,所以数组的优点一下就表现出来,但对于计算机而言,一般一块大的连续地址空间较少(操作系统中有详细说明),所以不适合存储特别大的数据。这也是为什么对于未知的初始数据量一般采用链表而非数组。
下标是数组中重要的一部分,通过下标可以快速访问数组中的数据,之所以从0开始,原因是对于计算机而言,减法是双位数运算,若从1开始,每一步要减一,会降低效率。
需要注意的是,对于java中数组来说,数组不是一个基本数据类型,而是一个引用数据类型,即内存地址在JVM的堆内存区。变量中存的是地址而不是值。
可变数组(基于ArrayList)
首先创建了一个长度为0的数组,当添加第一个元素的时候,初始化容量10。也可以用new ArrayList(int initialCapacity)指定容量 。定义一个size记录数组长度,一个capacity记录数组容量。
添加:
添加元素到数组的末尾只需要添加到size下标处,若要添加元素到指定的位置,则需要把数组的包括指定下标往后的数据依次退一格,然后将指定下标处的值赋予新元素值.
每次添加元素时进行一次判断,如果数组的长度等于其容量,进行一次扩容,每次扩容为原来的1.5倍。(创建一个新数组,然后将原数组的元素拷贝到新数组)。 不难发现每一次扩容都需要新建数组,频繁的new对象和回收不用的旧数组,由于JVM垃圾回收机制,会浪费很多性能,因而尽可能少扩容,即初始化一个合适的容量。
删除
在删除数组中的元素时需要将指定下标的后的元素依次向前移动一个位置,
然后数组size–;

由上面的可以看出,数组的非尾部增加删除元素,时间耗费主要在移动数组元素上,移动的个数取决于插入位置。若表长为n,上述两种算法的时间复杂度达到了O(n),故常说数组的增删效率较低。
查找和修改
数组查找元素,直接根据下标,即可快速找到元素位置并进行修改,这取决与数组的构造。

public class MyArrayList {
//声明一个Object类型的数组
private Object[] elements;
//数组长度
private int size;
//无参构造函数,初始化数组容量为10
public MyArrayList() {
elements = new Object[10];
}
//有参构造方法,实现数组容量的初始化,用于指定容量
public MyArrayList(int initialCapacity) {
elements = new Object[initialCapacity];
}
//增加元素
public void add(Object obj) {
//首先,判断数组是否装满,是则扩容
if (size == elements.length-1) {
elements=growArray(elements);
}
elements[size++] = obj;
}
public void add(int index, Object obj) {
if (size == elements.length) {
elements=growArray(elements);
}
for (int i = index; i < size+1 ; i++) {
elements[i+1]=elements[i];
}
elements[index] = obj;
size++;
}
public Object[] growArray(Object[] elements){
//创建一个新数组,新容量为旧容量2倍
Object[] newArray = new Object[2 * size+1];
//将老数组拷贝到新数组内
System.arraycopy(elements, 0, newArray, 0, elements.length);
return newArray;
}
//删除指定下标对象,删除某位置,相当于 将后往前挪:
public void remove(int index) {
for (int i = index; i < size ; i++) {
elements[i]=elements[i+1];
}
size--;
/* 另一种实现
int numMoved = size - index - 1;
if (numMoved > 0) {
System.arraycopy(elements, index + 1, elements, index, numMoved);
}*/
}
//根据数据删除
public void remove(Object obj) {
for (int i = 0; i < size; i++) {
if (get(i).equals(obj)) {
remove(i);
}
}
}
//获取指定下标元素
public Object get(int index) {
return elements[index];
}
//修改指定下标元素
public void set(int index,Object obj){
elements[index] = obj;
}
//查看数组长度
public int size() {
return size;
}
}
链表
构造
链表由一个个节点组成,节点由数值域和指针域组成,每个节点占用不同的地址(可以不连续),仅靠一个指针域与其它节点产生联系,这种构造使链表在删除时和增加时有很大优势。但由于节点地址是随机的,因此查找不能想数组一样通过数学表达式计算,只能遍历节点查找指定的index;导致其查询修改效率不高;
双向链表具体构建
一种简单思路是可以设置虚拟的头节点head和尾节点rear,然后根据指针域的操作,可以在头尾节点间插入不同的节点以记录数据;
添加和删除
链表的添加元素仅仅需要把插入元素前的next指针指向自己,然后将自己的指针next指向下一个元素;
删除元素把前一个元素的next指针指向下一个元素即可;因为不涉及到其他元素的移动,只有自己前后元素有影响,所以效率高于数组。双向链表则需要更改两个指针域pre和next;

查找和修改
链表的查找比较麻烦,想要知道第i个元素,必须从头指针开始一直向后寻找到第i个next,找到之后才能修改,双向链表可以反向查找,比单链表会好一点,但依旧不如数组;
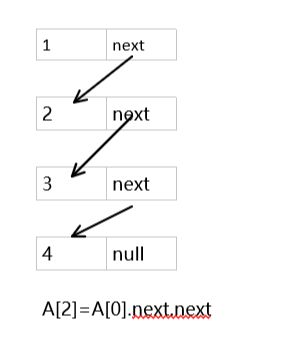
LinkedList的实现
public class MyLinkedList {
//头节点
LinkedListnode head;
//尾节点
LinkedListnode rear;
int size;
public int size() {
return size;
}
//这里为了方便实现直接构建了两个虚拟的节点,不计入size中
public MyLinkedList() {
head = new LinkedListnode(0);
rear = new LinkedListnode(0);
size = 0;
}
//获取指定节点值
public Object get(int index) {
if (index < 0 || index > size - 1) {
return -1;
}
//这里需要遍历节点以得到所求索引值
return getNode(index).val;
}
//获取链表的节点
private LinkedListnode getNode(int index) {
LinkedListnode temp = head.next;
for (int i = 0; i < index; i++) {
temp = temp.next;
}
return temp;
}
//在链表的第一个元素之前添加一个值为 val 的节点。插入后,新节点将成为链表的第一个节点。
public void addAtHead(Object val) {
//第一次添加
if (head.next == null) {
LinkedListnode newHead = new LinkedListnode(val);
head.next = newHead;
rear.pre = newHead;
} else {
LinkedListnode oldHead = head.next;
LinkedListnode newHead = new LinkedListnode(val);
newHead.pre = head;
newHead.next = oldHead;
head.next = newHead;
oldHead.pre = newHead;
}
size++;
}
//将值为 val 的节点追加到链表的最后一个元素。
public void addAtTail(int val) {
//第一次添加
if (rear.pre == null) {
LinkedListnode newHead = new LinkedListnode(val);
newHead.pre = head;
newHead.next = rear;
head.next = newHead;
rear.pre = newHead;
} else {
LinkedListnode oldTail = rear.pre;
LinkedListnode newTail = new LinkedListnode(val);
newTail.next = rear;
newTail.pre = oldTail;
oldTail.next = newTail;
rear.pre = newTail;
}
size++;
}
//在链表中的第index个节点之前添加值为val的节点。如果index等于链表的长度,则该节点将附加到链表的末尾。
// 如果 index 大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。
public void addAtIndex(int index, int val) {
// 如果 index 大于链表长度,则不会插入节点。
if (index > size) {
return;
//如果 index 等于链表的长度,则该节点将附加到链表的末尾。
} else if (index == size) {
addAtTail(val);
// 如果index小于0,则在头部插入节点。
} else if (index < 0) {
addAtHead(val);
//插到中间的情况
} else {
LinkedListnode oldNode = getNode(index);
LinkedListnode oldNodePre = oldNode.pre;
LinkedListnode newNode = new LinkedListnode(val);
newNode.pre = oldNodePre;
newNode.next = oldNode;
oldNode.pre = newNode;
oldNodePre.next = newNode;
size++;
}
}
//如果索引 index 有效,则删除链表中的第 index 个节点。
public void deleteAtIndex(int index) {
//index无效
if (index < 0 || index > size - 1 || size <= 0) {
return;
}
//要删除的节点
LinkedListnode node = getNode(index);
LinkedListnode nodePre = node.pre;
LinkedListnode nodeNext = node.next;
nodePre.next = nodeNext;
nodeNext.pre = nodePre;
size--;
}
public static void main(String[] args) {
MyLinkedList list=new MyLinkedList();
list.addAtTail(1);
list.addAtTail(2);
list.addAtTail(3);
list.addAtTail(4);
list.addAtTail(5);
list.addAtTail(6);
list.deleteAtIndex(5);
System.out.println(list.size());
System.out.println(list.get(4));
}
}
class LinkedListnode {
//节点前指针域
LinkedListnode pre;
//节点指针域
LinkedListnode next;
//数据
Object val;
public LinkedListnode(Object val) {
this.val = val;
}
}
栈
构造与实现
栈可以由数组(顺序栈),链表实现(链式栈),实现【后进先出】的特性,可以增加一个top指针,通过top的合理操作实现,为栈预设一个基本容量,当栈的空间不够使用时进行扩容,使用size变量记录栈大小。

注意:在弹栈和取栈顶元素时要先判空。
压栈和弹栈
以顺序栈为例,压栈时top指针自加1,指向新元素,返回新元素;弹栈时top自减1,这样top可以一直指向栈顶元素,返回删除的top加一元素;
栈顶元素
top指向即为栈顶元素,返回数组的top下标
判空
top=0时栈为空
清空栈
top归零返回一个新数组即可
基本操作如上,具体细节见代码,以顺序栈为例
public class MyStack {
// 向栈当中存储元素,存到栈中,就表示存储到数组中。
// Object类型数组,这里测试用,类型不固定
private Object[] elements;
// 栈帧,永远指向栈顶部元素
private int top;
//无参数构造方法。默认初始化栈容量10.是容量而非栈的大小;后面可扩容。
public MyStack() {
// 默认初始化容量是10.
this.elements = new Object[10];
// 给栈帧初始化
this.top = -1;
}
//指定容量的有参初始构造
public MyStack(int capacity) {
// 默认初始化容量是10.
this.elements = new Object[capacity];
// 给top初始化
this.top = -1;
}
//压栈
public void push(Object obj){
if(top >= elements.length - 1){
//扩容
elements=grow(elements);
}
// 向栈中加1个元素,栈帧向上移动一个位置。
top++;
elements[top] = obj;
//压栈测试
// System.out.println("压栈" + obj + "元素成功,栈帧指向" + index);
}
public int size(){
return top+1;
}
private Object[] grow(Object[] elements) {
Object[] newE;
newE = Arrays.copyOf(elements,elements.length*2);
return newE;
}
//弹栈
public Object pop() throws MyStackOperationException {
if(top < 0){
throw new MyStackOperationException("弹栈失败,栈已空!");
}
// System.out.print("弹栈" + elements[index] + "元素成功,");//弹栈测试
// 栈帧向下移动一位。
top--;
//返回为删除值
return elements[top +1];
}
//判空
public boolean isEmpty(){
//栈帧为-1 时栈空
if(top <0){
return true;
}
return false;
}
//取栈顶元素
public Object peek() throws MyStackOperationException {
if(top < 0){
throw new MyStackOperationException("弹栈失败,栈已空!");
}
return elements[top];
}
//清空栈
public void clear(){
//重构一次
this.elements = new Object[10];
this.top = -1;
}
public Object[] getElements() {
return elements;
}
public void setElements(Object[] elements) {
this.elements = elements;
}
public int getTop() {
return top;
}
public void setTop(int top) {
this.top = top;
}
}
//自定义栈空异常
class MyStackOperationException extends Exception{
public MyStackOperationException(){
}
public MyStackOperationException(String s){
super(s);
}
}
队列
构造
队列也可以使用两种结构实现,为了实现队列的【先入先出】特点,可以采用两个指针front,rear,分别在两端实现元素的增删;但事实上,对于链式存储,我们仅仅需要一个start指针记录队头。
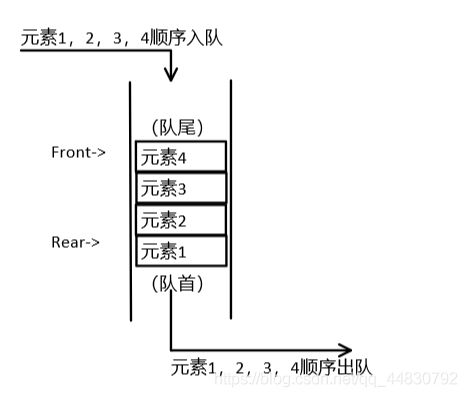
增加
队列增加元素,向链表尾部存入元素即可。元素会存储在链表中。
删除
删除元素,需要上文提到的start队头指针,链表数据没有删除,但用于记录队头的指针向后移,即实现了队列的删除

public class MyQueue {
// 数据
private final List<Object> data;
// 头指针
private int pStart;
private int size;
public MyQueue() {
//链表实现
data = new LinkedList<>();
pStart = 0;
size = 0;
}
//入队
public void enQueue(int x) {
data.add(x);
size++;
}
//出队
public void deQueue() {
//判空
if (isEmpty()) {
return;
}
pStart++;
size--;
}
//取得队头元素
public Object front() {
return data.get(pStart);
}
//判空
public boolean isEmpty() {
return pStart >= data.size();
}
public int size(){
return size;
}
public List<Object> getData() {
return data;
}
public int getpStart() {
return pStart;
}
public void setpStart(int pStart) {
this.pStart = pStart;
}
public int getSize() {
return size;
}
public void setSize(int size) {
this.size = size;
}
public static void main(String[] args) {
MyQueue q = new MyQueue();
q.enQueue(5);
q.enQueue(3);
if (!q.isEmpty()) {
System.out.println(q.front());
}
q.deQueue();
if (!q.isEmpty()) {
System.out.println(q.front());
}
q.deQueue();
if (!q.isEmpty()) {
System.out.println(q.front());
}
}
}
三、常见使用算法
数组
数组的应用非常广泛,由于其特性常出现在各种环境下,其索引结构也常用于字符串问题的解决。在使用的时候我们常常要对数组进行各种操作,下面简要说常用的.
1、排序
这里的排序一般是针对数字和字母。数组的排序方式有很多,如,选择排序,冒泡排序,插入排序等;事实上java提供了Arrays工具类的排序sort方法,这个排序算法是Vladimir Yaroslavskiy、Jon Bentley和Joshua Bloch的双轴快速排序。此算法在所有数据集上提供O(n log(n))性能,通常比传统的(单轴)快速排序实现更快。
这个算法效率很优秀,但我没有单独实现(。。。)
下面三种算法平均时间复杂度均有O(n^2),快速排序时间平均复杂度为O(nlog(2n))
冒泡排序
1、每一次循环结束之后,都要找出最大的数据,放到参与比较的这堆数据的最右边。(冒出最大的那个气泡。)
2、核心:
拿着左边的数字和右边的数字比对,当左边 > 右边的时候,交换位置。

//循环长度减一次
for(int i = arr.length-1; i > 0; i--){
for(int j = 0; j < i; j++){
// 不管是否需要交换位置,总之是要比较一次的。
//count++;//记录比较次数
if(arr[j] > arr[j+1]){
// 交换位置。
// arr[j] 和 arr[j+1] 交换
int temp;
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
//count2++;//交换位置的次数
}
}
}
选择排序
1、每一次从这堆“参与比较的数据当中”找出最小值,
2、拿着这个最小值和“参与比较的这堆最前面的元素”交换位置。
选择排序比冒泡排序好在:每一次的交换位置都是有意义的。
for(int i = 0; i < arr.length - 1; i++){
// 假设起点i下标位置上的元素是最小的。
int min = i;
for(int j = i+1; j < arr.length; j++){
if(arr[j] < arr[min]){
min = j; //最小值的元素下标是j
}
}
// 当i和min相等时,表示最初猜测是对的。
// 当i和min不相等时,表示最初猜测是错的,有比这个元素更小的元素,
// 需要拿着这个更小的元素和最左边的元素交换位置。
if(min != i){
// 表示存在更小的数据
// arr[min] 最小的数据
// arr[i] 最前面的数据
int temp;
temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
插入排序
1、将已排好的数组(没有就从第一个)和未排好的数组分开
2、从未排好的数组取出元素与前面的数组依次比较,找到自己的位置
···
for (int i = 0; i < arr.length - 1; i++) {
// 待插入的元素暂存到value.
int value = arr[i + 1];
int j = i;
// j < 0 时退出循环,说明 j 是最小的元素的索引值。
// 或者 arr[j] <= value 时退出循环,说明 j 是比value小的元素的索引值。
for (; j >= 0 && arr[j] > value; j--) {
// 把元素往后挪。
arr[j + 1] = arr[j];
}
// 把待插入元素,放到正确位置。
arr[j + 1] = value;
}
快速排序
1、先从数组中取出一个数作为基准数;
2、分区过程中比他大的放右边,比他小的放左边
3、对左右区间分别重复2操作,直到只剩一个数

private static void quickSort(int[] arr){
quickSort(arr,0,arr.length-1);
}
private static void quickSort(int[] arr, int left, int right) {
//如果left等于right,即数组只有一个元素,直接返回
if(left>=right) {
return;
}
//设置最左边的元素为基准值
int key=arr[left];
//数组中比key小的放在左边,比key大的放在右边,key值下标为i
int i=left;
int j=right;
while(i<j){
//j向左移,直到遇到比key小的值
while(arr[j]>=key && i<j){
j--;
}
//i向右移,直到遇到比key大的值
while(arr[i]<=key && i<j){
i++;
}
//i和j指向的元素交换
if(i<j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}
arr[left]=arr[i];
arr[i]=key;
quickSort(arr,left,i-1);
quickSort(arr,i+1,right);
}
2、查找
数组针对某元素的查找一般采用二分查找,事实上,由许多更好的查找算法,如插值查找、分块查找。
简单提一下顺序查找,所谓顺序查找,即遍历数组找到想要的元素
二分查找
1、每次取数组的中间值与查找值比较,若等于则查找到结果,
2、大于去右边数组执行1,小于则取左边数组执行1
3、当取得的数组只有一个元素或者查找到结果结束。

//arr为数组,dest为查找值
public static int binarySearch(int[] arr, int dest) {
// 开始下标
int begin = 0;
// 结束下标
int end = arr.length - 1;
// 开始元素的下标只要在结束元素下标的左边,就有机会继续循环。
while(begin <= end) {
// 中间元素下标
int mid = (begin + end) / 2;
if (arr[mid] == dest) {
return mid;
} else if (arr[mid] < dest) {
// 目标在“中间”的右边
// 开始元素下标需要发生变化(开始元素的下标需要重新赋值)
begin = mid + 1; // 一直增
} else {
// arr[mid] > dest
// 目标在“中间”的左边
// 修改结束元素的下标
end = mid - 1; // 一直减
}
}
return -1;
}
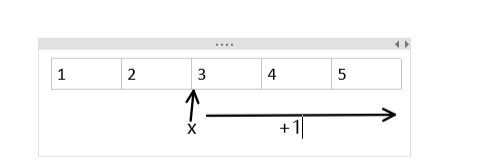
3、双指针的应用
在解决实际问题时,我们可以将数组的指针设置为两个,甚至多个;
但最常用的还是双指针,两种常用的方法如下图
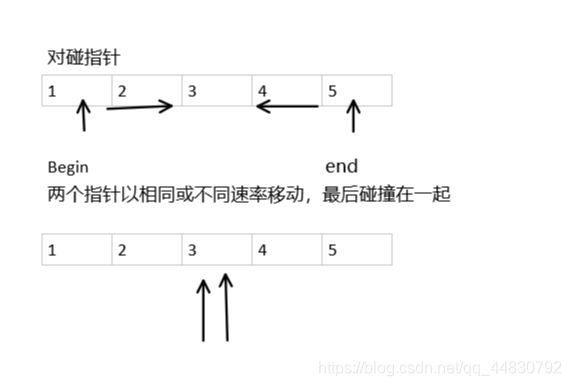

这个需要在题库中多练习一些才能可以熟练使用。
链表
链表的应用也很多,常用方法为虚拟节点,双指针,下面以问题引入算法应用。
1、链表逆序
举个例题,对于一个以head为头节点的链表将其逆序,且不允许申请额外空间。

链表的逆序通常有两个常用思路:递归和迭代,
1、递归常常用反复调用函数自己体现,对于链表逆序来说,这个函数需要做到1需要递归足够的次数满足题意,即参数几乎要覆盖链表,2调用一次函数更改一次节点的指向。3终止条件为节点为空。这个稍微不太好理解,具体见代码
2是双指针的思想,对于一个链表的逆序,定义两个指针,pre和cur前后指针,pre指向head前的null,cur指向head,对两个指针进行遍历,,每移动一次将cur的next指向pre;每遍历一个节点则逆置一个节点。

补充:如果没要求也可以用栈。将链表里的元素放进栈在出栈即可。
1,2实现:
public ListNode reverseList(ListNode head) {
//递归终止条件是当前为空,或者下一个节点为空,函数条件3
//head.next == null,这是为了找出链表的最后一个节点。
//另外一个条件是终止递归。
if(head==null || head.next==null) {
return head;
}
//这里的cur如果不是最后一个节点,就会重新调用直到是最后一个节点
//用这个可以满足函数条件1,
ListNode cur = reverseList(head.next);
//如果链表是 1->2->3->4->5,那么此时的cur就是5
//而head是4,head的下一个是5,下下一个是空
//所以head.next.next 就是5->4,函数条件二
//上面调用了4次这个函数,每次调用都会执行下面的语句。
//调用四次函数表面上都没执行完,每次后面的语句会存在java隐式栈中当上面结束了下面开始重新执行。根据栈后进先出,会根据head=4,3,2,1时执行下语句。
head.next.next = head;
//防止最终链表循环,需要将head.next设置为空
//因为上面5 -> 4,所以清除了原来的4 -> 5。
head.next = null;
//每层递归函数都返回cur,也就是最后一个节点
//这里其实是递归调用,并非固定值,尽管每轮cur都为5,但head一直在变
return cur;
}
public ListNode reverseList(ListNode head) {
//申请节点,pre和 cur,pre指向null
ListNode pre = null;
ListNode cur = head;
ListNode tmp = null;
while(cur!=null) {
//记录当前节点的下一个节点
tmp = cur.next;
//然后将当前节点指向pre
cur.next = pre;
//pre和cur节点都前进一位
pre = cur;
cur = tmp;
}
return pre;
}
2、链表求交点
对于两个链表a,b求其交点

两个思路
1、双指针同向移动。向两个链表a,b设置两个指针指向头节点,若a,b链表长度不相同,将长的链表指针向后移动|a.length-b.length|个单位,这时两个指针在同一起跑线上,同时同速度往后遍历,当指向节点相同时,找到交点。
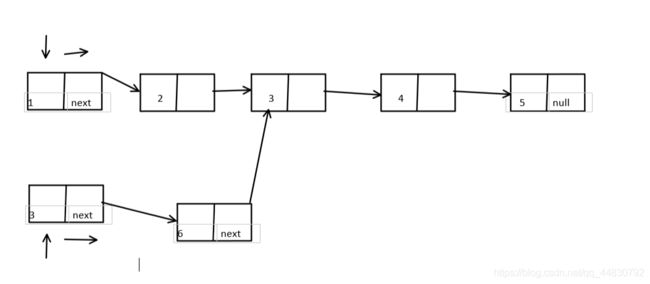
2、先把第一个链表的节点全部存放到集合set中,然后遍历第二个链表的每一个节点,判断在集合set中是否存在,如果存在就直接返回这个存在的结点。
3、链表求环
如图、求链表的环起始节点。
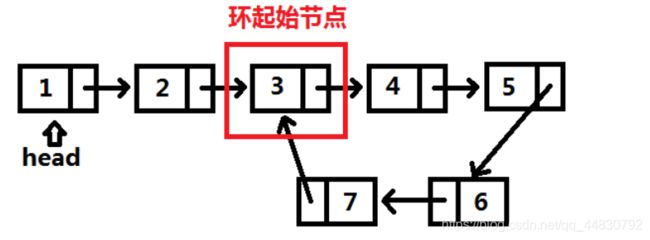
两个思路
1、使用集合set,遍历链表,加入集合set,只要在set中发现已有的节点,即为环起始节点。
2、快慢指针,fast和slow指针同时从起点出发,fast一次移动两格,slow一格,如果相遇,则有环。设相遇点为meet,则从meet与head头节点开始移动的两个同速指针的相遇点,就是环的起点。

4、链表归并
对于已排序的n个链表,求其合并后的头节点。要求,合并后依然有序。
思路
1、暴力合并,虚拟一个头节点,然后比较这n个链表的第i(i=0,1,2……)个元素,再插入head后面。
2、分治思想,这也是快排的思想核心,将链表间两两暴力合并,最后在合并。
3、使用集合TreeSet,将所有节点放进去在取出来连成链表。
5、链表划分
将链表以值x为界,大于x的放右边,反之放左边,不改变相对顺序。
思路
使用一个临时的虚拟节点,然后遍历,大的放右边,小的放左边。
栈和队列
下面这两种结构常由其特性而可以具体解决某些问题,
1、队列实现栈
两种方法(搬运自力扣225题)
两个队列
为了满足栈的特性,即最后入栈的元素最先出栈,在使用队列实现栈时,应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作,其中queue 1用于存储栈内的元素,queue 2作为入栈操作的辅助队列。
入栈操作时,首先将元素入队到 queue 2,然后将queue 1的全部元素依次出队并入队到queue 2,此时queue 2的前端的元素即为新入栈的元素,再将 queue 1 和 queue 2互换,则queue 1 的元素即为栈内的元素,queue 1的前端和后端分别对应栈顶和栈底。由于每次入栈操作都确保 queue 1 的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除 queue 1的前端元素并返回即可,获得栈顶元素操作只需要获得queue 1 的前端元素并返回即可(不移除元素)。由于 \textit{用于存储栈内的元素,判断栈是否为空时,只需要判断 queue 1 是否为空即可。
使用一个队列时,为了满足栈的特性,即最后入栈的元素最先出栈,同样需要满足队列前端的元素是最后入栈的元素。
一个队列
入栈操作时,首先获得入栈前的元素个数 nn,然后将元素入队到队列,再将队列中的前 nn 个元素(即除了新入栈的元素之外的全部元素)依次出队并入队到队列,此时队列的前端的元素即为新入栈的元素,且队列的前端和后端分别对应栈顶和栈底。由于每次入栈操作都确保队列的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可,获得栈顶元素操作只需要获得队列的前端元素并返回即可(不移除元素)。由于队列用于存储栈内的元素,判断栈是否为空时,只需要判断队列是否为空即可。
2、栈与递归
3、栈实现计算器
用栈实现对字符串的计算,如"1+2+3"结果为6,"1*(2+3)"结果为5;
总结
本文主要记录了一下线性数据结构的基本原理和java中使用,文笔多有不足,文中有不足的希望可以指出。