堆--C语言实现数据结构

> 本期带大家一起用C语言实现堆

1、堆的概念

堆（Heap）是一种特殊的树状数据结构，它是一种完全二叉树。堆被广泛应用于优先队列、排序算法等领域。

堆的特点：

1. 堆分为最大堆和最小堆两种类型。最大堆中，父节点的值大于或等于其子节点的值；最小堆中，父节点的值小于或等于其子节点的值。
2. 在最大堆中，最大的元素总是位于根节点；在最小堆中，最小的元素总是位于根节点。
3. 堆不保证子节点之间的相对顺序。

堆的实现通常使用数组来表示，利用数组的索引关系来表示节点之间的父子关系。具体来说，数组中下标 i 处的元素，其左子节点的下标为 2i+1，右子节点的下标为 2i+2，父节点的下标为 i/2 （其中除法为整数除法）。

堆的应用：

1. 堆排序（Heap Sort）：使用堆进行排序的算法。
2. 优先队列（Priority Queue）：使用堆实现的一种数据结构，可以高效地获取最大或最小值。
3. 图算法中的 Dijkstra 最短路径算法和 Prim 最小生成树算法等都可以使用堆进行优化。

总之，堆是一种满足特定条件的二叉树数据结构，在计算机科学中具有重要的应用价值。

2、堆的结构

3、堆的实现

首先我们需要先知道左孩子的下标是奇数，右孩子的下标是偶数

根据概念推导：

左孩子下标 = 2 * 双亲下标 + 1

右孩子下标 = 2 * 双亲下标 + 2

双亲下标=（孩子下标-1）/2 —— 这个式子是向下取整的，左右孩子都适用

3.1 结构设计

通过代码块得知，堆的结构和顺序表以及前面的栈结构都是一样的

HeapDataType* a：指向堆中数据存储数组的指针。这个数组用于存储堆中的元素。
int size：当前堆中元素的数量。
int capacity：堆的容量，即数组a的总大小

typedef int HeapDataType;

typedef struct heap
{
	HeapDataType* a;

	int size;
	int capacity;
}Heap;

3.2 堆的初始化

堆的初始化也是很简单的，同之前的顺序表和栈的初始化相同

void HeapInit(Heap* php)
{

	assert(php);
	
	php->a = (HeapDataType*)malloc(sizeof(HeapDataType));

	if (php->a == NULL)
	{
		perror("malloc::fail");
		return;
	}
	php->capacity = 0;
	php->size = 0;
}

3.3 向上调整算法

向上调整算法（Upward Heapify）用于在堆中插入新元素后，调整堆的结构，以满足堆的性质

每当我们向堆中插入一个数据的时候，我们会根据此时数据的下标来进行向上调整，以达到堆的性质
根据下标求出这个的双亲下标，然后我们进行比较，如果满足堆的性质，就跳出循环
不然的话就一直向上调整比较，以达到堆的性质

void AdjustUp(HeapDataType* a, int child)
{

	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;
	}

}

3.4 向下调整算法

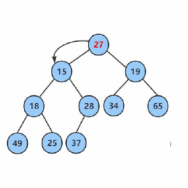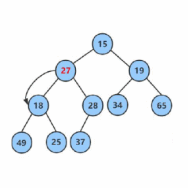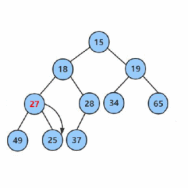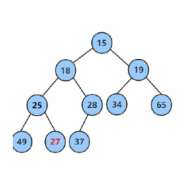
向下调整算法（Downward Heapify）用于在堆中删除根节点或者修改根节点的值后，调整堆的结构，以满足堆的性质

向下调整算法的话，如果要进行向下调整，那么必须得先保证左右子树都是堆，都满足堆的性质

向下调整算法的话可以用来建堆，还可以用来堆排序

首先我们根据当前节点的个数算出下标，然后根据最后一个元素的下标算出他的父节点，然后从这个父节点进行调整，保证满足堆的性质

然后叶子节点可以看作是一个堆

找出左右节点当中最小的那一个（小堆），然后再判断是否满足堆的性质，如果不满足，就调整

void AdjustDown(HeapDataType* a, int n, int parent)
{

	//前提是 左 右 子 树是一个堆

	int child = parent*2 + 1;

	while (child < n)
	{
		if (child + 1 < n && a[child] > a[child + 1])
			child++;

		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);

			parent = child;
			child = parent * 2 + 1;

		}
		else
			break;
	}
}

3.5 插入数据

插入数据的话，先判断是否需要扩容，然后将数据插入到数组有效数据的下一个位置，然后再根据向上调整算法进行调整

void HeapPush(Heap* php, HeapDataType x)
{
	assert(php);

	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HeapDataType* tmp = realloc(php->a, newcapacity * sizeof(HeapDataType));

		if (tmp == NULL)
		{
			perror("realloc::fail");
			return;
		}

		php->a = tmp;
		php->capacity = newcapacity;

	}
	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size-1);

	
}

3.6 删除数据

删除数据的话，一般是删除堆顶的数据，但是删除堆顶的数据之后，左右子树就相当于没有了父节点
那么，我们可以先让堆顶的数据和堆尾的数据先进行交换，让size–
然后再根据向下调整算法调整，此时左右子树已经构成了堆
根据向下调整算法的话可以很快地调整

void HeapPop(Heap* php)
{
	assert(php);

	assert(!HeapEmpty(php));

	Swap(&php->a[0], &php->a[php->size - 1]);

	php->size--;

	AdjustDown(php->a, php->size, 0);
}

3.7 堆顶数据

先判断一下堆当中是否有数据
有的话就返回下标为0的数据

HeapDataType HeapTop(Heap* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];

}

3.8 判断堆是否为空

bool HeapEmpty(Heap* php)
{
	assert(php);

	return php->size == 0;
}

3.9 销毁堆

销毁堆也很简单，直接上代码

void HeapDestroy(Heap* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

4、感谢与交流✅

如果大家通过本篇博客收获了,对堆有了新的了解的话
那么希望支持一下哦如果还有不明白的，疑惑的话，或者什么比较好的建议的话，可以发到评论区，
我们一起解决，共同进步 ❗️❗️❗️
最后谢谢大家❗️❗️❗️