快排算法(分治法)
一:什么是快排
相信很多人接触到的第一个排序就是冒泡排序,冒泡排序是一种拿一个数依次和后面进行比较,这样也就确保了每一次排序之后不论降序还是升序这一个数都会在末尾或者最前端,那么今天我们要将的是快速排序,基于冒泡排序的改进版本,为什么说是改进呢。要说冒泡排序是一个数都所有的数进行比较,那么快排就是将一组数分成大小两堆,然后在按照这种方法去分,知道保证只剩下一个数,这样也就保证了它是有序的了,接下里我们一起看一下他的实现原理及过程。
二:实现过程
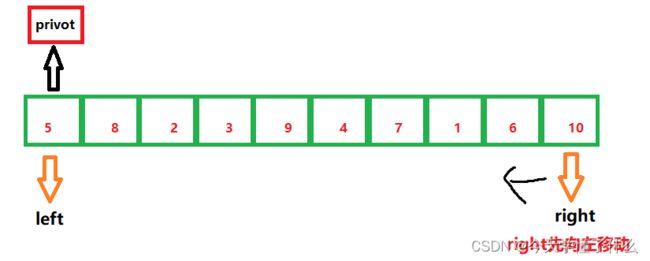
快排又称为挖坑排序发,具体是什么意思呢。首先我们给定一个数组,这个数可以是数组中任意选定的一个数,假定我们选择的这个数就是第一个数我们设他为privot,然后在给定一个左下标和右下标(设为left为小堆和right为大堆),再用两个变量来保存当前left和right的值(设为L&&R),然后left和right依次往中间移动,
设我们先移动right指向的数,如果遇到的数>=privot我们就不用管他,直到遇到了小于privot的数我们就停止对right的移动。
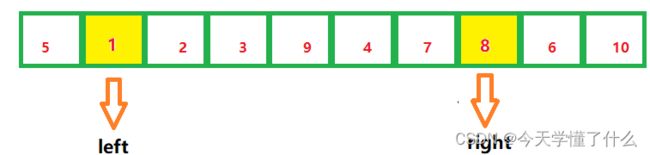
当right找到了比privot小的数我们就停止对他的移动,然后移动我们的left,同理,如果left遇到的数小于privot我们就不用管,直到遇到大于privot的数就停止。这个时候我们就找了第一次需要交换位置的两个元素,我们可以用空瓶子的原理交换也可以运用加法或者异或,交换的方法有很多这里就不一一列举了。
当我们交换了这个元素的位置之后就得到一个这样一个数组了
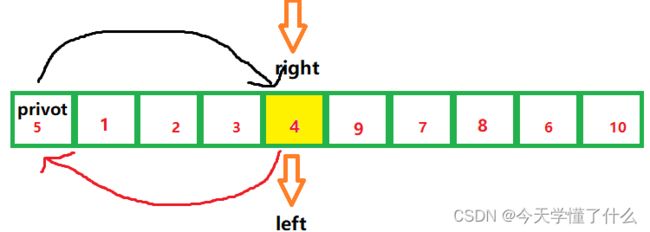
然后我们就可以重复这样的步骤,最后一直到left和right都指向同一个元素的时候也就是没有元素在可以进行比较交换了,我们这个时候就可以把我们的privot这个数放在这个位置
交换之后的数组就变成了左边全是小于privot的数,右边全是大于privot的数
如果我们认真看就会发现循环一次之后的privot刚好是在本来应该存在的位置 。这样我们就完成了第一个数的排序。
小堆的排序:这个时候我们就可以把从privot的数分开作为小,大堆。设我们接下来需要对小堆进行排序,对小堆进行排序的话也就是当前的右下标指向的值不能超过privot,我们就可以让右下表指向right-1的位置,然后再把L和right-1再传给这个函数它继续对剩下的值进行排序,当最后只有一个数的时候我们认为它就是有序的。
大堆的排序:同理大堆就是全部都是大于privot的数,我们就可以让left+1设为开始的坐下标,又下标为R,然后当只剩最后一个数的时候同样它也是有序的。
三:总结
1:从数组中任意找出一个数作为基数,设置左右下标依次移动,当right遇到的数小于privot就停止移动,left遇到大于privot的数也停止移动,然后交换这两个数。
2:当左右下标都指向同一个值的时候就把privot和这个数交换
3:重复上面的步骤
void quicksort(int arr[], int left, int right) //快排
{
//保存当前left,right位置
int L = left;
int R = right;
//用第一个元素作为基点
int privot = arr[L];
while (L < R)
{
while (L < R && arr[R] >= privot)
{
R--; //5,6,8,1,4,3,9,2,7,10
}
while (L < R && arr[L] <= privot)
{
L++;
}
//如果L指向的元素大于R指向的元素就交换他们的值
if (arr[L] > arr[R])
{
int tmp = arr[L];
arr[L] = arr[R];
arr[R] = tmp;
}
}
//将L指向的值非起始位置
arr[left] = arr[L];
//在将privot的值放在L的位置
arr[L] = privot;
//以L为起点的地方到L-1的地方分为小堆
quicksort(arr, left, L-1);
//以L+1的地方到right分为大堆
quicksort(arr, L+1, right);
}
int main()
{
int arr[10] = { 5,6,8,1,4,3,9,2,7,10 };
int left = 0;
int right = sizeof(arr) / sizeof(arr[0])-1;
quicksort(arr, left, right);
int i = 0;
for (i = 0; i < 10; i++)
{
printf("%d", arr[i]);
}
}