Hankel矩阵法进行系统辨识
脉冲响应法(impulse response method)是指线性系统在零初始条件输入脉冲信号后输出的瞬态响应,即输出响应叫脉冲响应。建立系统的非参数模型来观测系统的脉冲响应,以求得系统数学模型的待定参数,进而实现系统辨识的目的。利用脉冲响应创建Hankel矩阵,可以实现对系统进行辨识。
现需对三阶系统 G ( s ) = b 0 s + b 1 a 0 s 3 + a 1 s 2 + a 2 s + a 3 G(s)= \frac{b_0s+b_1}{a_0s^3+a_1s^2+a_2s+a_3} G(s)=a0s3+a1s2+a2s+a3b0s+b1利用Hankel矩阵法进行辨识,并将辨识结果与原系统进行比较分析,其中 b 0 = 1 , b 1 = 15 , a 0 = 1 , a 1 = 5 , a 2 = 4 , a 3 = 15 。 b_0=1,b_1=15,a_0=1,a_1=5,a_2=4,a_3=15。 b0=1,b1=15,a0=1,a1=5,a2=4,a3=15。
Hankel算法介绍
Hankel矩阵是指每一条逆对角线上的元素都相等的矩阵,其在数字信号处理、数值计算、系统控制等领域均有广泛的应用。
我们假设有一n阶传递函数:
G ( z − 1 ) = b 1 z − 1 + b 2 z − 2 + ⋯ + b n z − n 1 + a 1 z − 1 + a 2 z − 2 + ⋯ + a n z − n G(z^{-1})= \frac{b_1z^{-1}+b_2z^{-2}+{\cdots}+b_nz^{-n}}{1+a_1z^{-1}+a_2z^{-2}+{\cdots}+a_nz^{-n}} G(z−1)=1+a1z−1+a2z−2+⋯+anz−nb1z−1+b2z−2+⋯+bnz−n其相应的状态方程可以写为: { x ( k + 1 ) = A x ( k ) + b u ( k ) y ( k ) = c x ( k ) \left\{\begin{array}{l} x(k+1)=A x(k)+b u(k) \\ y(k)=c x(k) \end{array}\right. {x(k+1)=Ax(k)+bu(k)y(k)=cx(k)其脉冲传递函数又可以写为: G ( z − 1 ) = c ( z I − A ) − 1 b G\left(z^{-1}\right)=c(z I-A)^{-1} b G(z−1)=c(zI−A)−1b对应的单位脉冲响应为: g ( k ) = c A k − 1 b g(k)=c A^{k-1} b g(k)=cAk−1b下面我们进行推导Hankel矩阵。
因为:
( I − A z ) ∑ i = 0 ∞ ( A z ) i = ∑ i = 0 ∞ ( A z ) i − ∑ i = 0 ∞ ( A z ) i + 1 = ( A z ) 0 + ∑ i = 0 ∞ ( A z ) i + 1 − ∑ i = 0 ∞ ( A z ) i + 1 = I + ∑ i = 0 ∞ ( A z ) i + 1 − ∑ i = 0 ∞ ( A z ) i + 1 = I \begin{gathered} \left(I-\frac{A}{z}\right) \sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i}=\sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i}-\sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i+1} \\ \quad=\left(\frac{A}{z}\right)^{0}+\sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i+1}-\sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i+1} \\ \quad=I+\sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i+1}-\sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i+1}=I \end{gathered} (I−zA)i=0∑∞(zA)i=i=0∑∞(zA)i−i=0∑∞(zA)i+1=(zA)0+i=0∑∞(zA)i+1−i=0∑∞(zA)i+1=I+i=0∑∞(zA)i+1−i=0∑∞(zA)i+1=I所以:
( I − A z ) ∑ i = 0 ∞ ( A z ) i = I ⇒ z I − A z ∑ i = 0 ∞ ( A z ) i = I ⇒ ∑ i = 0 ∞ ( A z ) i = z z I − A = z ( z I − A ) − 1 \begin{array}{l} \left(I-\frac{A}{z}\right) \sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i}=I \Rightarrow \frac{z I-A}{z} \sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i}=I \\ \Rightarrow \sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i}=\frac{z}{z I-A}=z(z I-A)^{-1} \end{array} (I−zA)∑i=0∞(zA)i=I⇒zzI−A∑i=0∞(zA)i=I⇒∑i=0∞(zA)i=zI−Az=z(zI−A)−1则: ( z I − A ) − 1 = z − 1 ∑ i = 0 ∞ ( A z ) i = = A 0 z − 1 + A 1 z − 2 + A 2 z − 3 ⋯ \begin{array}{l} (z I-A)^{-1}=z^{-1} \sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i}= \\ =A^{0} z^{-1}+A^{1} z^{-2}+A^{2} z^{-3} \cdots \end{array} (zI−A)−1=z−1∑i=0∞(zA)i==A0z−1+A1z−2+A2z−3⋯则脉冲传递函数与脉冲响应的关系为: G ( z − 1 ) = c ( z I − A ) − 1 b = c z − 1 ∑ i = 0 ∞ ( A z ) i b = c A 0 b z − 1 + c A b z − 2 + c A 2 b z − 3 + ⋯ = g ( 1 ) z − 1 + g ( 2 ) z − 2 + g ( 3 ) z − 3 + ⋯ \begin{aligned} G\left(z^{-1}\right) &=c(z I-A)^{-1} b=c z^{-1} \sum_{i=0}^{\infty}\left(\frac{A}{z}\right)^{i} b \\ &=c A^{0} b z^{-1}+c A b z^{-2}+c A^{2} b z^{-3}+\cdots \\ &=g(1) z^{-1}+g(2) z^{-2}+g(3) z^{-3}+\cdots \end{aligned} G(z−1)=c(zI−A)−1b=cz−1i=0∑∞(zA)ib=cA0bz−1+cAbz−2+cA2bz−3+⋯=g(1)z−1+g(2)z−2+g(3)z−3+⋯则由 G ( z − 1 ) = b 1 z − 1 + b 2 z − 2 + ⋯ + b n z − n 1 + a 1 z − 1 + a 2 z − 2 + ⋯ + a n z − n b 1 z − 1 + b 2 z − 2 + ⋯ + b n z − n = G ( z − 1 ) ⋅ ( 1 + a 1 z − 1 + a 2 z − 2 + ⋯ + a n z − n ) b 1 z − 1 + b 2 z − 2 + ⋯ + b n z − n = ( g ( 1 ) z − 1 + g ( 2 ) z − 2 + g ( 3 ) z − 3 + ⋯ ) ⋅ ( 1 + a 1 z − 1 + a 2 z − 2 + ⋯ + a n z − n ) = g ( 1 ) z − 1 + ⋯ + [ g ( 2 ) + a 1 g ( 1 ) ] z − 2 + ⋯ + [ g ( n ) + ∑ i = 1 n − 1 g ( i ) a n − i ] z − n + [ g ( n + 1 ) + ∑ i = 1 n − 1 g ( i ) a n + 1 − i ] z − ( n + 1 ) + ⋯ + [ g ( 2 n ) + ∑ i = 1 2 n − 1 g ( i ) a 2 n − i ] z − 2 n \begin{array}{l} G\left(z^{-1}\right)=\frac{b_{1} z^{-1}+b_{2} z^{-2}+\cdots+b_{n} z^{-n}}{1+a_{1} z^{-1}+a_{2} z^{-2}+\cdots+a_{n} z^{-n}} \\ b_{1} z^{-1}+b_{2} z^{-2}+\cdots+b_{n} z^{-n}=G\left(z^{-1}\right) \cdot\left(1+a_{1} z^{-1}+a_{2} z^{-2}+\cdots+a_{n} z^{-n}\right) \\ b_{1} z^{-1}+b_{2} z^{-2}+\cdots+b_{n} z^{-n} \\ =\left(g(1) z^{-1}+g(2) z^{-2}+g(3) z^{-3}+\cdots\right) \cdot\left(1+a_{1} z^{-1}+a_{2} z^{-2}+\cdots+a_{n} z^{-n}\right) \\ =g(1) z^{-1}+\cdots+\left[g(2)+a_{1} g(1)\right] z^{-2}+\cdots+\left[g(n)+\sum_{i=1}^{n-1} g(i) a_{n-i}\right] z^{-n} \\ +\left[g(n+1)+\sum_{i=1}^{n-1} g(i) a_{n+1-i}\right] z^{-(n+1)}+\cdots+\left[g(2 n)+\sum_{i=1}^{2 n-1} g(i) a_{2 n-i}\right] z^{-2 n} \end{array} G(z−1)=1+a1z−1+a2z−2+⋯+anz−nb1z−1+b2z−2+⋯+bnz−nb1z−1+b2z−2+⋯+bnz−n=G(z−1)⋅(1+a1z−1+a2z−2+⋯+anz−n)b1z−1+b2z−2+⋯+bnz−n=(g(1)z−1+g(2)z−2+g(3)z−3+⋯)⋅(1+a1z−1+a2z−2+⋯+anz−n)=g(1)z−1+⋯+[g(2)+a1g(1)]z−2+⋯+[g(n)+∑i=1n−1g(i)an−i]z−n+[g(n+1)+∑i=1n−1g(i)an+1−i]z−(n+1)+⋯+[g(2n)+∑i=12n−1g(i)a2n−i]z−2n比较上式两边 z − 1 z^{-1} z−1的同幂方次项的系数,有Hankel矩阵H(n,1)
[ g ( 1 ) g ( 2 ) ⋯ g ( n ) g ( 2 ) g ( 3 ) ⋯ g ( n + 1 ) ⋯ g ( n ) g ( n + 1 ) ⋯ g ( 2 n − 1 ) ] [ a n a n − 1 ⋮ a 1 ] = − [ g ( n + 1 ) g ( n + 2 ) ⋮ g ( 2 n ) ] \left[\begin{array}{cccc} g(1) & g(2) & \cdots & g(n) \\ g(2) & g(3) & \cdots & g(n+1) \\ & & \cdots & \\ g(n) & g(n+1) & \cdots & g(2 n-1) \end{array}\right]\left[\begin{array}{c} a_{n} \\ a_{n-1} \\ \vdots \\ a_{1} \end{array}\right]=-\left[\begin{array}{c} g(n+1) \\ g(n+2) \\ \vdots \\ g(2 n) \end{array}\right] ⎣⎢⎢⎡g(1)g(2)g(n)g(2)g(3)g(n+1)⋯⋯⋯⋯g(n)g(n+1)g(2n−1)⎦⎥⎥⎤⎣⎢⎢⎢⎡anan−1⋮a1⎦⎥⎥⎥⎤=−⎣⎢⎢⎢⎡g(n+1)g(n+2)⋮g(2n)⎦⎥⎥⎥⎤及 [ b 1 b 2 ⋮ b n ] = − [ 1 0 ⋯ 0 a 1 1 ⋯ 0 ⋮ ⋮ ⋯ ⋮ a n − 1 a n − 2 ⋯ 1 ] [ g ( 1 ) g ( 2 ) ⋮ g ( n ) ] \left[\begin{array}{c} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{array}\right]= -\left[\begin{array}{cccc} 1 & 0 & \cdots & 0 \\ a_1 & 1 & \cdots & 0 \\ \vdots & \vdots & \cdots & \vdots\\ a_n-1 & a_n-2 & \cdots & 1 \end{array}\right]\left[\begin{array}{c} g(1) \\ g(2) \\ \vdots \\ g(n) \end{array}\right] ⎣⎢⎢⎢⎡b1b2⋮bn⎦⎥⎥⎥⎤=−⎣⎢⎢⎢⎡1a1⋮an−101⋮an−2⋯⋯⋯⋯00⋮1⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡g(1)g(2)⋮g(n)⎦⎥⎥⎥⎤最后即得到Hankel矩阵,根据上式即可计算得出辨识系统在离散域传递函数的系数,最后根据双线性法即可得到连续域的传递函数。
程序编写
根据前面对Hankel算法的介绍进行编写代码,其算法流程图如下所示。

首先我们对系统进行初始化,分别设置 a i 、 b i , a_i、b_i, ai、bi,输入 T 0 T_0 T0,接着求解原系统的离散方程,求出其脉冲响应进而构造Hankel矩阵H(3,1),根据前文公式进行求解辨识系统的离散域的传递函数系数,由双线性变换法求解辨识系统连续域的传递函数,最后绘制原系统与辨识系统的单位阶跃响应进行比较分析。完整代码如下:
clc;
clear all;
close all;
T0 = input('采样周期T0='); %手动输入采样周期
b0 = 1;
b1 = 15;
a0 = 1;
a1 = 5;
a2 = 4;
a3 = 15;
num = [b0 b1];
den = [a0 a1 a2 a3];
sys = tf(num,den);%sys为实际的传递函数
sysd = c2d(sys,T0);%传递函数离散化
%% 绘制原系统的单位脉冲响应
figure(1)
impulse(sysd)
grid on
[y,t] = impulse(sysd);
H = [y(2),y(3),y(4);y(3),y(4),y(5);y(4),y(5),y(6)];%构造Hankel矩阵
if det(H)==0
disp('Hankel矩阵奇异,无法求逆');
else
A = inv(H)*[-y(5);-y(6);-y(7)];
B = [1 0 0;A(3) 1 0;A(2) A(3) 1]*[y(2);y(3);y(4)];
numd = B';
dend = [1 A(3) A(2) A(1)];
bssysd = tf(numd,dend,T0); % 创建1个采样时间为T0的离散时间传递函数
end
bianshisys = d2c(bssysd,'tustin');%辨识出的传递函数
%% 绘制原系统与辨识系统的单位阶跃响应
figure(2)
step(T0*bianshisys,'g-')%特别注意需要乘T0,具体原因这里不做具体介绍
hold on
step(sys)
grid on
legend('辨识传递函数','实际传递函数');
%% 计算均方误差
t= 0 : T0 : 60;
y1= step(sys,t);
y2= step(T0*bianshisys,t);
delta_y = mean((y2 - y1).^2)
分别令 T 0 = 0.2 、 0.5 、 0.8 T_0=0.2、0.5、0.8 T0=0.2、0.5、0.8,对系统进行仿真运算,得到原系统与辨识系统的传递函数。分别对 T 0 = 0.2 、 0.5 、 0.8 T_0=0.2、0.5、0.8 T0=0.2、0.5、0.8各个时刻原系统与辨识系统进行单位阶跃响应曲线的绘制如下所示:
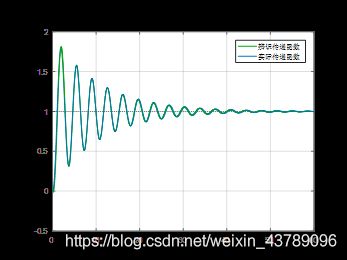
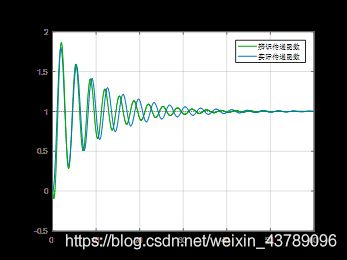
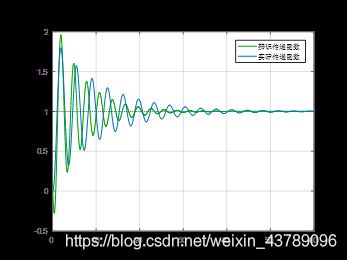
误差分析
分析上图可知,当 T 0 = 0.2 T_0=0.2 T0=0.2辨识系统与原系统的拟合程度最大,误差最小,辨识效果极好;当 T 0 = 0.5 T_0=0.5 T0=0.5辨识系统与原系统的拟合程度次之,误差次之,辨识效果中等;当 T 0 = 0.8 T_0=0.8 T0=0.8辨识系统与原系统的拟合程度最小,误差最大,辨识效果不佳,由此可见采样时间 T 0 T_0 T0越低,系统的辨识程度最高。我们可以对原系统与辨识系统的若干个时刻的值进行均方误差的计算:
MSE ( y ^ ) = E ( y ^ − y ) 2 \operatorname{MSE}(\hat{y})=E(\hat{y}-y)^{2} MSE(y^)=E(y^−y)2计算得到的结果如下表所示:
| T 0 T_0 T0 | MSE ( y ^ ) \operatorname{MSE}(\hat{y}) MSE(y^) |
|---|---|
| 0.2 | 0.00063061 |
| 0.5 | 0.0127 |
| 0.8 | 0.0399 |
由上表可以看出,随着 T 0 T_0 T0的增大, MSE ( y ^ ) \operatorname{MSE}(\hat{y}) MSE(y^)逐渐减小,分析其误差原因,一是采用双线性变化法其 s s s域和 z z z域有 w = 2 T tan w z T 2 w=\frac{2}{T} \tan \frac{w_{z} T}{2} w=T2tan2wzT的关系,带来严重的高频失真, s s s域角频率从 0 ∼ ∞ 0 \sim \infty 0∼∞的频段均压缩到 z z z域的有限频段 0 ∼ w s 2 = π T 0 \sim \frac{w_{s}}{2}=\frac{\pi}{T} 0∼2ws=Tπ上,低频性线性近似程度较好,高频段的压缩非线性;二是只有 g ( n ) g(n) g(n)在无穷多项时才完全等于 G ( z ) G(z) G(z)而我们只取了 n n n项,具有截断误差。