LeetCode 1235. 规划兼职工作--二分查找后进行动态规划
- 规划兼职工作
你打算利用空闲时间来做兼职工作赚些零花钱。
这里有 n 份兼职工作,每份工作预计从 startTime[i] 开始到 endTime[i] 结束,报酬为 profit[i]。
给你一份兼职工作表,包含开始时间 startTime,结束时间 endTime 和预计报酬 profit 三个数组,请你计算并返回可以获得的最大报酬。
注意,时间上出现重叠的 2 份工作不能同时进行。
如果你选择的工作在时间 X 结束,那么你可以立刻进行在时间 X 开始的下一份工作。
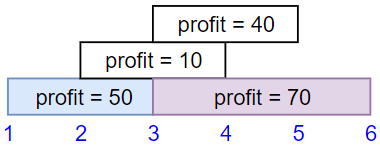
输入:startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出:120
解释:
我们选出第 1 份和第 4 份工作,
时间范围是 [1-3]+[3-6],共获得报酬 120 = 50 + 70。
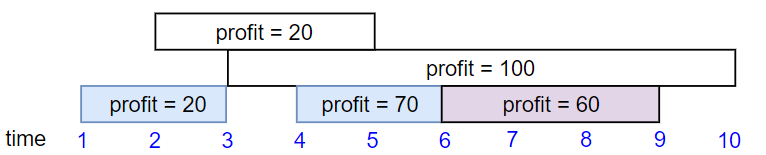
输入:startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出:150
解释:
我们选择第 1,4,5 份工作。
共获得报酬 150 = 20 + 70 + 60。
输入:startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出:6
提示:
1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
1 <= startTime[i] < endTime[i] <= 10^9
1 <= profit[i] <= 10^4
题解:
这个题目如果做过相关动态规划的题目可能比较熟悉,比如看看曾经codeforces的这个题目codeforces–D. Make The Fence Great Again–动态规划,这样分析,每个兼职只有两种状态,做或者不做,于是我们按每个兼职结束的时间进行排序,定义数组dp[maxn][2],针对排序后的数组,dp[i]表示从兼职0到兼职i经过得到的最大的收益,其中dp[i][0]表示不做兼职i,dp[i][1]表示要做兼职i。
于是最终的答案=max(dp[n][0],dp[n][1])。
那么就简单了,如果兼职i不做,也就是dp[i][0],那么就是比较上一个兼职得到的结果,就是
dp[i][0]=max(dp[i-1][0],dp[i-1][1]);
如果做呢?那就得考虑结束时间最接近兼职i开始时间的那个兼职pre[i],于是
dp[i][1]=max(dp[pre[i]][0]+profit[i],dp[pre[i]][1]+profit[i]);
不难理解吧,于是为了找到结束时间最接近兼职i开始时间的那个兼职pre[i],我们利用二分查找得到结果。
AC代码
class Solution {
public:
struct Node
{
int startTime,endTime,profit;
};
vector<Node>a;
static int cmp(Node a1,Node a2)
{
return a1.endTime<a2.endTime;
}
int pre[50010];
int fin_pre(int l,int r,int startTime)二分找结果
{
int fin=-1;
while(l<=r)
{
int mid=(l+r)/2;
if(a[mid].endTime<=startTime)
{
fin=mid;
l=mid+1;
}
else r=mid-1;
}
return fin;
}
int dp[50010][2];
int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
for(int i=0;i<startTime.size();i++)
{
Node t;
t.startTime=startTime[i];
t.endTime=endTime[i];
t.profit=profit[i];
a.push_back(t);
}
sort(a.begin(),a.end(),cmp);
memset(pre,-1,sizeof(pre));
for(int i=0;i<a.size();i++)
{
pre[i]=fin_pre(0,i,a[i].startTime);
}
memset(dp,0,sizeof(dp));
dp[0][1]=a[0].profit;
dp[0][0]=0;
for(int i=1;i<a.size();i++)
{
dp[i][0]=max(dp[i-1][0],dp[i-1][1]);//继承上一个
if(pre[i]!=-1)
dp[i][1]=max(dp[pre[i]][0]+a[i].profit,dp[pre[i]][1]+a[i].profit);
else dp[i][1]=a[i].profit;
}
return max(dp[a.size()-1][0],dp[a.size()-1][1]);
}
};