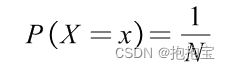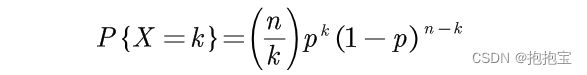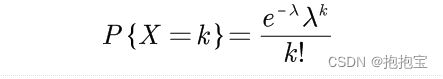金融中的数学:概率分布(上)
概率分布是描述随机变量可能取值的概率的函数。它可以用来描述离散变量和连续变量的概率分布。对于离散变量的概率分布,我们称其为离散概率分布。对于连续变量的概率分布,我们称其为连续概率分布。本文主要介绍离散型概率分布。
1.离散型均匀分布
离散型均匀分布是一种描述离散变量可能取值的概率分布,其中每个取值的概率是相等的。在离散型均匀分布中,变量取值的范围是有限的且连续的。
离散型均匀分布的概率质量函数如下:
其中,X 表示随机变量的取值,x 表示取值范围内的任意一个具体取值,N 表示取值范围内的元素个数。
举个例子来说明离散型均匀分布:假设有一个骰子,它有 6 个面,标有数字 1 到 6。每个面的出现概率是相等的,即 P(X = 1) = P(X = 2) = P(X = 3) = P(X = 4) = P(X = 5) = P(X = 6) = 1/6。这就是一个离散型均匀分布。
需要注意的是,离散型均匀分布仅适用于有限的取值范围。如果取值范围是无限的,就需要使用连续型均匀分布来描述概率分布。
可以使用如下python代码创建一个离散型均匀分布:
import random
print(random.randint(0,9))2.二项分布
二项分布(binomial distribution)是一种描述离散型随机变量在固定次数的独立重复试验中成功次数的概率分布。在每次试验中,随机变量只有两个可能的结果,通常用成功(S)和失败(F)表示。其中,成功的概率为 p,失败的概率为 1-p(或 q = 1-p)。
二项分布的概率质量函数(PMF)可以表示为:
其中,X 表示随机变量的取值,k 表示成功的次数,n 表示独立实验的总次数,C(n, k) 表示组合数(即从 n 次试验中取 k 次成功的组合数),p 表示每次实验成功的概率,(1-p)^(n-k) 表示失败的概率。
二项分布常用于描述具有二元结果的实验和事件,例如投硬币、抽样调查、生产线上的次品率等。它是概率论和统计学中最基本的概率分布之一,在许多领域都有广泛的应用。
可以使用如下python代码创建一个二项分布:
from numpy import randaom
x=random.binomial(n=10,p=0.9)
print(x)3.泊松分布
泊松分布(Poisson distribution)是一种描述事件在固定时间或空间区域内随机发生的概率分布。泊松分布适用于描述事件发生的次数的概率,例如在一段时间内发生的事故数量、在一定区域内发生的电话呼叫数量等。
泊松分布的概率质量函数(PMF)可以表示为:
其中,X 表示随机变量的取值,k 表示事件发生的次数,λ 表示在给定时间或空间区域内平均发生的事件次数,e 是自然对数的底数(约等于2.71828),k! 表示 k 的阶乘。
泊松分布的特点包括:
1. 事件在任意两个非重叠时间或空间区域内的发生是独立的。
2. 在相同的时间或空间区域内,事件的发生概率在区域大小上是相等的。
3. 事件的发生次数是离散的,取值范围是非负整数(0, 1, 2, ...)。
泊松分布常用于描述稀有事件或低发生率事件的统计分布,特别是当事件发生的平均次数固定且相对较小的情况。例如,可以使用泊松分布来估计每天发生的交通事故数量、机器故障次数、电话呼叫数量等。
在python中可以使用如下代码生成一个泊松分布
from numpy import random
x=random.poisson(lam=2,size=10)
print(x)