仰天倀笑

【体系结构】IEEE754浮点数标准学习与机器码表示总结

怎么上传了，排版和Typora差这么多…头疼，就这样吧…

一 IEEE754浮点数标准学习

没想到本科不喜欢、瞎学的祭祖，现在还是得重新、认真地重学一遍。“不喜欢”果然无法成为拒绝学习的理由，丢书时有多“硬气”，苦读时就有多“卑微” (￣▽￣)"…

IEEE754这块以前看课本，没看懂“表达式”，考研时直接放弃。今天捋起袖子，把这定点数和浮点数好好看一遍吧。

本篇不是小白入门，适合看完书后还有疑惑的情况下，来过一遍。

个人颜色标注习惯：

红色——大重点；

蓝色——对我重要的个人思考；

洋红色——自我Q/A环节，问句专用.

1 前期疑惑解答

先解答个人在查找IEEE754格式时，最大的疑惑：各资料上对IEEE754的位数记录不太一致，是我哪里没理解对么？

IEEE754文档

没看懂。虽然记录了完整内容，但混在一起写的，关于下面表格的信息没有明显区分标注出来，直接拔线投降——不看了。
祭祖（计组）课本

为什么感觉和SPEC上不一样？例如：书本上说，单精度32位，双精度64位；但网上说是24位、53位…
- 懂了，其实是一样的，只是省略描述时的对象不同。
  
  细说：IEEE754文档及其他讨论的文章，在描述位数时，描述的是“尾数位的有效位数” —— ①是指尾数；②是包含、计入了规格化后省略了、未存储的那个隐含位“1”，因此在要多一位（ $23\ bit \to 24\ bit$ ）。
网上的有效内容

挺好的一个表格，我先粗糙的扣下来：
- “有效位”表示——包含 “隐含位” （个位）的尾数的位数。
- float精度(SP, single-precision)： 24 bits 有效位数（仅指尾数位）——不含符号位、指数部分.
  - 为什么书上是23位?
    
    实际上只存储了23位，但算上隐含位，数据的有效位就是24位。看语境。
- double精度(DP, double-precision)： 53 bits 有效位数（仅指尾数位）——不含符号位、指数部分.
  - 为什么书上是52位?
    
    同上。
- double extended精度(EP, extended-precision 我编的)： 64 bits
  
  注意 EP精度是没有隐含位的，所以只有SP和DP的有效位是比尾数位数多1位的。

2 IEEE754 个人整理

2.1 基本概念

计算机里存数据，有两种存法：定点数 和 浮点数。

二者特点

定点格式表示的范围有限，但硬件要求简单；浮点格式表示的范围大，但硬件要求复杂。
定点格式，即把小数点给固定了

小数点固定的位置理论上可以自定义，但一般用来表示纯整数（认为小数部分为0，i.e. $x\in Z$ ）或纯小数（认为整数部分为0，i.e. $x\in (-1,1)$ ）.

所以，定点格式可以表示“定点整数”和“定点小数”。

默认定点数指纯整数，如C语言里的 int型.
浮点格式，说白了就是用科学计数法表示浮点数

将科学计数法的三个部分抠出来分别保存：符号位、尾数位、指数位。

这个尾数部分，就是科学技术法后的浮点数部分，计算机中用“定点小数”的形式来存。

如，十进制中的 52431.66，用科学计数法表示是 $5.243166 \times 10^4$ ，则 $5.243166$ 就是尾数部分，指数部分是 $4$ ；当然，你也可以表示成 $52.43166 \times 10^3$ ，则 $52.43166$ 就是尾数部分，指数部分是 $3$ ；（后文都默认用二进制进行叙述）

C语言里的double、float都是浮点格式。

下文再细说。
思考点

定点数里的“小数”概念和浮点数概念，我总觉得有点像，如何区分？

确实挺像的。

“小数” 概念指的是真值 $∣ x ∣ < 1$ 的“数”，即只有小数点右边部分；

“定点小数” 概念指的是，用定点格式存“小数”；

“浮点数” 概念，是生活中的浮点数，如1.2325、5.1169等，既有小数点左边也有小数点右边，而在计算机中用“浮点格式”拆成三个部分（如上所说）进行存储，其中的尾数部分，采用了“定点小数”的格式进行存储。

总结，所以是套娃的概念——“浮点格式”包含了“定点数“的知识点。
什么是规格化？

见目录的【一 2.4】

2.2 IEEE754浮点基本格式

2.2.1 前言

浮点格式，“浮点”就体现在“小数点对存储数而言可以动态调整”。

IEEE格式中，规格化后的浮点数 $x$ 的表示方式如下：

$x=(-1)^S \times (1.M) \times 2^{E-127}, e=E-常数c$

其中， $S$ 是符号、 $M$ 是尾数（不存隐含位）、 $e$ 是指数、 $E$ 是阶码（即偏移后的指数）、常数 $c$ 叫指数偏移值；

在存储使用时， $S$ 用 $0∣1$ 表示、 $M$ 用原码表示（不含隐含位）、 $E$ 统一用移码表示（移码的表示规则很简单，表现出来和偏移的效果一样~）.

下文表格中，默认“指数”一词表示的是“指数位”的值，即 阶码 $E$ 的值.

2.2.2 IEEE754格式与参数

这里罗列出我总结的IEEE浮点数格式的主要参数方便查阅：

SP就是float；DP就是double；EP是x86下的双精度扩展格式。

待会儿会再细说一下这个EP，我对其是知之甚少。

整理了两个表：

图[1] IEE754浮点数常用三个类型-位宽记录
图[2] IEE754浮点数常用三个类型-范围与常用参数

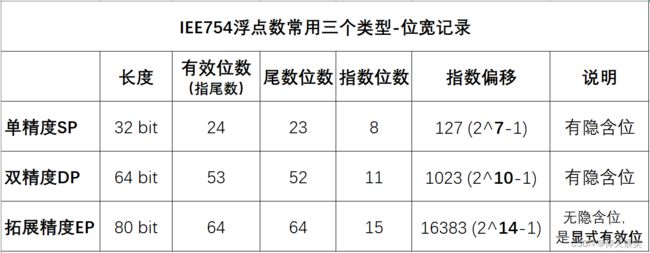
表格内有趣的一点是，表示非规格化数时，取的 $E$ 值是 $1 - bia s$ 而不是 $0 - bia s$ ，是为什么呢？

这是为了使非规格化数与规格化数表示的两个范围, 能平滑的过渡，以假设的8位浮点格式为例：

（来源于blog —— 详解浮点数的规格化表示 —— CSDN HelloAaric ）

如图所示，非规格化数的 $E$ 选用 $1 - bia s$ 而不是 $0 - bia s$ 可使得非规格化数与规格化数表示的范围能更加平滑！

2.2.3 细谈EP精度

EP是x86下的双精度扩展格式，它的格式和前面俩SP、DP有点不同——没有隐含位1，而是用显式的1来存。

在x86体系结构中，EP类型的值是连续存储在十个相连地址的 8 位字节中，其格式是这样的：

其取数范围见上图，已贴过。

2.3 IEEE754的特殊值、异常、以及舍入问题

2.3.1 特殊值

非数 NaN (Not a Number)

IEEE754的浮点数，会预留出几个表示形式，供系统用来作为signal而不是数——NaN.

触发条件： $0)^{max}$ ，符号位是被忽略的。
- 若尾数最高位为 0，则为SNAN (Signaling NAN)
- 若尾数最高位为 1，则为QNAN (Quiet NAN)，表示无效异常：如src是Inf或NaNs且VE=0.

2.3.2 异常

异常处理【处理过程略，可见西电的《浮点倒数方根》paper】
- 无效异常 (Invalid)
  
  src是NaN、平方根倒数中src是负数、 $\frac{\infty}{\infty}$ 、 $\frac{0}{0}$ 、 $\infty \cdot 0$ 、 $\infty-\infty$ .
- 除零异常 (Division by Zero)
  
  $\frac{!0}{0}$ 、平方根倒数中src是0.
- 上溢异常 (Overflow)
  
  中间结果的指数超出最大范围。
- 下溢异常 (Underflow)
  
  中间结果是一个"tiny"，若是使能信号为0，那么说明它还在传输中损失了精度！
- 不精确异常 (Inexact)
  
  可能①：舍入前后的中间结果，在精度和指数的值出现不同；（计算机二进制存储浮点数的常见情况~）
  
  可能②：上溢或下溢的使能为1，但结果的位数与中间结果的尾数不同；
  
  可能③：上溢的使能为0，但出现上溢的舍入结果。

2.3.3 舍入

中间结果与“无限精度、无限范围”的理解

IEEE754要求，在计算出结果之前，会先存储一个“无限精度、无限范围”的中间结果，经过舍入以后，才会得到最终结果。

我一度很疑惑这“无限精度、无限范围”的概念：意思是真的是”无限位数、无限精度“吗？。

网上冲浪这么久，我个人的理解是：

不是，就是一个比最终结果相对更加精确的意思而已…(￣▽￣)"
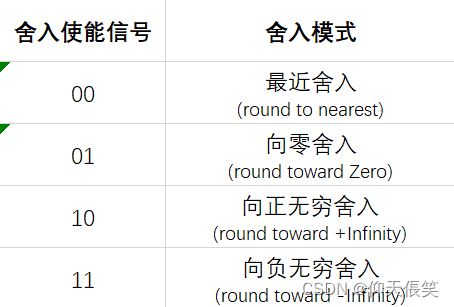
舍入模式

$Z 2 < Z < Z 1$ ，其中 $Z$ 是中间结果值、 $Z 2$ 与 $Z 1$ 是对 $Z$ 舍入后的四舍五入的两种情况。

共有四种舍入模式：

舍入的状态位
- 概括
  
  一些“舍入实现”的硬件设计上，可能会设置一些状态位来为“舍入算法”服务。这些状态位的设立目的是什么呢？来，我一起顺手把它看掉。
  fraction就是尾数的小数部分. S是符号位，C是进位，L是尾数的隐藏位. 比较不好理解的是后面三个bit位。
  在IEEE754中，在对浮点数中间结果进行无限精度计算后，在舍入时，需要存储三个bit 信息：G (guard bit), R (round bit), X (stick bit).
- 如何理解 G、R、X 这些位的作用呢？
  
  它们的作用是，舍入采用round to nearest策略时，方便进行舍入的评判：
  
  若有个中间结果的二进制尾数fraction部分在规格化后是： $x=xxx.xxx\ abcdef$ ，而最终结果需要保留到3位小数。那么根据定义， $G = a, R = b$ ，而 $X$ 的值是这么来的：若 $c, d, e, f$ 中有任何1个"1"，那么 $X = 1$ ，若 $\to X=0$ .
  - G和R是中间结果有效位后面的两位bit值，X是剩余位是否有"1"的状态证明flag。
  由于round to nearest策略的规则是：若余数小于LSB (最低有效位，the least significant bit) 的一半就舍弃、等于LSB的一半就让LSB保持odd、大于LSB的一半就进位 —— 可得到：若 $G = 0$ ，则舍弃；若 $G = 1$ 且 $R = X = 0$ 则保持odd；若 $G = 1$ 而 $R=1\ |\ X=1$ 则进位。
  
  那么很神奇的是，不论中间结果超出有效位需要被舍弃掉的位数有多长，有了 $G, R, X$ 三位flag（缺一不可）就足以实现round to nearest策略了、而不需要存储其他bit或进行其他冗杂的舍入判断了！
  
  对于更细致的理解 $G, R, X$ 在round off时的工作原理，可以见此篇文章，非常具体直观。
  
  function of Guard bit
舍入的误差描述—— $u lp$ 的概念

在网上看到一本书的截图，大概这个意思：浮点数的精度，通常可以用近似值与实际值的LSB 的所在位数来表示，这个数叫做 末位单位或最低精度，简称 ulp (unit in the last place or unit of least precision).

根据这篇博客：ulp(unit in the last place)是什么意思 —— lubxx CSDN

IEEE754中 $1\ ulp$ 的值，就是在当前浮点数 $x$ 所处的数轴中，系统能精确表示的相邻浮点数的差（当前位置IEEE754所能表达的最小精度）！根据不同的round off规则（round to 0 或者是round to nearest等四种），其误差计算的方式是：abs( x - 近似存的那个数)/ulp = 多少个ulp.

在没有发生上溢、下溢等异常情况下，IEEE754也可以保证浮点运算的精度控制在 $\frac{1}{2} ulp$ 的范围内（书上说的）。

2.4 规格化和IEEE754标准的规格化

这个概念之前一直没搞懂。

一个很重要的概念：

① 规格化 $\neq$ IEEE标准的规格化！
② 规格化的概念是对于小数的，整数没有规格化！

规格化

normalized number 规格化数；subnormal number 未规格化的数.

“是否规格化”不是主观自定义的，是确定的。就是说，“未规格化”的MSB一定是在小数点右边.

设，有纯小数 $x$ 的二进制是这样的： $[x]_? = x_n.x_{n-1}\cdots x_0$ ，其中** $x_n$ 是符号位，中间那个 $\cdot$ 是小数点，右边都是小数部分，没有隐含位**.

规格化：规定尾数的最高数位必须是1. 注：指是真值的最高数位，且 不算符号位！
- 左规：尾数左移（小数点 右移），阶码减1；
- 右规：**尾数 ** 右移（小数点 左移），阶码加1；（溢出时要处理）
  
  反应不够快，可以这么想象画面：尾数后面很多个是一队的蛋，在尺子上左右移动，而小数点是一个木桩，小数点右边有一个计数器（阶码）在随着蛋的进出加减变化，流出减少、流入增加。
因此，不同机器码规格化后效果不同：
- 原码
  
  （正数负数是对称的，好理解。）
  
  正数为： $0.1\ XX \cdots X$ .
  - 故其最大值为 $0.11 \cdots 1$ ；最小值为 $0.10 \cdots 0$ .
    
    对应真值 $1-2^{-n}\geq x \geq 2^{-1}$ .
  负数为： $1.1\ XX \cdots X$ .
  - 故其最大值为 $1.10 \cdots 0$ ；最小值为 $1.11 \cdots 1$ .
    
    对应真值 $-(2^{-1})\geq x \geq -(1-2^{-n})$ .
- 补码
  
  （正数和原码一样、没变；负数看的是真值的最高数位得是1，而不是机器码的最高位为1，所以补码的最高有效位就变成0了！另一方面，补码是原码负数部分的取反，因此补码表示的范围多1，故真值范围变化了）
  
  正数为： $0.1\ XX \cdots X$ .
  - 故其最大值为 $0.11 \cdots 1$ ；最小值为 $0.10 \cdots 0$ .
    
    对应真值 $1-2^{-n}\geq x \geq 2^{-1}$ .
  负数为： $1.0\ XX \cdots X$ .
  - 故其最大值为 $1.01 \cdots 1$ ；最小值为 $1.00 \cdots 0$ .
    
    对应真值 $-(2^{-1}+2^n)\geq x \geq -(1)$ .
IEEE754标准的规格化

IEEE754由于已经把最高有效位的那个“1”直接隐含掉了！所以根本不需要考虑 “尾数、阶码是不是要出现这个、那个的 $.01111$ 还是什么 $.111$ 还是什么 $.1000$ ” 的破情况了！

好家伙，原来是这样！

呜呜呜… 感动，终于分清楚了…

2.5 IEEE754的精度问题讨论

之前有印象，但没有例子，不够具体，于是搜了确认了一下。

IEEE754下表示的浮点数范围是变大了（和定点数比），但位数就这么多，表示的“数的个数”是有限的，那肯定导致范围内的有些数是表示不了的。

可以详细参考这篇博客，写的不错也很细：

IEEE754标准: 三, 为什么说32位浮点数的精度是"7位有效数" —— 知乎小姬

我概括、抽取下其中的重点内容：

IEEE754格式中，由于有指数位，所以尾数的变化相同次数后，指数就会 $+ 1$ ，但随着指数的增加，这个精度也是会随着指数的增加而变得粗糙——例如，最开始尾数从 $00\cdots 0$ （全0）变化到 $11 \cdots 1$ （全1），指数是从 $2^{-126}$ 上升为 $2^{-125}$ ；到后来，尾数变化的次数是相同的（位数就这么多），指数是从 $2^{126}$ 上升为 $2^{127}$ ，能表示的数值的精度间隔直接从小数点后变成整数了！

因此，IEEE754就是因此有很多数值是没法存储的，而且这个精度的间隔是在随着指数的增加而越变越大。若把IEEE754所表示的浮点数想象成一个表盘的话, 那表盘上的蓝点不是均匀分布的, 而是越来间隔越大, 越来越稀疏。

跟着这个blog，我在C语言里也做了实验，如下：

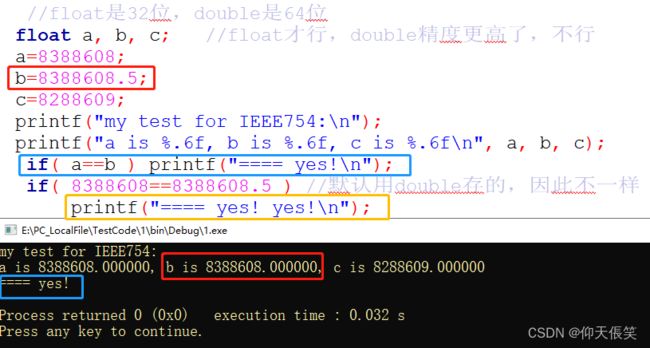
这个程序反应了32位IEEE754浮点数（C里的float型），是无法存储8388608.5这个数值的！

而以前在ACM里，常使用的浮点数比较的语句：

if( a-b< 1e-6 ) printf(...equal...);

这个 1e-6 就是来源于此。这个数值就是32位下的IEEE754 规格化范围内的浮点数的最小精度间隔！其精确值大概是： $1.19209 e - 7$ ，小于这个数，float类型就100%区分不出来啦~(￣▽￣)"…

二顺便复习四种机器码

以前对机器码的学习，最无法理解的是对应的“表示公式”在说啥？现在重新捋顺了。

其次，以前更偏向感性的学习（知道概念，但做题慢）；但对于机器码，我目前的认为最好还是理性的去学习，更能长时间并深入地掌握它的定义。

基础概念

书上会提出“真值”和“机器码”的两个概念，还是得认真理解它们的定义。

“真值”——在数学上计算时，表示的十进制的值。

“机器码/数”——在存储时，的存储数据形式。

如： $x]_原$ 是机器码， $x$ 是真值。

具体一点理解： $3]_原=111$ ， $- 3$ 是数学上的值，是真值； $111$ （含符号位）是机器码（此处是原码）。
- 首先，以下是后文中机器码的 $x$ 的格式：
  
  $x_nx_{n-1}\cdots x_2x_1x_0$ ，其中 $x_n$ 是符号位， $x_i$ 表示后面有 $i$ 个0.

1 原码

$KaTeX parse error: {equation} can be used only in display mode.$

这个公式以前就没看懂什么意思，其实表达的是数值计算过程——把有符号的二进制数转换 按 数学上的数值计算 ，最后 转换成无符号原码表示的意思！

便于理解的例子——以负数部分为例

单单一个 $x$ ，是把真值当成“含符号位”的二进制数的数学上的值。

$2^n$ 表示，把符号位看成无符号数的 $2^n$ .

$x$ 表示真值， $∣ x ∣$ 表示 $x$ 在数学上的绝对值。

举一个具体的例子： $9]_{原}=1\ 1001$ （含符号位）

$x$ 本身是个数值： $x=-9=-\ 1001B$ ；

则其原码是 $x]_原=1\ 1001$ (含符号位).

则 $∣ x ∣$ 就是 $x$ 的绝对值， $i . e .∣ x ∣ =$ 9;

因此，按照上面的公式，可以得到：

$[x]_原= 2^n-x = 16+|-9| = 16+9 = 25 = 11001B (无符号位) \\ \quad = 1\ 1001B（有符号位）=[-9]_{原}$

这样一来，就能看懂这种公式的写法了！(￣▽￣)"

2 反码

正数的反码等于整数的原码；负数的反码等于原码各位取反、符号位不变。

3 补码

正数的反码等于整数的原码；负数的补码等于反码+1、符号位不变。

有了上面的解释，我直接就贴出补码的公式了。