【论文笔记】Factorizable Graph Convolutional Networks
文章目录
-
- 1. Abstract
- 2. Method
-
- 2.1 Disentangling Step
- 2.2 Aggregation Step
- 2.3 Merging Step
- 3. 总体架构
- 4. 超参数的设置
Factorizable Graph Convolutional Networks,FactorGCN,可分解图卷积网络
1. Abstract
在许多真实的图中,节点之间的多个异质关系被混合并折叠成一条边。在社交网络的情况下,两个人可能是朋友、同事和同时生活在同一个城市,但通过单一的边连接,忽略了这种相互联系;在共同购买场景中,产品是由于促销、功能互补等不同原因一起购买的,但在图的构建中往往被忽略。在这些情况下,FactorGCN将提供一个清晰的、可解释的解决方案来解释潜在的基本原理
FactorGCN解离出的每一个子图代表一种潜在的关系,可以理解为只包含一种边类型的图。然后在每个因子分解的潜在空间中分别聚合节点的特征,生成解纠缠的特征,从而提高后续任务的性能。
在合成数据集和真实数据集上对提出的factororgcn进行了定性和定量的评价,并证明了它在分解和特征聚合方面都产生了真正令人鼓舞的结果
过去的Disentangling都在潜在特征生成阶段,尽管在 CNN Disentangling方面有许多先前的努力,但在应用图卷积网络 (GCN) 模型的不规则结构域中进行Disentangling的工作很少。 2019年的Disentangled graph convolutional networks是GNN上的首创,但是只在node-level级别进行邻居分割。
而FactorGCN进行graph-level disentangling,基于卷积特征的聚合。 对节点进行解离分割形成的子图是局部的特征聚合,而对边进行解离,是全局级别的解离,因为每一种类型的都边存在于整个拓扑图中。
图中有的边出现在多个子图中?
block-wise:对于每一节点的特征,其特征表示是分块的,其中每一块的特征是从对应的因子图中抽取出来,块内不同维度的特征相关性也比较大
-
Graph-level Disentangling.
-
Multi-relation Disentangling:多关系解缠,这意味着中心节点可以聚合来自多个关系类型的邻居的信息
-
Quantitative Evaluation Metric:
网格领域现有的定量评价方法依赖生成模型,如auto-encoder或GAN。然而在不规则区域,不幸的是,最先进的图生成模型只适用于生成小的图或没有特征的大的图。此外,这些模型包含一个连续的生成步骤,使其不可能集成到图解纠缠框架中。为此,我们提出了一个基于图编辑距离的度量,它绕过生成步骤,估计因子图与地面真实之间的相似性。
2. Method
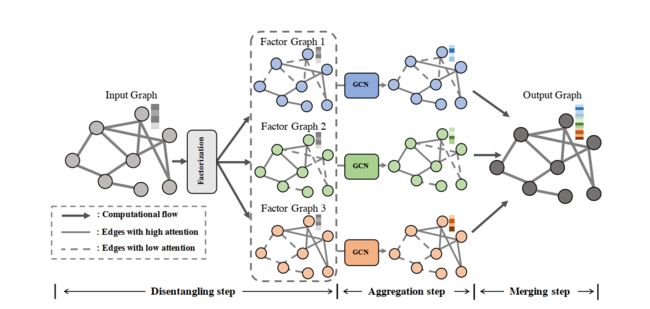
2.1 Disentangling Step
鉴别器被认为是一个三层 GCN,然后是一层 MLP。 输入鉴别器是维数为 F 的节点的变换特征和因子图。 这三层 GCN 的隐藏特征的维度分别设置为 F、F/2 和 F。非线性激活函数是 Tanh,没有使用残差连接。 那么平均池化是应用于生成的节点特征以获得图的特征。 然后将这些特征输入到为每个类生成激活的一层 MLP
输入的大图记为 h = { h 0 , h 1 , … , h n } , h i ∈ R F \mathbf{h}=\left\{h_{0}, h_{1}, \ldots, h_{n}\right\}, h_{i} \in \mathcal{R}^{F} h={h0,h1,…,hn},hi∈RF, e = { e 0 , e 1 , … , e m } , e k = ( h i , h j ) \mathbf{e}=\left\{e_{0}, e_{1}, \ldots, e_{m}\right\}, e_{k}=\left(h_{i}, h_{j}\right) e={e0,e1,…,em},ek=(hi,hj), h h h是点集, e e e是边集。
变换后的特征被用来生成因子系数如下:
E i j e = 1 / ( 1 + e − Ψ e ( h i ′ , h j ′ ) ) ; h ′ = W h (1) E_{i j e}=1 /\left(1+e^{-\Psi_{e}\left(h_{i}^{\prime}, h_{j}^{\prime}\right)}\right) ; h^{\prime}=\mathbf{W} h \tag{1} Eije=1/(1+e−Ψe(hi′,hj′));h′=Wh(1)
函数 Ψ e \Psi_{e} Ψe以节点i和节点j的特征为输入,来计算子图e的边的注意力分数(实现时,采用单层MLP的形式)。
E i j e E_{i j e} Eije将注意力分数归一化为[0,1],代表子图 e e e中从节点 i i i到节点 j j j的边的系。 h ′ h^{\prime} h′是转换后的节点特性,在所有 Ψ e \Psi_{e} Ψe函数中共享。
与以往大多数基于注意力的GCNs形式不同,我们提出的模型直接生成这些系数作为子图(generates these coefficients directly as the factor graph.)
一旦计算出所有的系数,某一个子图 e e e就可以用 E e E_e Ee来表示,它将用于下一个聚合步骤。
然而,在没有其他约束的情况下,生成的一些因子图可能包含类似的结构,降低了模型的解纠缠性能和能力。因此, 在the disentangle layer中加入一个多余的head ,目的是避免生成的因子图的退化
附加head的动机是:
一个disentangled好的子图应该有足够的信息,仅根据其结构就可以与其他的区分开来。但实际上,直接区分是难以实现的,所以 additional head相当于给子图一个唯一的标签,把子图作为一个图分类问题来求解。
我们把additional head称为discriminator(鉴别器):
G e = Softmax ( f ( Readout ( A ( E e , h ′ ) ) ) ) (2) G_{e}=\operatorname{Softmax}\left(f\left(\operatorname{Readout}\left(\mathcal{A}\left(\mathbf{E}_{e}, \mathbf{h}^{\prime}\right)\right)\right)\right) \tag{2} Ge=Softmax(f(Readout(A(Ee,h′))))(2)
-
包含一个三层图自编码器 A \mathcal{A} A,以 h ′ h^{\prime} h′和子图 E e E_e Ee生成的注意系数为输入,生成新的节点特征
-
Readout读出这些特征以生成整个子图的表示。
在进行图分类的最后一个步骤一般需要一个读出(readout)函数,读出函数的作用是聚合所有的节点获得一个graph-level的表示,用于分类回归等任务。
-
特征向量将被发送到一个全连接层的分类器。
注意,所有的子图分享相同的节点特征,确保这个鉴别器挖掘的信息是来自于子图结构的不同而不是因为节点的表示不同
训练鉴别器的损失函数是:
L d = − 1 N ∑ i N ( ∑ c = 1 N e 1 e = c log ( G i e [ c ] ) ) (3) \mathcal{L}_{d}=-\frac{1}{N} \sum_{i}^{N}\left(\sum_{c=1}^{N_{e}} \mathbb{1}_{e=c} \log \left(G_{i}^{e}[c]\right)\right) \tag{3} Ld=−N1i∑N(c=1∑Ne1e=clog(Gie[c]))(3)
- N N N为训练样本个数,设为输入图个数乘因子图个数(类别数)( k × k k\times k k×k)
- N e N_e Ne为子图种类数(the number of factor graphs)
- G i e G_i^e Gie是样本 i i i的分布, G i e [ c ] G_i^e[c] Gie[c]表示生成的子图有标签c的概率
- 1 e = c \mathbb{1}_{e=c} 1e=c是一个指标函数,当预测的标签正确时取为1。
2.2 Aggregation Step
唯一的不同,每个子图的聚合都是独立发生的
h i ( l + 1 ) e = σ ( ∑ j ∈ N i E i j e / c i j h j ( l ) W ( l ) ) , c i j = ( ∣ N i ∣ ∣ N j ∣ ) 1 / 2 (4) h_{i}^{(l+1) e}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} E_{i j e} / c_{i j} h_{j}^{(l)} \mathbf{W}^{(l)}\right), c_{i j}=\left(\left|\mathcal{N}_{i}\right|\left|\mathcal{N}_{j}\right|\right)^{1 / 2} \tag{4} hi(l+1)e=σ⎝⎛j∈Ni∑Eije/cijhj(l)W(l)⎠⎞,cij=(∣Ni∣∣Nj∣)1/2(4)
$ E_{i j e} 就 是 子 图 就是子图 就是子图e 中 边 中边 中边ij 的 权 重 系 数 , 的权重系数, 的权重系数,c_{ij} 是 根 据 节 点 I 和 节 点 j 的 度 计 算 的 归 一 化 项 , 是根据节点I和节点j的度计算的归一化项, 是根据节点I和节点j的度计算的归一化项,W$和Disentangling Step使用的是同一矩阵(注意,尽管我们使用输入图中节点的所有邻居来聚合信息,但如果因子图中相应的系数为零,其中一些邻居就没有贡献)
2.3 Merging Step
h i ( l + 1 ) = ∥ e = 1 N e h i ( l + 1 ) e h_{i}^{(l+1)}=\|_{e=1}^{N_{e}} h_{i}^{(l+1) e} hi(l+1)=∥e=1Nehi(l+1)e
N e N_{e} Ne是子图的个数
3. 总体架构
上面三个步骤组成一个disentangle layer,在实验部分的FactorGCN模型包含了几个disentangle layer,增加了表达能力。此外,该模型通过在不同层中设置不同数量的子图,可以分层分解输入数据。
FactorGCN模型的总 l o s s loss loss为 L = L t + λ ∗ L d \mathcal{L}=\mathcal{L}_{t}+\lambda * \mathcal{L}_{d} L=Lt+λ∗Ld。 L t \mathcal{L}_{t} Lt是原始任务的损失, L d \mathcal{L}_{d} Ld是上面提到的鉴别器的损失, λ \lambda λ是平衡这两种损失的权重。
在这里,我们使用六个数据集来评估所提出方法的有效性。 第一个是包含固定数量的预定义图作为因子图的合成数据集。 第二个是由分子图构建的 ZINC 数据集 [Dwivedi et al., 2020]。 第三个是模式数据集[Dwivedi et al., 2020],这是一个用于节点分类任务的大规模数据集。 其他三个被广泛使用的图分类数据集包括**社交网络(COLLAB,IMDB-B)**和生物信息学图(MUTAG)[Yanardag 和 Vishwanathan,2015]。 为了生成包含 Ne 因子图的合成数据集,我们首先生成 Ne 预定义图,它们是众所周知的图,如 Turán 图、house-x 图和平衡树图。 然后我们选择其中的一半并用孤立的节点填充它们,使节点数为 15。填充后的图将合并在一起作为训练样本。 合成数据的标签是一个二元向量,维度为 Ne。 根据样本生成的图形类型,一半的标签将设置为 1,其余的设置为零。 有关数据集的更多信息可以在补充材料中找到
4. 超参数的设置
当因子图个数不大于4时,隐藏特征的维数设置为32,不大于64。将factororgcn中鉴别器损耗的权重设置为0.5