Python应用实例（二）数据可视化（二）

1.随机漫步

使用Python来生成随机漫步数据，再使用Matplotlib以引人瞩目的方式将这些数据呈现出来。随机漫步是这样行走得到的路径：每次行走都是完全随机的、没有明确的方向，结果是由一系列随机决策决定的。你可以将随机漫步看作蚂蚁在晕头转向的情况下，每次都沿随机的方向前行所经过的路径。

在自然界、物理学、生物学、化学和经济领域，随机漫步都有其实际用途。例如，漂浮在水滴上的花粉因不断受到水分子的挤压而在水面上移动。水滴中的分子运动是随机的，因此花粉在水面上的运动路径犹如随机漫步。我们稍后编写的代码将模拟现实世界的很多情形。

1.1 创建RandomWalk类

为模拟随机漫步，将创建一个名为RandomWalk的类，它随机地选择前进方向。这个类需要三个属性：一个是存储随机漫步次数的变量，其他两个是列表，分别存储随机漫步经过的每个点的x坐标和y坐标。

RandomWalk类只包含两个方法：方法__init___()和fill_walk()，后者计算随机漫步经过的所有点。先来看看__init__()，如下所示：

random_walk.py

❶ from random import choice

  class RandomWalk:
      """一个生成随机漫步数据的类。"""

❷     def __init__(self, num_points=5000):
          """初始化随机漫步的属性。"""
          self.num_points = num_points

          #所有随机漫步都始于(0, 0)。
❸         self.x_values = [0]
          self.y_values = [0]

为做出随机决策，将所有可能的选择都存储在一个列表中，并在每次决策时都使用模块random中的choice()来决定使用哪种选择（见❶）。接下来，将随机漫步包含的默认点数设置为5000。这个数大到足以生成有趣的模式，又小到可确保能够快速地模拟随机漫步（见❷）。然后，在❸处创建两个用于存储[插图]值和[插图]值的列表，并让每次漫步都从点(0, 0)出发。

1.2 选择方向

我们将使用方法fill_walk()来生成漫步包含的点并决定每次漫步的方向，如下所示。请将这个方法添加到random_walk.py中：random_walk.py

      def fill_walk(self):
          """计算随机漫步包含的所有点。"""

          # 不断漫步，直到列表达到指定的长度。
❶         while len(self.x_values) < self.num_points:

              # 决定前进方向以及沿这个方向前进的距离。
❷             x_direction = choice([1, -1])

              x_distance = choice([0, 1, 2, 3, 4])
❸             x_step = x_direction * x_distance

              y_direction = choice([1, -1])
              y_distance = choice([0, 1, 2, 3, 4])
❹             y_step = y_direction * y_distance

              # 拒绝原地踏步。
❺             if x_step == 0 and y_step == 0:
                  continue

              # 计算下一个点的x值和y值。
❻             x = self.x_values[-1] + x_step
              y = self.y_values[-1] + y_step

              self.x_values.append(x)
              self.y_values.append(y)

❶处建立了一个循环，它不断运行，直到漫步包含所需的点数。方法fill_walk()的主要部分告诉Python如何模拟四种漫步决定：向右走还是向左走？沿指定的方向走多远？向上走还是向下走？沿选定的方向走多远？

使用choice([1, -1])给x_direction选择一个值，结果要么是表示向右走的1，要么是表示向左走的-1（见❷）。接下来，choice([0, 1, 2, 3, 4])随机地选择一个0～4的整数，告诉Python 沿指定的方向走多远（x_distance）。通过包含0，不仅能够同时沿两个轴移动，还能够只沿一个轴移动。

在❸和❹处，将移动方向乘以移动距离，确定沿[插图]轴和[插图]轴移动的距离。如果x_step为正将向右移动，为负将向左移动，为零将垂直移动；如果y_step为正将向上移动，为负将向下移动，为零将水平移动。如果x_step和y_step都为零，则意味着原地踏步。我们拒绝这样的情况，接着执行下一次循环（见❺）。

为获取漫步中下一个点的[插图]值，将x_step与x_values中的最后一个值相加（见❻），对[插图]值也做相同的处理。获得下一个点的[插图]值和[插图]值后，将它们分别附加到列表x_values和y_values的末尾。

1.3 绘制随机漫步图

下面的代码将随机漫步的所有点都绘制出来：rw_visual.py

  import matplotlib.pyplot as plt

  from random_walk import RandomWalk

  # 创建一个RandomWalk实例。
❶ rw = RandomWalk()
  rw.fill_walk()
  # 将所有的点都绘制出来。
  plt.style.use('classic')
  fig, ax = plt.subplots()
❷ ax.scatter(rw.x_values, rw.y_values, s=15)
  plt.show()

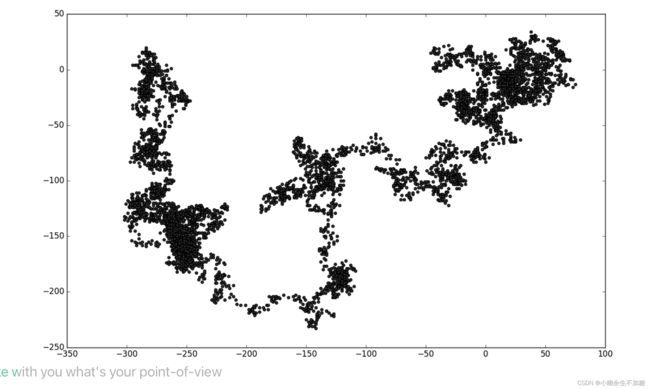
首先导入模块pyplot和RandomWalk类，再创建一个RandomWalk实例并将其存储到rw中（见❶），并且调用fill_walk()。在❷处，将随机漫步包含的[插图]值和[插图]值传递给scatter()，并选择合适的点尺寸。图15-9显示了包含5000个点的随机漫步图。（本节的示意图未包含Matplotlib查看器的界面，但你运行rw_visual.py时会看到。）

1.4 模拟多次随机漫步

每次随机漫步都不同，因此探索可能生成的各种模式很有趣。要在不多次运行程序的情况下使用前面的代码模拟多次随机漫步，一种办法是将这些代码放在一个while循环中，如下所示：rw_visual.py

import matplotlib.pyplot as plt

from random_walk import RandomWalk

# 只要程序处于活动状态，就不断地模拟随机漫步。
while True:
    # 创建一个RandomWalk实例。
    rw = RandomWalk()
    rw.fill_walk()

    # 将所有的点都绘制出来。
    plt.style.use('classic')
    fig, ax = plt.subplots()
    ax.scatter(rw.x_values, rw.y_values, s=15)
    plt.show()

    keep_running = input("Make another walk? (y/n): ")
    if keep_running == 'n':
        break

这些代码模拟一次随机漫步，在Matplotlib查看器中显示结果，再在不关闭查看器的情况下暂停。如果关闭查看器，程序将询问是否要再模拟一次随机漫步。如果输入y，可模拟在起点附近进行的随机漫步、大多沿特定方向偏离起点的随机漫步、漫步点分布不均匀的随机漫步，等等。要结束程序，请输入n。

1.5 设置随机漫步图的样式

本节将定制图表，以突出每次漫步的重要特征，并让分散注意力的元素不那么显眼。为此，我们确定要突出的元素，如漫步的起点、终点和经过的路径。接下来确定要使其不那么显眼的元素，如刻度标记和标签。最终的结果是简单的可视化表示，清楚地指出了每次漫步经过的路径。

给点着色

我们将使用颜色映射来指出漫步中各点的先后顺序，并删除每个点的黑色轮廓，让其颜色更为明显。为根据漫步中各点的先后顺序来着色，传递参数c，并将其设置为一个列表，其中包含各点的先后顺序。这些点是按顺序绘制的，因此给参数c指定的列表只需包含数0～4999，如下所示：rw_visual.py

  --snip--
  while True:
      # 创建一个RandomWalk实例。
      rw = RandomWalk()
      rw.fill_walk()

      # 将所有的点都绘制出来。
      plt.style.use('classic')
      fig, ax = plt.subplots()
❶     point_numbers = range(rw.num_points)
      ax.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues,
          edgecolors='none', s=15)
      plt.show()

      keep_running = input("Make another walk? (y/n): ")
      --snip--

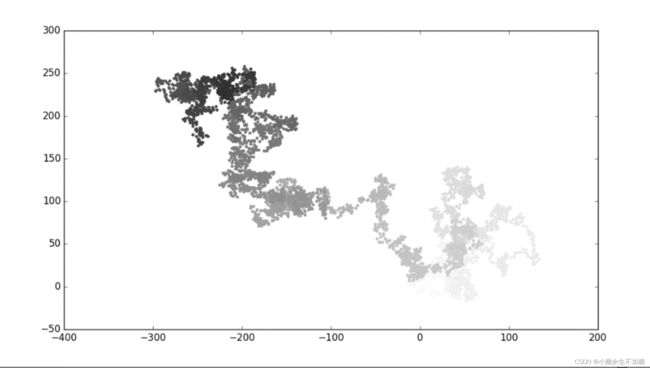
在❶处，使用range()生成了一个数字列表，其中包含的数与漫步包含的点数量相同。接下来，将这个列表存储在point_numbers中，以便后面使用它来设置每个漫步点的颜色。将参数c设置为point_numbers，指定使用颜色映射Blues，并传递实参edgecolors='none’以删除每个点周围的轮廓。最终的随机漫步图从浅蓝色渐变为深蓝色，如图所示。