Python 最优传输工具箱(Python Optimal Transport)
最近在研究最优传输的相关理论,博主使用的是python编程语言,在这里给大家推荐一个Python最优传输工具箱:Python Optimal Transport(pot)与geomloss
其中geomloss是针对pytorch张量的,ot是针对numpy数组的;geomloss支持GPU,ot仅支持cpu,但ot更为加轻量级
POT工具箱安装
使用pip安装方式
pip install POT
或者使用git安装
pip install -U https://github.com/PythonOT/POT/archive/master.zip # with --user for user install (no root)
使用conda安装方式,博主使用的便是这种安装方式
conda install -c conda-forge pot
或许还需要一些其他依赖:
pip install pymanopt autograd
geomloss工具箱安装
pip install geomloss
工具箱使用
安装这个工具箱的意义在于方便我们将数据输入后给出最优传输结果,其实主要是用Sinkhorn算法。
前面已经讲过Sinkhorn算法的原理了,这里我们直接使用即可。
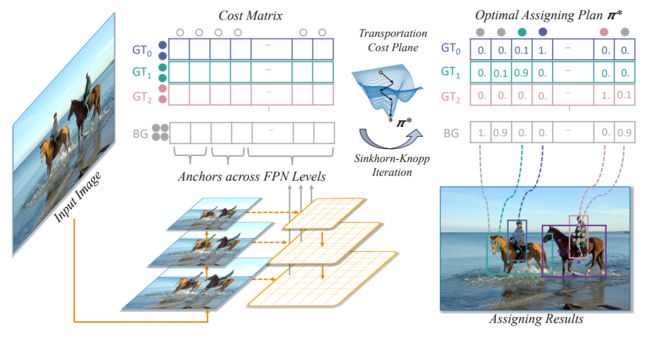
模拟目标检测中的最优传输过程,alpha为预测框,全1代表每个预测框只需要一个真值与其对应,beta代表真值框,里面的数字代表所需预测框的个数。
alpha = np.array([1, 1, 1, 1, 1, 1, 1, 1])
beta = np.array([2, 1, 1, 3, 1])
M = np.array(
[[2, 2, 1, 0, 0],
[0, -2, -2, -2, -2],
[1, 2, 2, 2, -1],
[2, 1, 0, 1, -1],
[0.5, 2, 2, 1, 0],
[0, 1, 1, 1, -1],
[-2, 2, 2, 1, 1],
[2, 1, 2, 1, -1]],
dtype=float)
使用Sinkborn算法,一般是求其传输计划P与传输距离W,这里传输计划P可以认为是具体分配,传输距离则可认为是总损失。
从OTA(Optimal Transport Assignment for Object Detection)中的描述图来看,其最终的传输计划并不是一个整数值,其求的是最后的传输距离。
那么我们该如何求Wasserstein距离与最优传输计划呢?
在ot中已经给我们封装好了该算法的实现。
首先是Wasserstein距离的计算。
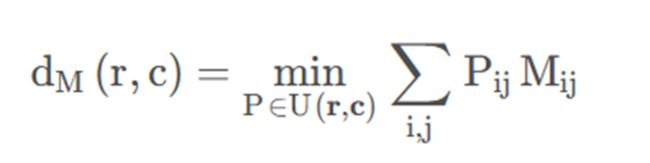
这是最原始的Wasserstein距离计算公式,其所求距离值又称EMD(Earth Mover Distance)
其可以通过调用ot.emd2这个方法来实现
pW = ot.emd2(alpha, beta, M)
求得值为:-3.0
或者通过Sinkhorn算法来实现,原本的目标函数作为一个线性规划问题,计算量太大,且解不唯一,因此有人提出可以添加正则项,通过熵的方法求近似解。
# Sinkhorn近似解
entreg = .5 # regularization term >0
P = ot.sinkhorn(alpha, beta, M, reg=entreg, numItermax=800, method='sinkhorn')
pW=P*M
print(pW.sum())
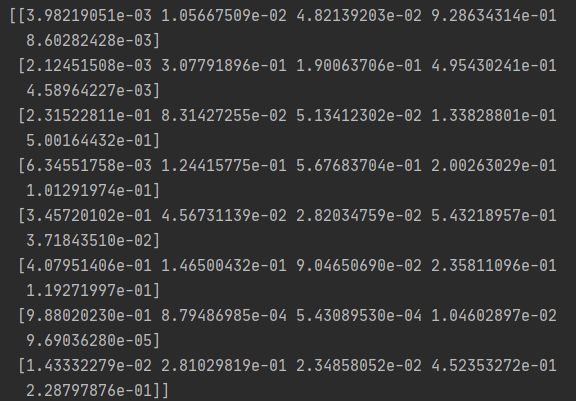
求出P为传输计划,又称关联矩阵,其值为:
而原式是要将传输矩阵与代价矩阵对应值相乘后相加,则通过pW.sum()求得。
求得值为:-1.5794554527859845
当然也可以直接通过ot中封装的方法直接求出Wasserstein距离:
pW = ot.sinkhorn2(alpha, beta, M, reg=entreg, numItermax=800, method='sinkhorn')
print("PW",pW)
求得值也为:-1.5794554527859845
由上面的计算过程可以知道,通过Sinkhorn算法求得的距离的确是一个近似解。
参考:https://zhuanlan.zhihu.com/p/573158960