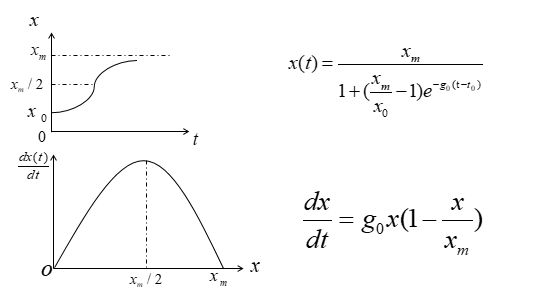
数学建模——微分方程、差分方程、数理统计
一.微分方程
- 常微分方程
【1】一元二次
% ConDiffa.m
d2y/dt2=1+dy/dt
y(0)=1,dy(0)/dt=0
clc,clear
syms y(t)
Dy = diff(y);
eqn = diff(y,t,2) == 1+diff(y,t);
cond1 = y(0) == 1;
cond2 = Dy(0) == 0;
conds = [cond1 cond2];
y = dsolve(eqn,conds)
y =
exp(t) - t【2】二元
% ConDiffb.m
dx/dt=y+x,dy/dt=2*x
x(0)=0,y(0)=1
clc,clear
syms x(t) y(t)
eqn1 = diff(x,t) == y+x;
eqn2 = diff(y,t) == 2*x;
cond1 = x(0) == 0;
cond2 = y(0) == 1;
eqn = [eqn1,eqn2];
cond = [cond1,cond2];
[x,y] = dsolve(eqn,cond)
x =
exp(2*t)/3 - exp(-t)/3
y =
(2*exp(-t))/3 + exp(2*t)/3【3】矩阵
% ConDiffc.m
[x1'] [1 0 0] [x1] [ 0 ]
[x2']= [2 1 -2] * [x2] + [ 0 ]
[x3'] [3 2 1] [x3] [exp(t)*cos(2t)]
[x1(0)] [0]
[x2(0)] = [1]
[x3(0)] [1]
clc,clear
syms x(t) [3,1]
A=[1,0,0;2,1,-2;3,2,1];
B=[0;0;exp(t)*cos(2*t)];
x0=[0;1;1];
eq=diff(x)==A*x+B;
con=x(0)==x0;
[x1,x2,x3]=dsolve(eq,con)
x1 =
0
x2 =
- sin(2*t)*exp(t)*(t/2 + sin(4*t)/8 + 1) - cos(2*t)*exp(t)*(cos(4*t)/8 - 9/8)
x3 =
cos(2*t)*exp(t)*(t/2 + sin(4*t)/8 + 1) - sin(2*t)*exp(t)*(cos(4*t)/8 - 9/8)【4】方程组
% ConDiffd.m
f''+g=3,f'+g'=1
f'(1)=0,f(0)=0,g(0)=0
clc,clear
syms f(x) g(x)
df=diff(f);
eq1=diff(f,x,2)+g==3;
eq2=diff(f,x)+diff(g,x)==1;
con1=df(1)==0;
con2=f(0)==0;
con3=g(0)==0;
eq=[eq1,eq2];
con=[con2,con2,con3];
[fx,gx]=dsolve(eq,con)
fx =
x - exp(-x)*(C1 + 2*exp(x)) + exp(x)*(C1 - exp(-x) + 3)
gx =
exp(-x)*(C1 + 2*exp(x)) - exp(x)*(C1 - exp(-x) + 3)【5】ode45
% ConDiffe.m
%ode45(y,xspan,y0)
clc,clear,close all
syms y(x)
eq=diff(y)==-2*y+2*x^2+2*x;
con=y(0)==1;
y=dsolve(eq,con)
dy=@(x,y)-2*y+2*x^2+2*x;
[sx,sy]=ode45(dy,[0,0.5],1)
fplot(y,[0,0.5]),hold on
plot(sx,sy,'*');legend({'符号解','数值解'})
xlabel('$x$','Interpreter','latex')
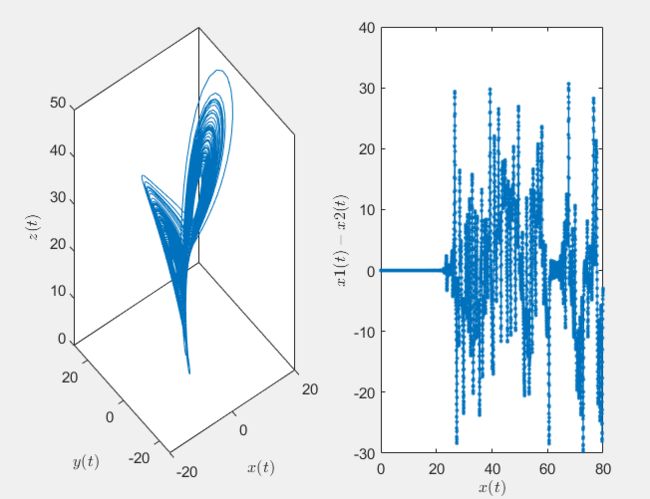
ylabel('$y$','Interpreter','latex','Rotation',0)【6】Lorenz蝴蝶效应
% ConDifff.m
clc,clear,close all,rng(2)
sigma=10;rho=28;beta=8/3;T=80;
g=@(t,f)[sigma*(f(2)-f(1));rho*f(1)-f(2)-f(1)*f(3);f(1)*f(2)-beta*f(3)];
xyz0=rand(3,1);
[t,xyz]=ode45(g,[0,T],xyz0);
subplot(121),plot3(xyz(:,1),xyz(:,2),xyz(:,3))
xlabel('$x(t)$','Interpreter','latex')
ylabel('$y(t)$','Interpreter','latex')
zlabel('$z(t)$','Interpreter','latex'),box on
so=ode45(g,[0,T],xyz0+0.00001);
xyz2=deval(so,t);
subplot(122),plot(t,xyz(:,1)-xyz2(1,:)','.-')
xlabel('$x(t)$','Interpreter','latex')
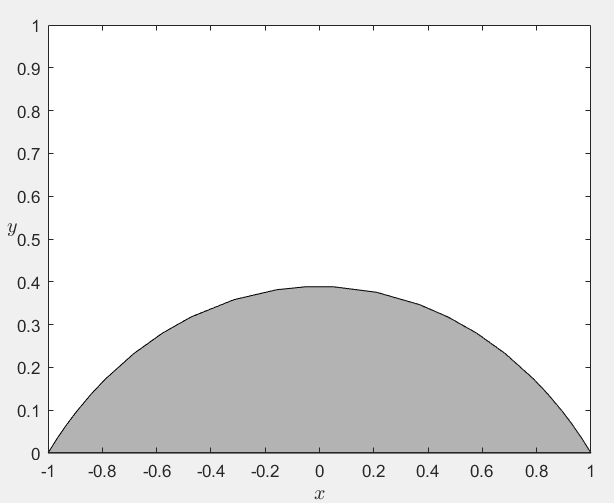
ylabel('$x1(t)-x2(t)$','Interpreter','latex')【7】边值问题
% ConDiffg.m
clc,clear,close all
solinit=bvpinit(linspace(-1,1,20),@dropinit);
sol=bvp4c(@drop,@dropbc,solinit)
fill(sol.x,sol.y(1,:),[0.7,0.7,0.7]),axis([-1,1,0,1])
xlabel('$x$','Interpreter','latex','FontSize',12)
ylabel('$y$','Interpreter','latex','Rotation',0,'FontSize',12)
function yprime=drop(x,y);
yprime=[y(2),(y(1)-1)*(1+y(2)^2)^(3/2)];
end
function res=dropbc(ya,yb);
res=[ya(1);yb(1)];
end
function yinit=dropinit(x);
yinit=[sqrt(1-x.^2);-x./(0.1+sqrt(1-x.^2))];
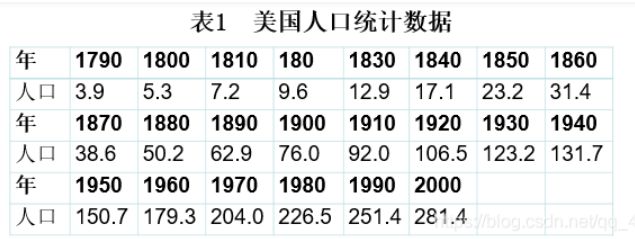
end- 案例:美国人口
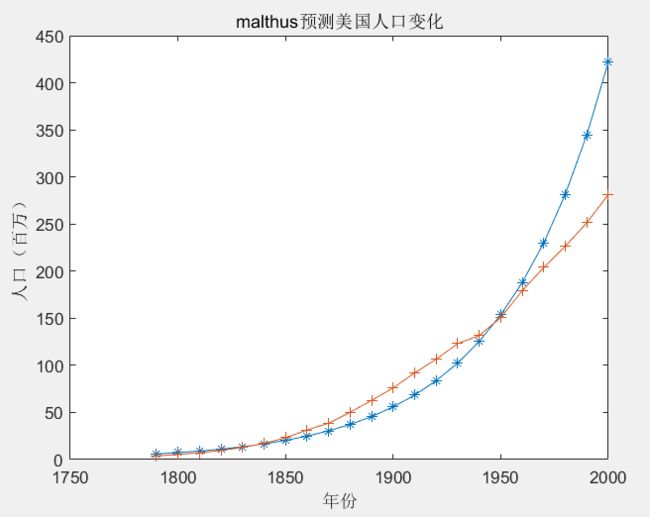
【1】malthlus模型
适用于短期的人口预测,指数型,与实际不符
% Diff_Malthlus.m
clc,clear
t=[1790:10:2000]';
a=readmatrix('Diff_Logistic.txt');
%把原始数据保存在data1.xlsx中,读取data1里保存的数据,6*8矩阵
x=a([2:2:6],:)';
%提出人口数据,提取2,4,6行(人口)数据,并且转置
x=nonzeros(x);
x=x(~isnan(x))
y=log(x); %令y=lnx
p=polyfit(t,y,1) %拟合lnx=a*t+b
g=p(1) %p(1)代表g:人口自然增长率
x0=exp(p(2))
%因为e^(a*t)*e^b=x,而x=x0*e^g*t,所以x0=e^b
Y=polyval(p,t);
%y=polyval(p,t)为返回对应自变量t在给定系数P的多项式的值。此时值为lnx
X=exp(Y); %还原成预测的x
plot(t,X,'*-',t,x,'+-')
title('malthus预测美国人口变化')
xlabel('年份')
ylabel('人口(百万)')
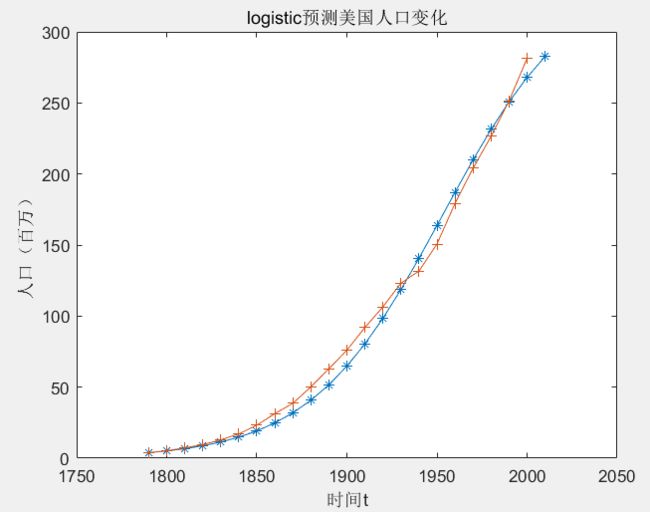
【2】logistic模型
% Diff_Malthlus.m
clc, clear
a=readmatrix('Diff_Logistic.txt');
%把原始数据保存在data1.xlsx中,读取data1里保存的数据,6*8矩阵
x=a([2:2:6],:)';
%提出人口数据,提取2,4,6行(人口)数据,并且转置
x=nonzeros(x); %去0
x=x(~isnan(x))
t=[1790:10:2000]';
t0=t(1); x0=x(1);
%取1970年的人口和年份作为初始数据
fun=@(cs,td)cs(1)./(1+(cs(1)/x0-1)*exp(-cs(2)*(td-t0))); %cs(1)=xm,cs(2)=r
cs=lsqcurvefit(fun,rand(2,1),t(2:end),x(2:end),zeros(2,1)) %非线性最小二乘估计得出cs
xhat=fun(cs,[t;2010]) %预测已知年代和2010年的人口
t1=[t;2010];
plot(t1,xhat,'*-',t,x,'+-')
title('logistic预测美国人口变化')
xlabel('时间t')
ylabel('人口(百万)')
xhat =
3.9000
5.1086
6.6844
8.7336
11.3898
14.8180
19.2180
24.8256
31.9079
40.7514
51.6384
64.8090
80.4101
98.4351
118.6708
140.6681
163.7589
187.1249
209.9081
231.3336
250.8073
267.9666
282.67813.传染病模型
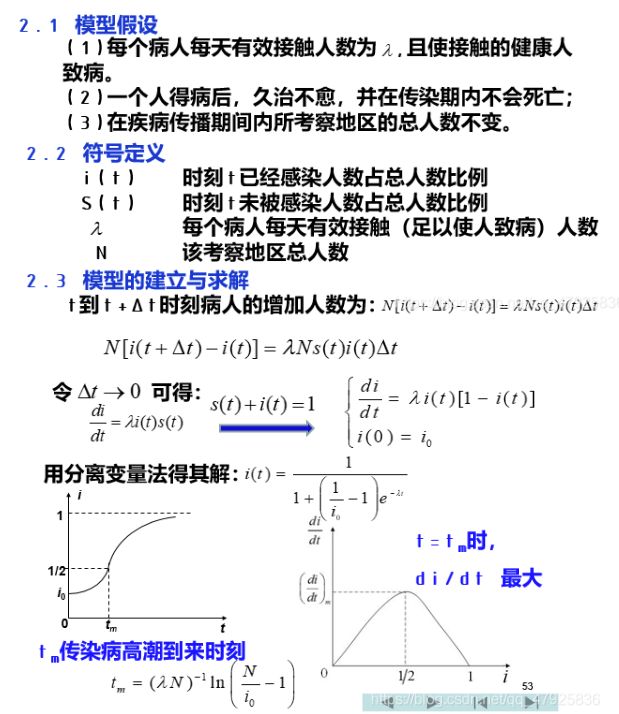
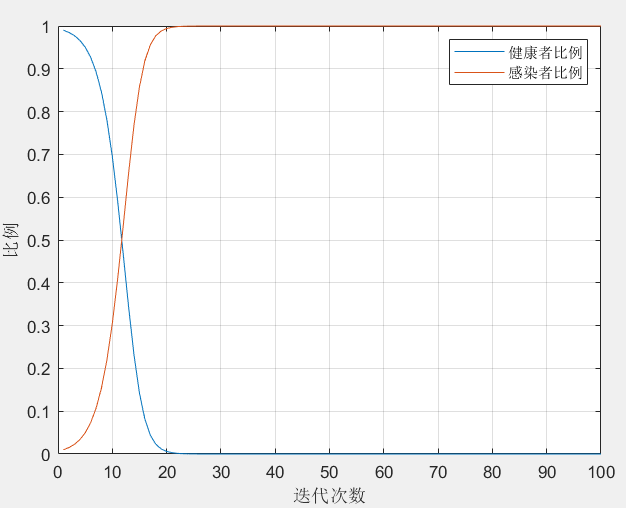
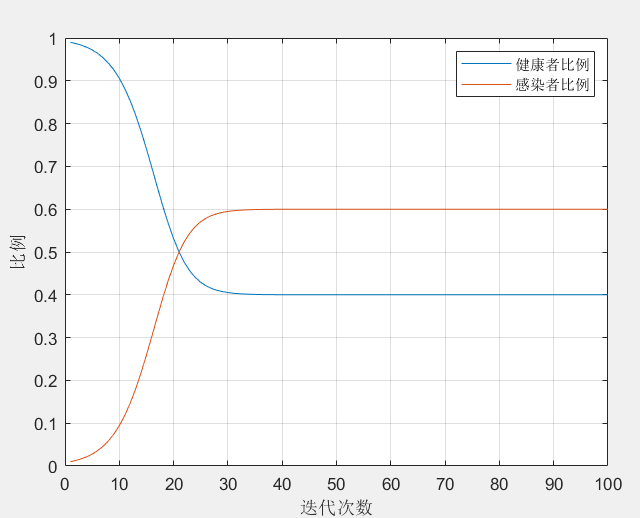
【1】SI模型
(区分病人和健康人,病人不会再被感染)
% Diff_SI.m
clear;clc;
% 定义迭代次数
n = 100;
% 定义并初始化状态E(s,i)
E = zeros(2,n);
E(1,1) = 0.99; % 初始健康者比例
E(2,1) = 0.01; % 初始感染者比例
% 初始化参数
L = 0.5; % 病人日接触率
% 开始迭代
for t = 1:n-1
E(2,t+1) = E(2,t) + L*E(2,t)*(1-E(2,t));
E(1,t+1) = 1 - E(2,t+1);
end
% 绘图
s = E(1,:); % 健康者比例数据
i = E(2,:); % 感染者比例数据
plot(s,'DisplayName','s');hold on;
plot(i,'DisplayName','i');
legend('健康者比例','感染者比例');
xlabel('迭代次数');
ylabel('比例');
grid on;
hold off;【2】SIS模型
(病人可治愈成为健康人,健康人可再次被感染)
增加每天可治愈病人u人
% Diff_SIS.m
clear;clc;
% 定义迭代次数
n = 100;
% 定义并初始化状态E(s,i)
E = zeros(2,n);
E(1,1) = 0.99; % 初始健康者比例
E(2,1) = 0.01; % 初始感染者比例
% 初始化参数
L = 0.5; % 病人日接触率
M = 0.2; % 病人日治愈率
% 开始迭代
for t = 1:n-1
E(2,t+1) = E(2,t) + L*E(2,t)*(1-E(2,t))-M*E(2,t);
E(1,t+1) = 1 - E(2,t+1);
end
% 绘图
s = E(1,:); % 健康者比例数据
i = E(2,:); % 感染者比例数据
plot(s,'DisplayName','s');hold on;
plot(i,'DisplayName','i');
legend('健康者比例','感染者比例');
xlabel('迭代次数');
ylabel('比例');
grid on;
hold off;
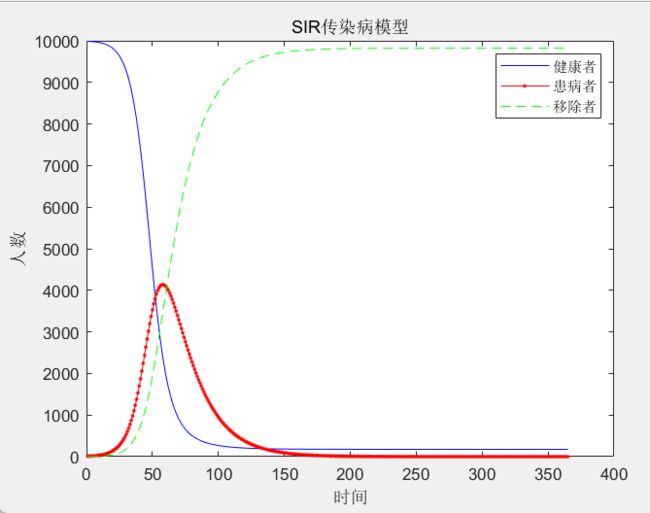
【3】SIR模型
病人被治愈后,会产生抗体,成为免疫者,免疫者群体不会被再次感染
SIR模型中,有三种人群:健康者(S),感染者(I),免疫者(R)
感染者接触健康者,就会让健康者患病
% Diff_SIR.m
clc;clear
I=input('请输入感染者的人数:');
R=input('请输入移除者的人数:');
N=input('请输入总人数:');
S=N-I-R; %健康者的人数
lemda=input('请输入日接触率:');
mu=input('请输入移除率:');
t=1:365;
for i=1:(size(t,2)-1)
S(1+i)=S(i)-lemda*I(i)*S(i)/N;
%下一时刻健康的人数等于上一时刻健康的人数减去新感染的人数
I(1+i)=I(i)+I(i)*S(i)*lemda/N-mu*I(i);
%下一时刻的病人数目等于上一时刻病人数目加上新患者人数减去移除者的人数
R(1+i)=N-I(1+i)-S(1+i);
%下一时刻移除者的数目等于总人数减去前两者的数目
end
plot(t,S,'b-',t,I,'r.-',t,R,'g--')
xlabel('时间')
ylabel('人数')
legend('健康者','患病者','移除者')
title('SIR传染病模型')
请输入感染者的人数:10
请输入移除者的人数:0
请输入总人数:10000
请输入日接触率:0.2
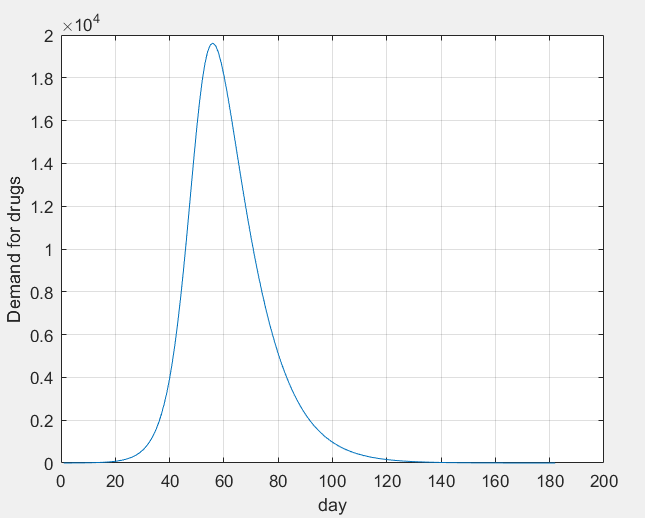
请输入移除率:0.05【4】SEIR模型
(人被感染传染病后要经历病毒潜伏期)
% Diff_SIER.m
clear;clc;
N = 29000; %人口总数
E = 0; %潜伏者
I = 1; %传染者
S = N - I; %易感者
R = 0; %康复者
m=1;
r = 25;
%感染者接触易感者的人数
B = 0.03;
%传染概率
a = 0.1;
%潜伏者转化为感染者概率
r2 = 3;
%潜伏者接触易感者的人数
B2 = 0.03;
%潜伏者传染正常人的概率
y = 0.1;
%康复概率
T = 1:182;
for idx = 1:length(T)-1
S(idx+1) = S(idx) - r*B*S(idx)*I(idx)/N(1) - r2*B2*S(idx)*E(idx)/N;
E(idx+1) = E(idx) + r*B*S(idx)*I(idx)/N(1)-a*E(idx) + r2*B2*S(idx)*E(idx)/N;
I(idx+1) = I(idx) + a*E(idx) - y*I(idx);
R(idx+1) = R(idx) + y*I(idx);
m(idx+1) = E(idx+1) + I(idx+1);
end
x=1:182;
plot(x,m);grid on;
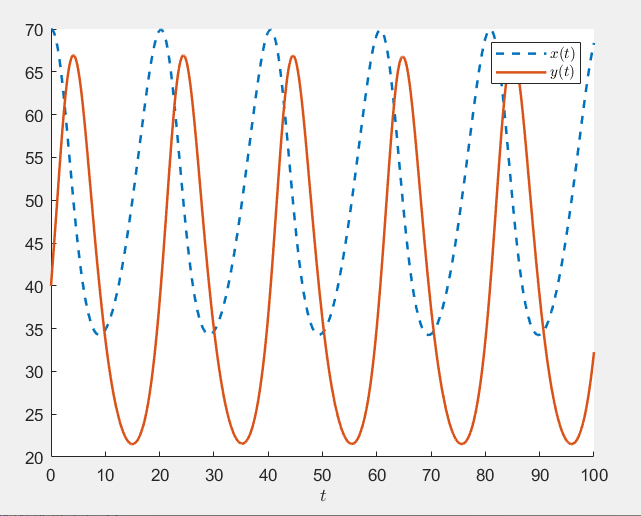
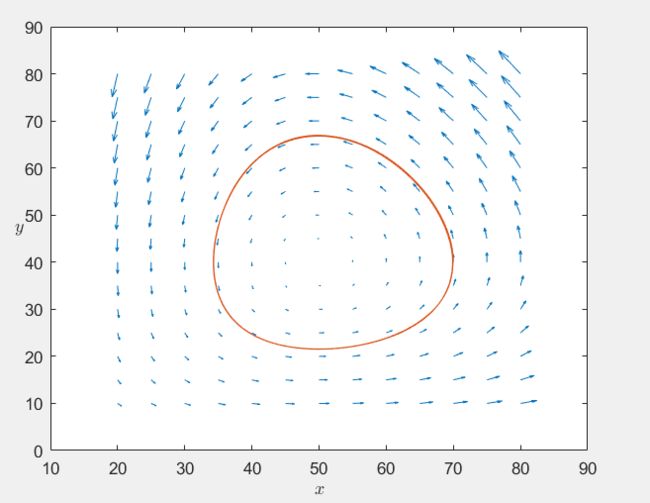
xlabel('day');ylabel('Demand for drugs')4.捕食者模型
% Diff_predator.m
clc,clear,close all
L=100;
x=20:5:80;y=10:5:80;[x,y]=meshgrid(x,y);
u=0.2*x-0.005*x.*y;v=-0.5*y+0.01*x.*y;
quiver(x,y,u,v),hold on
dxy=@(t,z)[0.2*z(1)-0.005*z(1)*z(2)
-0.5*z(2)+0.01*z(1)*z(2)];
sol=ode45(dxy,[0,L],[70;40]);
xt=@(t)deval(sol,t,1);
yt=@(t)deval(sol,t,2);
fplot(xt,yt,[0,L]),xlabel('$x$','Interpreter','latex')
ylabel('$y$','Interpreter','latex','Rotation',0)
figure(2),hold on
fplot(xt,[0,L],'--','LineWidth',1.5)
fplot(yt,[0,L],'LineWidth',1.5)
xlabel('$t$','Interpreter','latex')
legend({'$x(t)$','$y(t)$'},'Interpreter','latex')
fprintf('请在虚线上选取两个相邻的极小点\n')
[t1,xx]=ginput(2)
fprintf('请在实线上选取两个相邻的极小点\n')
[t2,yy]=ginput(2)
T1=diff(t1),T2=diff(t2)
[xt1,fx1]=fminbnd(xt,0,L)
[xt2,fx2]=fminbnd(@(t)-xt(t),0,L)
[yt1,fy1]=fminbnd(yt,0,20)
[yt2,fy2]=fminbnd(yt,20,40)
T=yt2-yt1
[yt3,fy3]=fminbnd(@(t)-yt(t),0,L)5.案例:放射性废料处理
% Diff_Radioactive.m
clc,clear,close all
syms m V rho g k s(t) v(t)
ds=diff(s);
eq=m*diff(s,2)-m*g+rho*g*V+k*diff(s)==0;
con1=s(0)==0;
con2=ds(0)==0;
con=[con1,con2];
s1=dsolve(eq,con);
s1=subs(s1,{m,V,rho,g,k},{239.46,0.2058,1035.71,9.8,0.6});
ss1=vpa(s1,7) %位移函数
eqq=m*diff(v)-m*g+rho*g*V+k*v==0;
conn=v(0)==0;
v1=dsolve(eqq,conn);
v1=subs(v1,{m,V,rho,g,k},{239.46,0.2058,1035.71,9.8,0.6});
vv1=vpa(v1,7) %速度函数
t1=solve(s1-90);t1=double(t1) %海底90m时间
vvv1=subs(v1,t,t1);vvv1=double(vvv1) %海底90m速度
eqqq=m*diff(v)-m*g+rho*g*V+k*v^2==0;
connn=v(0)==0;
v2=dsolve(eqqq,connn);
v2=subs(v2,{m,V,rho,g,k},{239.46,0.2058,1035.71,9.8,0.6});
v2=simplify(v2);vv2=vpa(v2,6) %速度函数
t2=solve(v2-12.2);t2=double(t2) %时间临界
s2=int(v2,0,t2);s2=double(s2) %位移临界
位移函数ss1 =
429.7444*t + 171511.0*exp(-0.002505638*t) - 171511.0
速度函数vv1 =
429.7444 - 429.7444*exp(-0.002505638*t)
到水深90m处需要时间t1 =
12.9994
此时速度vvv1 =
13.7720
速度vv2 =
20.7303*tanh(0.0519426*t)
若要速度<12.2m/s
则运动时间不能超过t2 =
13.0025
即位移不能超过s2 =
84.8439二.差分方程
1.Leslie种群模型
在某动物种群中,仅考察雌性动物的年龄和数量。
设雌性动物的最大生产年龄为L,等分为n个年龄组[0,L/n),[L/n,2L/n)...
设第i个年龄组的生育率为ai,存活率为bi
% fDiff_Leslie.m
clc,clear,syms k positive integer
x0=[500;1000;500];
L=[0,4,3;0.5,0,0;0,0.25,0];
L=sym(L);
x1=L*x0,x2=L*x1,x3=L*x2
p=charpoly(L)
r=roots(p)
[P,D]=eig(L)
xl=P*diag([1,0,0])*inv(P)*x0
tc=inv(P)*x0;c=tc(1)
x(k)=c * (3/2)^k * [18]
[ 6]
[ 1]三.数理统计
1.参数估计和假设检验
【1】区间估计
clc,clear
x0=[506 508 499 503 504 510 497 512
514 505 493 496 506 502 509 496];
x0=x0(:); %变为列向量
pd=fitdist(x0,'Normal') %正态分布拟合
ci=paramci(pd,'Alpha',0.05) %ci的第一列是均值的置信区间
[mu,s,muci,sci]=normfit(x0,0.05) %另一种方式求置信区间
pd =
NormalDistribution
正态分布
mu = 503.75 [500.445, 507.055]
sigma = 6.20215 [4.58156, 9.59901]
ci =
500.4451 4.5816
507.0549 9.5990
mu =
503.7500
s =
6.2022
muci =
500.4451
507.0549
sci =
4.5816
9.5990clc,clear
x1=[6.683,6.681,6.676,6.678,6.679,6.672];
x2=[6.661,6.661,6.667,6.667,6.664];
%均值检验和区间估计
[h1,p1,ci1,st1]=ttest(x1,mean(x1),"Alpha",0.1)
[h2,p2,ci2,st2]=ttest(x2,mean(x2),"Alpha",0.1)
%方差检验和区间估计
[h3,p3,ci3,st3]=vartest(x1,var(x1),"Alpha",0.1)
[h4,p4,ci4,st4]=vartest(x2,var(x1),"Alpha",0.1)
%双样本总体均值差的置信区间
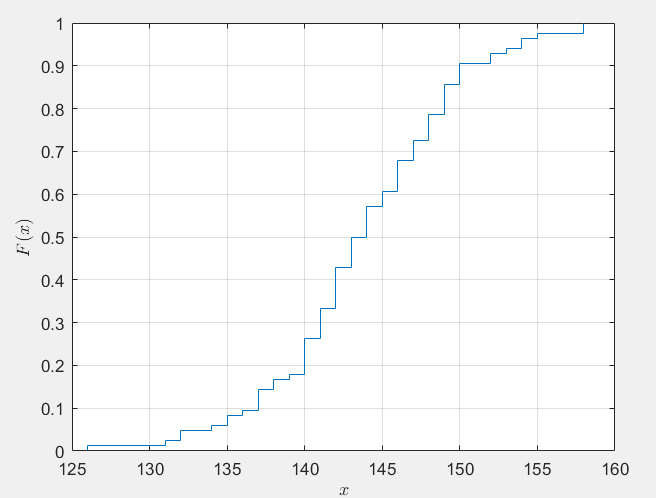
[h,p,ci,st]=ttest2(x1,x2,"Alpha",0.1)【2】经验分布函数
clc,clear,close all
a=readmatrix('ECDF.txt');a=a(~isnan(a));
[f,x]=ecdf(a);
ecdf(a)
grid on,xlabel('$x$','Interpreter','latex')
ylabel('$F(x)$','Interpreter','latex')
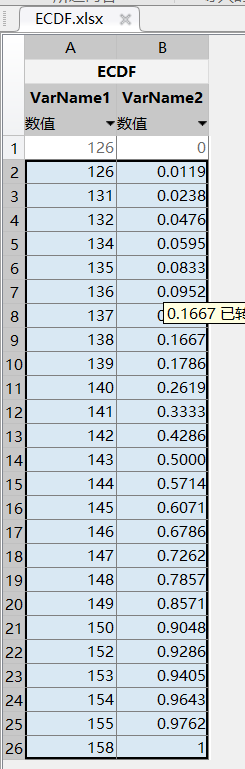
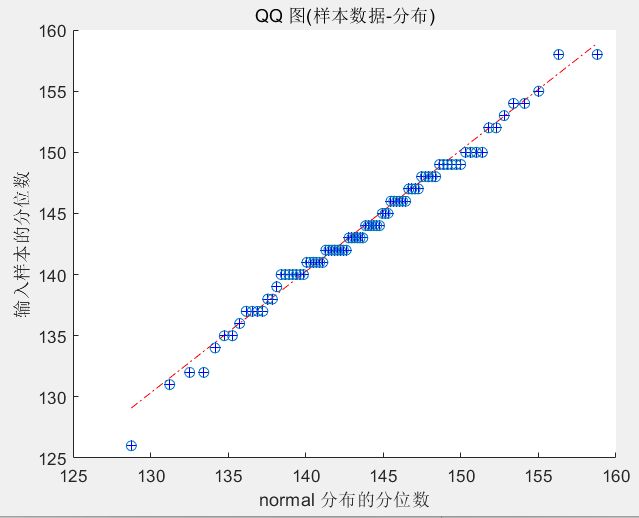
writematrix([x,f],'ECDF.xlsx')【3】Q-Q图
clc,clear,close all
a=readmatrix('ECDF.txt');a=a(~isnan(a));
pd=fitdist(a,'Normal'),qqplot(a,pd)
sa=sort(a);
n=length(a);pi=([1:n]-1/2)/n;
yi=norminv(pi,pd.mu,pd.sigma)';
hold on,plot(yi,sa,'o')
pd =
NormalDistribution
正态 分布
mu = 143.774 [142.478, 145.069]
sigma = 5.97051 [5.18413, 7.04034]【4】非参数检验
(1)卡方拟合优度检验
clc,clear
n=100;bins=[0:7]';mi=[36 40 19 2 0 2 1 0]';
pd=fitdist(bins,'Poisson','Frequency',mi) %泊松分布
expCounts=n*pdf(pd,bins) %期望频数
[h,p,st]=chi2gof(bins,'Ctrs',bins,'Frequency',mi,...
'Expected',expCounts,'NParams',1)
k2=chi2inv(0.95,st.df) %st.df为自由度(2)KS检验
clc,clear
a=readmatrix('ECDF.txt');a=a(~isnan(a));
pd=fitdist(a,'Normal')
[yn,xn]=ecdf(a);
y=cdf(pd,xn);
Dn=max(abs(yn-y))
LJ=1.36/sqrt(length(a))
[h,p,st,cv]=kstest(a,"CDF",pd)【5】秩和检验
clc,clear
x=[41.5 42.0 40.0 42.5 42.0 42.2 42.7 42.1 41.4];
y=[41.2 41.8 42.4 41.6 41.7 41.3];
yx=[y,x];yxr=tiedrank(yx)
yr=sum(yxr(1:length(y)))
[p,h,s]=ranksum(y,x)2.回归分析
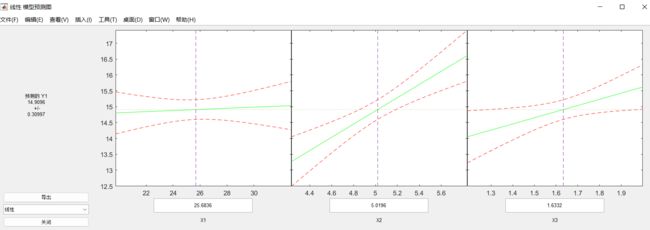
【1】多元二项式回归
clc,clear,close all
a=readmatrix('Regstats.txt')
Y=[a(:,2);a([1:end-1],7)];
X=[a(:,[3:5]);a([1:end-1],[8:10])];
c=regstats(Y,X)
beta=c.beta
F=c.fstat
m=3;n=length(Y);
Fa=finv(0.95,m,n-m-1)
T=c.tstat.t
Ta=tinv(0.975,n-m-1)
X23=X(:,[2,3]);
nc=regstats(Y,X23)
beta2=nc,beta
rstool(X,Y)
clc,clear,close all
a=readmatrix('Regstats.txt')
Y=[a(:,2);a([1:end-1],7)];
X=[a(:,[3:5]);a([1:end-1],[8:10])];
md=fitlm(X,Y)
md2=fitlm(X(:,[2,3]),Y)
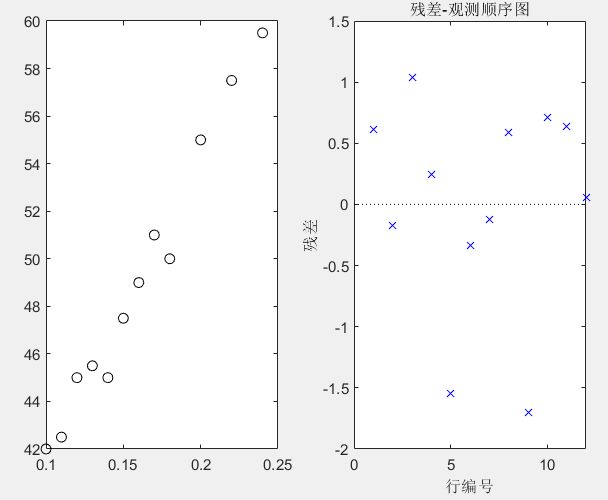
rstool(X,Y)clc,clear,close all
a=readmatrix('Regressionc.txt');
x=a(1,:)';y=a(2,:)';
subplot(121),plot(x,y,'ko')
md=fitlm(x,y);
[yh,yhint]=predict(md,x)
subplot(122),plotResiduals(md,'caseorder')
r=y-yh;ind=find(abs(r)>=1.5)
md2=fitlm(x,y,'Exclude',ind)【2】非线性回归
clc,clear
a=readmatrix('NLRegression.txt')
Y=[a(:,2);a([1:end-1],7)];
X=[a(:,[3:5]);a([1:end-1],[8:10])];
fun=@(beta,x)(beta(4)*x(:,2)-x(:,3)/beta(5))./(1+beta(1)*x(:,1)+...
beta(2)*x(:,2)+beta(3)*x(:,3));
beta0=[0.1,0.05,0.02,1,2]';
md=fitnlm(X,Y,fun,beta0)
betaci=coefCI(md)
[ypred,yci]=predict(md,X)【3】逐步回归
clc,clear
a=readmatrix('Stepwiselm.txt');
X=a(:,[1:end-1]);Y=a(:,end);
md0=fitlm(X,Y)
md1=fitlm(X,Y,'y~1+x1+x2+x4')
md2=fitlm(X,Y,'y~1+x1+x2')
md=stepwiseglm(X,Y,'y~1+x1+x2+x3+x4')