【学习笔记】组合计数

排列和组合

排列数（阶乘）

引入

让 $n$ 个人排成一排，求方案数

不妨这样思考：
第一个人先站队，这时他有 $n$ 个位置可以选，也就是有 $n$ 种方案
第二个人再站队，这时因为第一个人已经进去了，所以他有 $n-1$ 种站法
第三个人站队，同理有 $n-2$ 种站法
$\dots$
以此类推，第 $i$ 个人有 $n-i+1$ 种站法

那么根据乘法原理，总共的方案数就有
$$n\ast (n-1)\ast (n-2)\ast \cdots \ast 2\ast 1$$
也就是
$$n!$$

组合数（C）

引入

从 $n$ 个球里面选出 $m$ 个球，有多少种选法

可以这样想，把这 $n$ 个小球排成一排，每次选前 $m$ 个小球，那么根据排列数，有 $n!$ 种方案

但是我们不考虑小球的顺序，所以和前 $m$ 个小球的排列方式无关，和后面的 $n-m$ 个小球的顺序也没有关系

所以我们的方案数就是
$$C_n^m=\frac{n!}{m!(n-m)!}$$
其中 $C_n^m$ 表示从 $n$ 个球里面取 $m$ 个球的方案数（当然不限于取小球）

组合数递推公式

$$C_n^m=C_{n-1}^{m-1}+C_{n-1}^m$$

对于最后一个小球，有两种情况：取或者不取 那就分成了两个子问题
1.取最后一个小球，那问题就变成了在 $n-1$ 个小球种取 $m-1$ 个小球的方案数
2.不取最后一个小球，问题变为在 $n-1$ 个小球中取 $m$ 个小球的方案数

例题

题目传送门

题目大意

求有多少对i和j满足

• $0\le i\le n$
• $0\le j\le min(i,m)$
• 并且 $k$ 是 $C(i,j)$ 的约数

开始读入 $k,t$ ，接下来 $t$ 组数据，每组读入 $n,m$

分析

用组合数递推公式可以预处理出所有的方案，然后再直接求就行

复杂度爆了怎么办？用前缀和呗

Code

代码很丑陋，所以建议去题解区看大佬的代码

#include 
#define ll long long
#define ull unsigned long long
const int N = 2e3+10;
const int M = 1e4+10;
const int INF = 0x3f3f3f3f;

using namespace std;
int c[N][N],cnt[N][N];
int t, k;

int main(){
	cin >> t >> k;	
	for(int i = 1; i <= 2000;i++) c[i][i] = c[i][0] = 1; 
	
	for(int i = 1; i <= 2000; i++){
		for(int j = 1; j <= i; j++){
			if(j != i) 	c[i][j] = (c[i-1][j-1] + c[i-1][j]) % k;//j == i这里前面处理过了
			cnt[i][j]  = cnt[i-1][j] + cnt[i][j-1] - cnt[i-1][j-1] + !(c[i][j]);//前缀和
		}
		cnt[i][i+1]=cnt[i][i];//方便上面调用 这一步很重要，蒟蒻因为这一步调了半小时不知道问题再哪里
	}
	while(t--){
		int n, m;
		cin >> n >> m;
		if(m > n){
			cout << cnt[n][n] << endl;
		}else{
			cout << cnt[n][m] << endl;
		}
	}
	return 0;
}

可重排列和集合

可重排列

引入

有 $n$ 种颜色的球，第 $i$ 种颜色的球有 $a_i$ 个，请问有多少种排列方法

注意这里是要求所有球都要用上的

比如说有两种颜色的球，第 1 种有 2 个，第二种有 1 个，那么就有[1 1 2] [1 2 1] [2 1 1] 也就是 3 种方案

$$你看到了不该看的$$
我们令 $S={\sum }_{i=1}^n{a}_i$
把每种颜色的球一个一个的放进去，也就是说

• 第一步：放第 1 种颜色的球的时候，我们有 $C_S^{a_1}$ 种放法
• 第二步：放颜色 2，因为之前已经填好了 $a_1$ 个数了，还剩 $S-a_1$ 个空位，所以方案数为 $C_{S-a_1}^{a_2}$
• 第三步：放颜色 3,之前已经填好了 $a_1+a_2$ 个数了,还剩 $S-a_1-a_2$ 个空位,方案数为$C_{(S-a_1-a_2)}^{a_3}$

这样就可以推出答案为：

$$\begin{array}{rl}& C_S^{a_1}\cdot C_{S-a_1}^{a_2}\cdot C_{S-a_1-a_2}^{a_3}\cdots \\ & =\frac{S!}{a_1!\cdot (S-a_1)!}\times \frac{(S-a_1)!}{a_2!\cdot (S-a_1-a_2)!}\times \cdots \\ & =\frac{S!}{a_1!\cdot a_2!\cdot a_3!\cdots a_n!}\end{array}$$

其实还可以换一种方法理解
先把这 $S$ 个数随便排，有 $S!$ 种方案，但是因为有 $a_i$ 个球颜色相同，所以要除以 $a_i$

可重集合

引入

有 $n$ 种颜色的球，每种球有无限个，求选出 $m$ 个球的方案

学过初赛的大佬都知道，直接隔板法就可以做

差不多就是把 $m$ 个球分组，第几组代表第几类球选几个
也就是说在 $m$ 个球中插入$n-1$ 个隔板，两个隔板之间的球表示每一类选几个
这样，相当于一共有 $m+n-1$ 个空位，选出 $m$ 个放球，$n-1$ 个放隔板
方案数就是$$C_{(m+n-1)}^{(n-1)}$$

圆排列

引入

$n$ 个人站成一圈，有几种站法

其实思路很简单，就是求出全排列然后再除以 $n$ （因为一个圈可以有 $n$ 种拆分方式）

错排问题

引入

求出1到 $n$ 的排列中每个数都不在自己位置上的排列个数

这题也可以根据递推求解

假设第 $n$ 个小朋友坐在了第 $i$ 个小朋友的位置上，分成两个子问题：

1. 第 $i$ 个小朋友也坐在第 $n$ 个小朋友的位置上，问题就变成了求 $n-2$ 个小朋友的错排
2. 第 $i$ 个小朋友没有坐在第 $n$ 个小朋友的位置上，问题变成了求 $n-1$ 个小朋友的错排

那么就得到了递推式子：
$$f_n=(n-1)\times (f_{n-2}+f_{n-1})$$

二项式定理

$$(x+y{)}^n=\sum _{i=0}^n(\genfrac{}{}{0ex}{}{n}{i})x^i{y}^{n-i}$$

证明

假设
$$(x+y{)}^{n-1}=\sum _{i=0}^{n-1}(\genfrac{}{}{0ex}{}{n-1}{i})x^i{y}^{n-1-i}$$
$$\begin{array}{rl}& (x+y{)}^n=(x+y)(x+y{)}^{n-1}\\ & =(x+y)\sum _{i=0}^{n-1}\left(\genfrac{}{}{0ex}{}{n-1}{i}\right)x^i{y}^{n-1-i}\\ & =\sum _{i=0}^{n-1}\left(\genfrac{}{}{0ex}{}{n-1}{i}\right)x^{i+1}{y}^{n-1-i}+\sum _{i=0}^{n-1}\left(\genfrac{}{}{0ex}{}{n-1}{i}\right)x^i{y}^{n-i}\\ & =\sum _{i=1}^n\left(\genfrac{}{}{0ex}{}{n-1}{i-1}\right)x^i{y}^{n-i}+\sum _{i=0}^{n-1}\left(\genfrac{}{}{0ex}{}{n-1}{i}\right)x^i{y}^{n-i}\end{array}$$
因为$\left(\genfrac{}{}{0ex}{}{n-1}{i-1}\right)+\left(\genfrac{}{}{0ex}{}{n-1}{i}\right)=\left(\genfrac{}{}{0ex}{}{n}{i}\right)$,所以
$$(x+y{)}^n=\sum _{i=0}^n(\genfrac{}{}{0ex}{}{n}{i})x^i{y}^{n-i}$$

如何理解？

有 $x+y$ 种颜色，给 $n$ 个球染色，一共有 $(x+y{)}^n$种染色方法
而这 $x+y$ 种颜色可以分为 $x$ 种深色和 $y$ 种浅色
我们枚举有 $i$ 个球染成深色，$n-i$ 个球染成浅色
方案数就是 $\left(\genfrac{}{}{0ex}{}{n-1}{i}\right)x^i{y}^{n-i}$

卢卡斯定理

当 $p$ 为质数时
$$\left(\genfrac{}{}{0ex}{}{n}{m}\right)modp=\left(\genfrac{}{}{0ex}{}{\left[\frac{n}{p}\right]}{\left[\frac{m}{p}\right]}\right)\left(\genfrac{}{}{0ex}{}{n\mathrm{mod}p}{m\mathrm{mod}p}\right)\mathrm{mod}p$$

例题卢卡斯定理

#include 
#define ll long long
#define ull unsigned long long
#define int ull
const int N = 1e6+10;
const int M = 1e4+10;
const int INF = 0x3f3f3f3f;

using namespace std;
int ksm(int a, int b, int mod){
	int x = a,ans = 1;
	while(b){
		if(b & 1){
			ans = ans * x % mod;
		}
		x = x * x % mod;
		b >>= 1;
	}
	return ans;
}
ull C(int n, int m, int mod){
	if(n < m) return 0;
	int a =1, b = 1;
	for(int i = 1; i <= n; i++) a = a * i % mod;
	for(int i = 1; i <= m; i++) b = b * i % mod;
	for(int i = 1; i <= n - m; i++) b = b * i % mod;
	
	return a * ksm(b,mod-2,mod) % mod;
//	return a / b % mod;
}
ull lucas(int n, int m, int mod){
	if(n < mod && m < mod) return C(n,m,mod);
	return lucas(n/mod, m/mod,mod) * C(n % mod,m % mod,mod) % mod;
}
signed main(){
	int t;
	cin >> t;
	while(t--){
		int n, m, p;
		cin >> n >> m >> p;
		cout << lucas(n+m,n, p) << endl;
	}
	return 0;
}

容斥原理

引入

10个小朋友中，有8个会线段树，有5个会树状数组，问既会线段树又会树状数组的有多少人

很显然这是一道小学题目，当然也是容斥原理的典型应用

维恩图

这玩意应该很熟悉了吧，就是几个圈，重叠的部分表示共有的部分

集合

这里不知道集合是什么的自行百度罢（）

让我们看看交集和并集在维恩图上的表示

设会树状数组的是集合 $A$， 会线段树的是集合 $B$ ，那么 $A\cup B$ 就是所有人， $A\cap B$ 就是线段树和树状数组都会的人

从这里我们可以发现什么？

我们可以将并集用交集表示，将交集用并集表示：
$$\begin{gathered} |A|+|B|-|A\cap B|=|A\cup B| \\ |A|+|B|-|A\cup B|=|A\cap B| \end{gathered}$$

扩展到三个集合

当我们求三个集合的并集的时候
$$|A\cup B\cup C|=|A|+|B|+|C|-|A\cup B|-|A\cup C|+|A\cap B\cap C|$$

扩展到 n 个集合

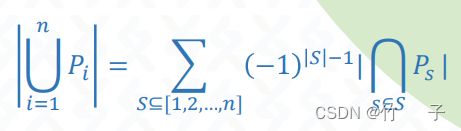
这里的 $P$ 是集合，其中 $(-1{)}^{|S|-1}$ 是容斥系数，也就是上面三个集合中的加减

引例

有 $n$ 种颜色的小球，每种小球有一个数量限制，现在取出 $m$ 个小球，有几种取法？

是不是和上面隔板法那道题很像？只是这次加入了数量限制

现在再思考一下，求出所有满足条件的方案数和求出所有不满足条件的方案数哪个容易？
肯定是不满足条件的容易，因为只要有一种小球超出限制就不满足了，而满足条件的需要考虑所有小球

满足条件的方案数不就是所有方案减去不满足的方案吗

这样问题就转化成了求不满足的方案数，用容斥原理就行

P1450 硬币购物

首先没有硬币限制的时候就是一个完全背包的板子，用完全背包求出来就行
然后使其中几种硬币超出限制，按照公式求出不满足的方案数

#include 
#define ll long long
#define ull unsigned long long
const int N = 1e5+10;
const int M = 1e4+10;
const int INF = 0x3f3f3f3f;

using namespace std;
int c[5],d[5],n,s;
ll dp[N];
int main(){
	cin >> c[0] >> c[1] >> c[2] >> c[3] >> n;
	dp[0] = 1;
	for(int i = 0; i < 4;i++){
		for(int j = c[i]; j <= 100000; j++){
			dp[j] += dp[j-c[i]];
		}
	}
	while(n--){
		cin >> d[0] >> d[1] >> d[2] >> d[3];
		cin >> s;
		ll ans = 0;
		for(int i = 0; i < (1 << 4);i++){
			int m = s;
			for(int j = 0; j < 4; j++){
				if(i>>j & 1){
					m -= c[j] * (d[j]+1);
				}
			}
			if(m >= 0){
				ans += dp[m] * (__builtin_popcount(i)&1?-1:1);
			}
		}
		cout << ans << endl;
	}
	return 0;
}

这里的 $\_\_builtin\_popcount(i)$ 就是数二进制下 $i$ 中1的个数，也就是计算容斥系数