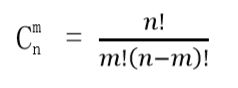从n个不同元素中取出m个元素排列组合

01. 问题

问题01. 算法: 从n个不同元素中取出m个元素的排列数是多少? 这些排列分别是什么? (其中: n > 0; 0 < m ≤ n;)

问题02. 算法: 从n个不同元素中取出m个元素的组合数是多少? 这些组合分别是什么? (其中: n > 0; 0 < m ≤ n;)

02. 概念

排列组合是组合学最基本的概念.

所谓排列, 就是指从给定个数的元素中取出指定个数的元素进行排序. 组合则是指从给定个数的元素中仅仅取出指定个数的元素, 不考虑排序.

a. 定义及公式

排列的定义:

从n个不同元素中, 任取m(m≤n,m与n均为自然数,下同)个元素按照一定的顺序排成一列, 叫做从n个不同元素中取出m个元素的一个排列;

从n个不同元素中取出m(m≤n)个元素的所有排列的个数, 叫做从n个不同元素中取出m个元素的排列数, 用符号 A(n,m)表示.

计算公式:

A(n,m) = n! / (n-m)!

此外规定:

0! = 1

n! = (n-1)(n-2)...1

组合的定义:

从n个不同元素中, 任取m(m≤n)个元素并成一组, 叫做从n个不同元素中取出m个元素的一个组合;

从n个不同元素中取出m(m≤n)个元素的所有组合的个数, 叫做从n个不同元素中取出m个元素的组合数. 用符号 C(n,m) 表示.

计算公式:

C(n,m) = n! / (m! * (n-m)!)

C(n,m) = C(n,n-m)

03. Java实现

a. 排列

使用递归运算解决

/**
 * 从6个不同数字取出k个数字的排列
 * A(n, m) = n! / (n−m)! (n个数取m个排列) permutation and combination
 */
@Test
public void permAcomb2() {
    int[] numArray = {1, 2, 3, 4, 5, 6};
    permutation2(numArray, 0, numArray.length - 3);

    // 打印验证
    System.out.println(allSorts2);
    System.out.println(allSorts2.size());
}
private static List allSorts2 = new ArrayList<>();
private static void permutation2(int[] nums, int start, int end) {
    if (start == end) { // 当只要求对数组中一个数字进行全排列时，只要就按该数组输出即可
        allSorts2.add(join(nums, "", 0, end)); // 将新的排列组合存放起来
    } else {
//      for (int i = start; i <= end; i++) { // 注释代码为A(n, n)
        for (int i = start; i <= nums.length; i++) {
            int temp = nums[start]; // 交换数组第一个元素与后续的元素
            nums[start] = nums[i];
            nums[i] = temp;
            permutation2(nums, start + 1, end); // 后续元素递归全排列
            nums[i] = nums[start]; // 将交换后的数组还原
            nums[start] = temp;
        }
    }
}
private static String join(int[] arr, String spor, int ks, int js) {
    StringBuilder sb = new StringBuilder();
    for (int i = ks; i < js; i++) {
        sb.append(arr[i]).append(spor);
    }
    return sb.toString();
}

b. 组合

使用递归运算解决

/**
 * 从8个不同数字取出k个数字的组合
 * C(n, m) = n! / (m! * (n−m)!) (n个数取m个组合) combination
 */
@Test
public void comb() {
    int[] com = {1, 2, 3, 4, 5, 6, 7, 8};
    int k = 3;
    if (k > com.length) {
        return;
    }
    combine(0, k, com);
}

private static ArrayList tmpArr = new ArrayList<>();

private static void combine(int index, int k, int[] arr) {
    if (k == 1) {
        for (int i = index; i < arr.length; i++) {
            tmpArr.add(arr[i]);
            System.out.println(tmpArr.toString());
            tmpArr.remove((Object) arr[i]);
        }
    } else if (k > 1) {
        for (int i = index; i <= arr.length - k; i++) {
            tmpArr.add(arr[i]);
            combine(i + 1, k - 1, arr);
            tmpArr.remove((Object) arr[i]);
        }
    }
}

附:

组合思维导图