线性结构:栈
文章目录
-
-
- 栈定义
- 栈应用
-
- 括号匹配
- 十进制转换
- 表达式转换
- 后缀表达式求值
-
栈定义
栈顶进栈顶出
一种有次序的数据项集合,在栈中,数据项的加入和移除都仅发生在同一端。
这一端叫栈“顶top”,另一端叫栈“底base“
距离栈底越近的数据项,留在栈中的时间就越长
而最新加入栈的数据项会被最先移除
这种次序通常称为==“后进先出LIFO”==:Last in First out
这是一种基于数据项保存时间的次序,时间越短的离栈顶越近,而时间越长的离栈底越近
栈的特性:反转次序
进栈和出栈次序正好相反
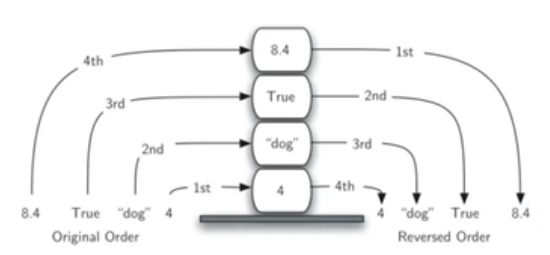
- 例如,浏览器后退按钮,最先back最近访问的网页;撤销按钮
抽象数据类型Stack
抽象数据类型“栈”是一个有次序的数据集,每个数据项仅从“栈顶”一端加入到数据集中、从数据集中移除,栈具有后进先出LIFO的特性
栈操作
- Stack():创建一个空栈,不包含任何数据项
- push(item):将item加入栈顶,无返回值
- pop():将栈顶数据项移除,并返回,栈被修改
- peek(): “窥视”栈顶数据项,返回栈顶的数据项但不移除,栈不被修改
- isEmpty():返回栈是否为空栈
- size():返回栈中有多少个数据项
操作样例

实现ADT Stack
在清楚地定义了抽象数据类型Stack之后,我们看看如何用Python来实现它
Python的面向对象机制,可以用来实现用户自定义类型
- 将ADT Stack实现为Python的一个Class
- 将ADT Stack的操作实现为Class的方法
- 由于Stack是一个数据集,所以可以采用Pythor的原生数据集来实现,我们选用最常用的数据集List来实现
一个细节:Stack的两端对应list设置可以将List的任意一端(index=0或者-1)设置为栈顶
我们选用List的末端(index=-1)作为栈顶这样栈的操作就可以通过对list的append和pop来实现
Python实现代码
栈顶在右侧(push/pop的复杂度为0(1))
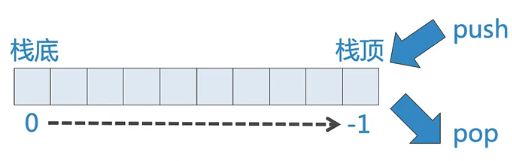
- 保存为stack.py,需要使用栈时,
from stack import Stack
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item): # 入栈
self.items.append(item)
def pop(self): # 出栈并返回数据项
return self.items.pop()
def peek(self): # 返回栈底数据
return self.items[len(self.items) - 1]
def size(self):
return len(self.items)
栈顶在左侧(push/pop的复杂度为0(n))
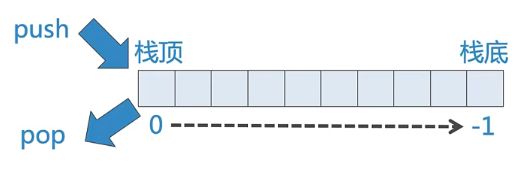
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item): # 入栈
self.items.insert(0, item)
def pop(self): # 出栈并返回数据项
return self.items.pop(0)
def peek(self): # 返回栈底数据
return self.items[0]
def size(self):
return len(self.items)
不同实现方案保持了ADT接口的稳定性
栈应用
括号匹配
简单括号匹配
从左到右扫描括号串,最新打开的左括号,应该匹配最先遇到的右括号这样,第一个左括号(最早打开),就应该匹配最后一个右括号(最后遇到)这种次序反转的识别,正好符合栈的特性
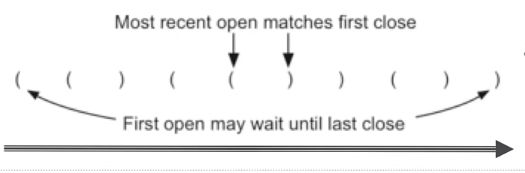
from stack import Stack
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol == '(':
s.push(symbol) # 左括号入栈
elif symbol == ')':
if s.isEmpty():
balanced = False
else:
s.pop() # 左括号出栈
index += 1
if balanced and s.isEmpty(): # 有足够多的左括号匹配右括号,并且无剩余左括号,则正好全匹配
return True
else:
return False
print(parChecker('((()))')) # True
print(parChecker('((()')) # False
通用括号匹配算法
- 改进:碰到各种左括号仍入栈,碰到各种右括号需要判断栈顶的左括号是否和右括号属于同一类
from stack import Stack
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol in '([{':
s.push(symbol) # 左括号入栈
elif symbol in ')]}':
if s.isEmpty():
balanced = False
else:
top = s.pop() # 左括号栈顶数据出栈,返回栈顶数据
if not matches(top, symbol): # 右括号与栈顶左括号不是一类匹配失败
balanced = False
index += 1
if balanced and s.isEmpty(): # 有足够多的左括号匹配右括号,并且无剩余左括号,则正好全匹配
return True
else:
return False
def matches(left, right):
lefts = '([{'
rights = ')]}'
return lefts.index(left) == rights.index(right) # 判断左右括号是否属于一类
print(parChecker('{[()]}')) # True
print(parChecker('{[[))}')) # False
十进制转换
十进制转二进制
二进制是计算机原理中最基本的概念,作为组成计算机最基本部件的逻辑门电路,其输入和输出均仅为两种状态:0和1
- 但十进制是人类传统文化中最基本的数值概念,如果没有进制之间的转换,人们跟计算机的交互会相当的困难
十进制转换为二进制,采用的是“除以2求余数”的算法
- 将整数不断除以2,每次得到的余数就是由低到高的二进制位
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OTElnzwf-1689826225640)(./image/image-20230718085818600.png)]
"除以2"的过程,得到的余数是从低到高的次序,而输出则是从高到低,所以需要一个栈来反转次序

from stack import Stack
def divideBy2(decNumber):
remstack = Stack()
while decNumber > 0: # 被除数大于零
rem = decNumber % 2 # 余数
remstack.push(rem) # 余数入栈
decNumber = decNumber // 2 # 新被除数为商
binString = '' # 存放二进制的字符串
while not remstack.isEmpty(): # 从栈顶依次取值加入binSting
binString = binString + str(remstack.pop())
return binString
十进制转换为二进制的算法,很容易可以扩展为转换到任意N进制
- 只需要将“除以2求余数”算法改为“除以N求余数”算法就可以计算机中
- 另外两种常用的进制是八进制和十六进制
十进制转换十六进制以下任意进制
from stack import Stack
def baseConverter(decNumber, base): # base为转换后的进制
remstack = Stack()
digits = '0123456789ABCDEF' # 十六进制表
while decNumber > 0: # 被除数大于零
rem = decNumber % base # 余数
remstack.push(rem) # 余数入栈
decNumber = decNumber // base # 新被除数为商
newString = ''
while not remstack.isEmpty():
newString = newString + digits[remstack.pop()] # 从表中取对应值
return newString
print(baseConverter(29, 16)) # 1D
表达式转换
中缀表达式
我们通常看到的表达式象这样:B * C,很容易知道这是B乘以C
这种操作符(operator)介于操作数(operand)中间的表示法,称为“中缀表示法但有时候中缀表示法会引起混淆,如"A+B * C"
- 是A+B然后再乘以C还是B*C然后再去加A
操作符优先级概念
- 规定高优先级的操作符先计算相同优先级的操作符从左到右依次计算这样A+B*C就没有疑义是A加上B与C的乘积
同时引入了括号来表示强制优先级,括号的优先级最高,而且在嵌套的括号中,内层的优先级更高
- 这样(A+B)*C就是A与B的和再乘以C
全括号中缀表达式
虽然人们已经习惯了这种表示法,但计算机处理最好是能明确规定所有的计算顺序,这样无需处理复杂的优先规则
引入全括号表达式:在所有的表达式项两边都加上括号
- A+B * C+D,应表示为((A+(B*C))+D)
前缀后缀表达式
例如中缀表达式A+B
- 将操作符移到前面,变为“+AB”或者将操作符移到最后,变为“AB+”
我们就得到了表达式的另外两种表示法:“前缀”和“后缀”表示法
-
以操作符相对于操作数的位置来定义
-
A+B*C 将变成前缀 +A*BC 和 后缀ABC*+
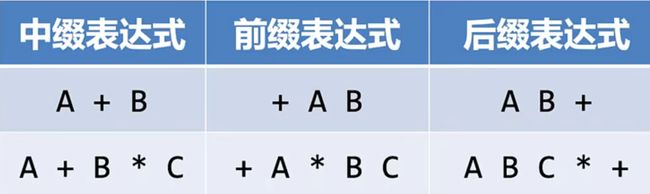
- 离操作数越近的操作符先运行,越远的后执行
中缀表达式转换为前缀后缀形式
看子表达式(B*C)的右括号,如果把操作符*移到右括号的位置,替代它,再删去左括号,得到BC*,这个正好把子表达式转换为后缀形式
- 进一步再把更多的操作符移动到相应的右括号处替代之,再删去左括号,那么整个表达式就完成了到后缀表达式的转换
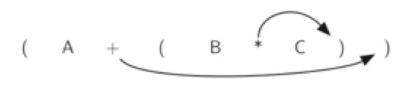
-
反之把操作符移动到左括号的位置替代之,然后删掉所有的右括号,也就得到了前缀表达式
-
将中缀表达式转换为全括号形式通用方法
- 将所有的操作符移动到子表达式所在的左括号(前缀)或者右括号(后缀)处,替代之,再删除所有的括号
通用中缀转后缀算法
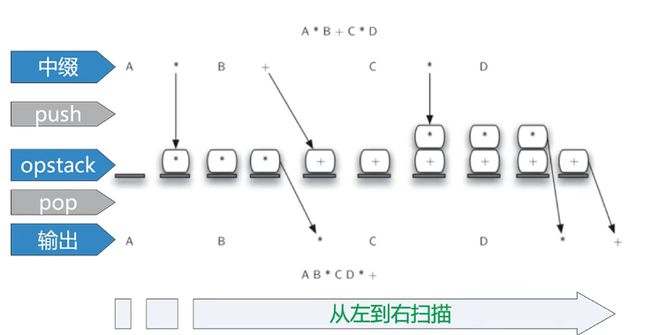
在从左到右扫描逐个字符扫描中缀表达式的过程中,采用一个栈来暂存未处理的操作符
这样,栈顶的操作符就是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再行处理。
- 首先,创建空栈opstack用于暂存操作符,空表postfixList用于保存后缀表达式
- 将中缀表达式转换为单词(token)列表
A + B * C = split => ['A', '+', 'B', '*', 'C']
算法流程
从左到右扫描中缀表达式单词列表
-
如果单词是操作数,则直接添加到后缀表达式列表的末尾
-
如果单词是左括号“(”,则压入opstack栈顶
-
如果单词是右括号“)”,则反复弹出opstack栈顶操作符,加入到输出列表末尾,直到碰到左括号
-
如果单词是操作符“*/±”,则压入opstack栈顶
-
但在压入之前,要比较其与栈顶操作符的优先级
-
如果栈顶的高于或等于它,就要反复弹出栈顶操作符,加入到输出列表末尾
-
直到栈顶的操作符优先级低于它
-
-
中缀表达式单词列表扫描结束后,把opstack栈中的所有剩余操作符依次弹出,添加到输出列表末尾
-
把输出列表再用join方法合并成后缀表达式字符串,算法结束。
from stack import Stack
def infix_to_postfix(infixexpr):
# 记录操作符优先级
prec = {}
prec['*'] = 3
prec['/'] = 3
prec['+'] = 2
prec['-'] = 2
prec['('] = 1
op_stack = Stack()
post_fixlist = [] # 后缀列表
token_list = infixexpr.split() # 解析表达式到单词
for token in token_list: # 扫描单词列表
if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
post_fixlist.append(token) # 操作数直接放到列表中
elif token == "(": # 遇到左括号压入栈
op_stack.push(token)
elif token == ')': # 遇到右括号弹出栈顶元素
top_token = op_stack.pop()
while top_token != "(": # 如果栈顶元素不是左括号,将栈顶元素添加到列表中。直到栈顶元素是左括号为止
post_fixlist.append((top_token))
top_token = op_stack.pop() # 弹出栈顶元素保存为top_token
else: # 如果遇到操作符
while (not op_stack.isEmpty()) and (prec[op_stack.peek()] >= prec[token]): # 栈非空情况下,只要栈顶元素优先级大于token就弹出,添加到列表中
post_fixlist.append(op_stack.pop())
op_stack.push(token) # token优先级比栈顶大就压入栈
while not op_stack.isEmpty(): # 弹出剩余栈内元素添加到列表中直至为空
post_fixlist.append(op_stack.pop())
return " ".join(post_fixlist)
print(infix_to_postfix("( A + B ) * ( C + D )"))
# A B + C D + *
print(infix_to_postfix("( A + B ) * C"))
# A B + C *
print(infix_to_postfix("A + B * C"))
# A B C * +
后缀表达式求值
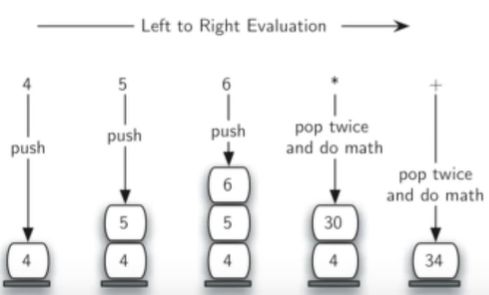
在对后缀表达式从左到右扫描过程中,操作符在操作数后面,所以要暂存操作数,在碰到操作符的时候,再将暂存的两个操作数进行实际计算。
- 栈的特性:操作符只作用于离他最近的两个操作数
- 注意先压入为左操作数,后为右操作数,弹出时相反,先弹出右操作数,然后是左操作数
- 中间结果再压入栈顶,继续扫描后续符号、
- 当所有操作符处理完毕,栈中剩余就是表达式值
from stack import Stack
def postfix_eval(postfix_expr):
operand_stack = Stack()
token_list = postfix_expr.split()
for token in token_list: # 扫描单词列表
if token in "0123456789":
operand_stack.push(int(token))
else: # 如果遇到操作符
operand2 = operand_stack.pop()
operand1 = operand_stack.pop()
result = domath(token, operand1, operand2)
operand_stack.push(result)
return operand_stack.pop()
def domath(op, op1, op2):
if op == "*":
return op1 * op2
elif op == "/":
return op1 / op2
elif op == "+":
return op1 + op2
else:
return op1 - op2
print(postfix_eval("3 4 5 * +"))
# 23