非线性质量弹簧阻尼器的神经网络仿真研究（Matlab代码&Simulink仿真实现）

 

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码、Simulink仿真实现

---

1 概述

非线性质量弹簧阻尼器（Nonlinear Mass-Spring-Damper，NMSD）是一种常见的振动控制装置，广泛应用于工程结构的减震和振动控制中。为了进行NMSD的神经网络仿真研究，以下步骤进行：

1. 数据收集：收集NMSD系统的输入和输出数据。输入可以是外部激励力或加速度，输出可以是系统的位移、速度或加速度响应。

2. 数据预处理：对收集到的数据进行预处理，包括数据清洗、滤波、降采样等。确保数据的质量和准确性。

3. 神经网络模型选择：根据仿真的目标和问题特点，选择合适的神经网络模型。常用的模型包括多层感知机（Multi-Layer Perceptron，MLP）、卷积神经网络（Convolutional Neural Network，CNN）等。

4. 数据划分：将数据集划分为训练集、验证集和测试集。通常采用交叉验证的方法，确保模型的泛化能力。

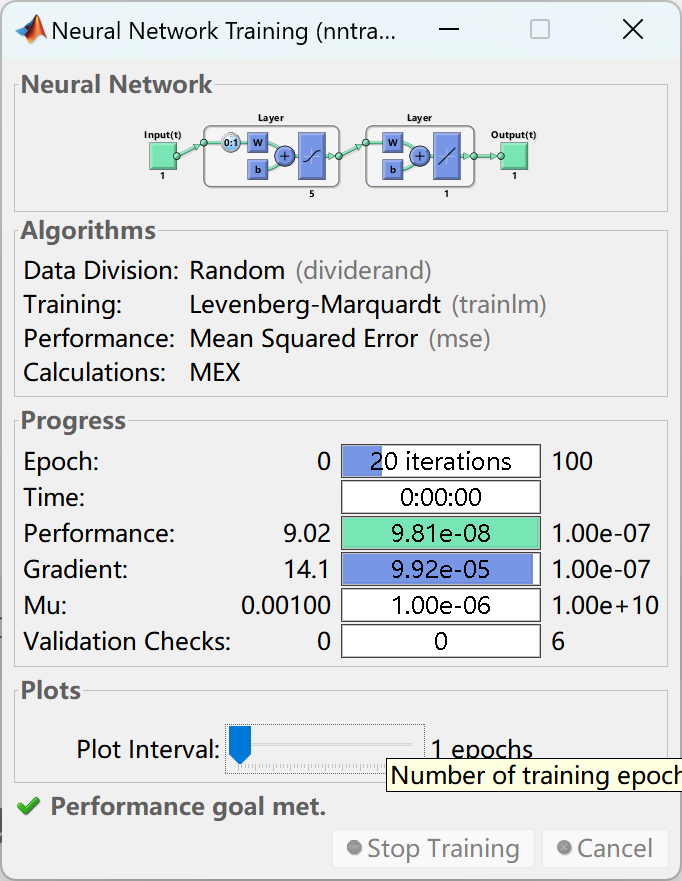
5. 网络训练：使用训练集对选定的神经网络模型进行训练。可以采用梯度下降法等优化算法来最小化损失函数，调整网络的权重和参数。

6. 模型评估：使用验证集评估训练得到的模型的性能，包括准确度、误差等指标。如果需要改进模型，可以通过调整网络结构、超参数等来优化模型。

7. 模型测试：使用测试集对优化后的模型进行测试，评估其在未见过的数据上的性能表现。可以比较模型的预测结果和实际观测值，分析模型的准确度和可靠性。

在进行非线性质量弹簧阻尼器神经网络仿真研究时，需要充分理解NMSD系统的原理和特性，并对神经网络的训练过程和参数调整有一定的了解。同时，根据具体问题的需求，可以进行更加深入和复杂的模型设计与研究。

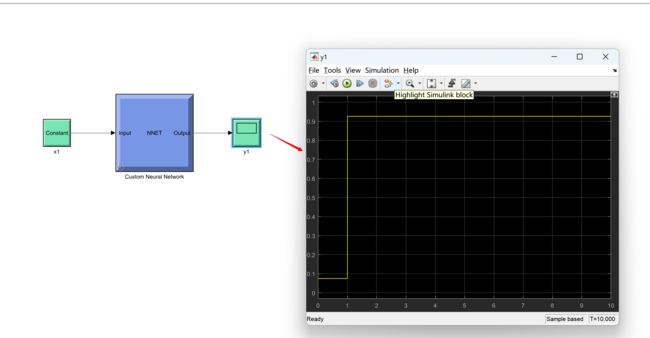
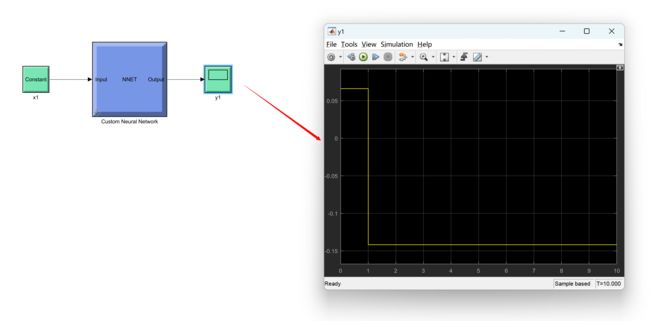
2 运行结果

 

 

 

 主函数代码：

function[]=main()

close all
clear all
clc

%Call network creating functions
Bnet=NNdamper();
Snet=NNspring();
close all

%Time
timestep=.1;
t=0:timestep:5;
st=size(t,2);
%Choice of Forcing Function

F=2*sin(2*t).*exp(-t/2);

for i=floor(st/2):st
F(1,i)=0;
end

%F=zeros(size(t));
%plot(t,F)

%size init.
pos=zeros(size(t));
vel=pos;
B=pos;
K=pos;
D=pos;

pdot_real=pos;
p_real=pos;
pos_real=pos;
vel_real=pos;
p=pos;
pdot=pos;

%I.C's!
pos(1)=0;%redundant but clear, ok?redundant but clear, ok?
vel(1)=0;
pos_real(1)=pos(1);
vel_real(1)=vel(1);

mass=5;%tons!
p(1)=vel(1)*mass;
p_real=p(1);

K0=sim(Snet,0);% In order to cancel(reduce) steady state error due to neural nets.
B0=sim(Bnet,0);

for i=1:size(t,2)-1;
    
    D(i)=Dtanal(i);
    % D(i)=0;
    
    K(i)=sim(Snet,pos(i));
    B(i)=sim(Bnet,vel(i));
    
    pdot(i+1)=F(1,i)+D(i)-K(i)-B(i)+K0+B0;
    
    %Momentum integrator
    
    p(i+1)=p(i)+pdot(i+1)*timestep;
    
    vel(i+1)=p(i)/mass;
    
    %Vel integrator
    
    pos(i+1)=pos(i)+vel(i+1)*timestep;
    
    
end

%Real solution
for i=1:size(t,2)-1;
    
    pdot_real(i+1)=F(1,i)+D(i)-Fxanal(pos_real(i))-Bvanal(vel_real(i));
    
    %Momentum integrator
    
    p_real(i+1)=p_real(i)+pdot_real(i+1)*timestep;
    
    vel_real(i+1)=p_real(i)/mass;
    
    %Vel integrator
    pos_real(i+1)=pos_real(i)+vel_real(i+1)*timestep;
    
    
end

%-------------------------------------------------
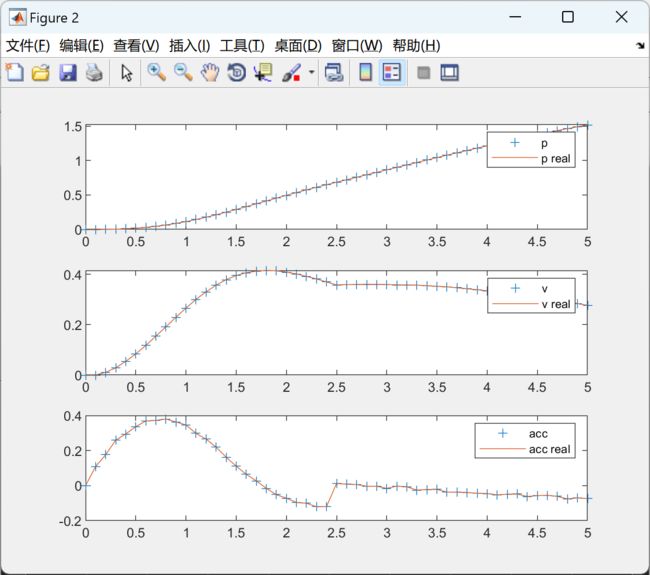
figure(2)

subplot(3,1,3);

plot(t,pdot/mass,'+',t,pdot_real/mass);
legend('acc','acc real');

subplot(3,1,2);

plot(t,vel,'+',t,vel_real);
legend('v','v real');

subplot(3,1,1);
plot(t,pos,'+',t,pos_real);
legend('p','p real');

%-------------------------------------------------
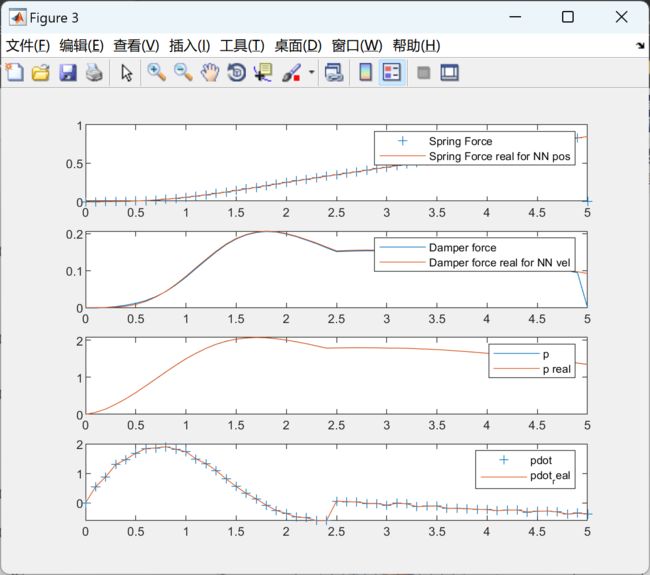
figure(3)

subplot(4,1,1);
plot(t,K,'+',t,Fxanal(pos));
legend('Spring Force','Spring Force real for NN pos');

subplot(4,1,2);
plot(t,B,t,Bvanal(vel));
legend('Damper force','Damper force real for NN vel')

subplot(4,1,3);
plot(t,p,t,p_real);
legend('p','p real')

subplot(4,1,4);
plot(t,pdot,'+',t,pdot_real);
legend('pdot','pdot_real');

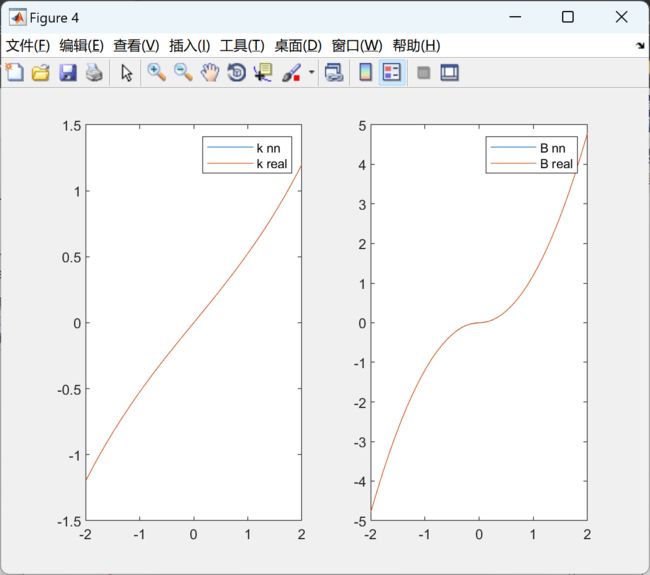
figure(4)
a=linspace(-2,2);
subplot(1,2,1)
plot(a,sim(Snet,a),a,Fxanal(a))
legend('k nn', 'k real')

subplot(1,2,2)
plot(a,sim(Bnet,a),a,Bvanal(a))
legend('B nn', 'B real')

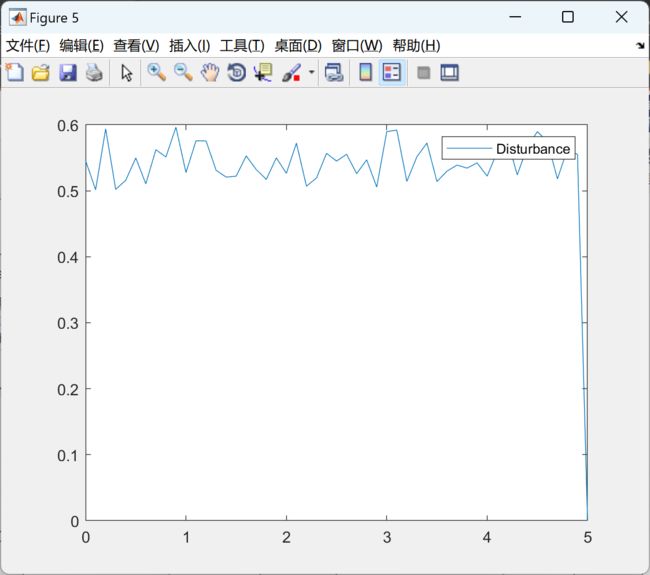
figure(5)
plot(t,D)
legend('Disturbance')

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]谭蔚,贾占斌,聂清德.弹簧阻尼器在塔器防振中的应用[J].化学工程,2013,41(12):16-19+34.

[2]周瑜,李敬豪.基于自适应弹簧阻尼器的变频凝泵低频共振治理方法研究[J].科技风,2023(07):58-61.DOI:10.19392/j.cnki.1671-7341.202307019.

[3]梁红玉,屈铁军.基于弹簧阻尼器的风机桥架的减振设计[J].北方工业大学学报,2011,23(01):84-88.

4 Matlab代码、Simulink仿真实现