秋招LeetCode刷题Day2 -- DFS深度优先算法之岛屿专题

---

知识总结

今天做了一系列岛屿相关的问题, 熟练掌握DFS算法
模板如下

dfs(int[][] grid, int i, int j){
	if(i < 0 || j < 0 || i >= grid.length || j >= grid[0].length){
		// 操作
	}
	if(grid[i][j] == 1) {
		// 操作
	}
	grid[i][j] = 0; // 淹没
	dfs(grid, i+1, j);
	dfs(grid, i-1, j);
	dfs(grid, i, j+1);
	dfs(grid, i, j)-1;
}

---

Leetcode 200. 岛屿数量

题目链接

题目说明

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

代码说明

经典题型, 以这个题目为基础, 之后产生种种变化

class Solution {

    public int numIslands(char[][] grid) {
        // 0 代表 水, 1 陆地, 2 遍历过的陆地
        int count = 0;
        for(int i=0; i < grid.length; i++){
            for(int j = 0; j < grid[0].length; j++){
                if(grid[i][j] == '1'){
                    count ++;
                    dfs(grid, i, j);
                }
            }
        }
        return count;
    }

    public void dfs(char[][] grid, int r, int c){
        if(!inArea(grid, r, c)){
            return;
        }
        if(grid[r][c] != '1'){
            return;
        }
        grid[r][c] = '2';
        dfs(grid, r-1, c);
        dfs(grid, r+1, c);
        dfs(grid, r, c-1);
        dfs(grid, r, c+1);
    }

    public boolean inArea(char[][] grid, int r, int c){
        return r>=0 && r < grid.length && c >= 0 && c < grid[0].length;
    }
}

---

Leetcode 463. 岛屿的周长

题目链接

题目说明

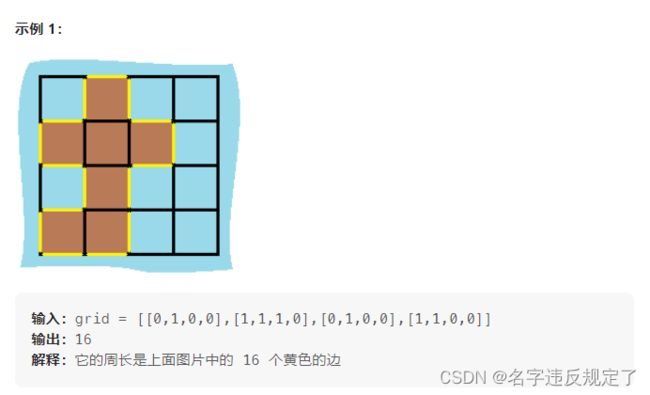
给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

代码说明

dfs 返回int,
如果碰到水或者出界了, 返回1, 说明这是一个周长
如果碰到2, 说明已经计算过了, 直接返回0
最后将所有的四周的dfs结果加起来

class Solution {
    public int islandPerimeter(int[][] grid) {
        for(int i = 0; i < grid.length; i++){
            for(int j = 0 ; j < grid[0].length; j++){
                if(grid[i][j] == 1){
                    return dfs(grid, i, j);
                }
            }
        }
        return 0;
    }

      public int dfs(int[][] grid, int r, int c){
        if(!inArea(grid, r, c)){
            return 1;
        }
        if(grid[r][c] == 0){
            return 1;
        }
          if(grid[r][c] == 2){
            return 0;
        }
        grid[r][c] = 2;
        return dfs(grid, r-1, c) + dfs(grid, r+1, c) +
        dfs(grid, r, c-1) + dfs(grid, r, c+1);
    }

    public boolean inArea(int[][] grid, int r, int c){
        return r>=0 && r < grid.length && c >= 0 && c < grid[0].length;
    }
}

---

Leetcode 695. 岛屿的最大面积

题目链接

题目说明

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

代码说明

先求出每个岛屿的面积, 在选择最大的那个.

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int maxArea = 0;
        for(int i = 0; i < grid.length; i++){
            for(int j = 0; j < grid[0].length; j++){
                maxArea = Math.max(maxArea, dfs(grid, i, j));
            }
        }
        return maxArea;

    }
    public int dfs(int[][] grid, int r, int c){
        if(!inArea(grid, r, c)){
            return 0;
        }
        if(grid[r][c] != 1){
            return 0;
        }

        grid[r][c] = 2;
        return 1 + dfs(grid, r-1, c) + dfs(grid, r+1, c) +
        dfs(grid, r, c-1) + dfs(grid, r, c+1);
    }

    public boolean inArea(int[][] grid, int r, int c){
        return r>=0 && r < grid.length && c >= 0 && c < grid[0].length;
    }
}

---

Leetcode 1905. 统计子岛屿

题目链接

题目说明

给你两个 m x n 的二进制矩阵 grid1 和 grid2 ，它们只包含 0 （表示水域）和 1 （表示陆地）。一个 岛屿 是由 四个方向 （水平或者竖直）上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。

如果 grid2 的一个岛屿，被 grid1 的一个岛屿 完全 包含，也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含，那么我们称 grid2 中的这个岛屿为 子岛屿 。

请你返回 grid2 中 子岛屿 的 数目 。

代码说明

这个题目就比之前的要稍微复杂一下
方法一, 先找出那些不属于子岛的岛屿, 将其淹没掉, 然后计算剩下的grid2中的岛屿的数量

class Solution {
    public int countSubIslands(int[][] grid1, int[][] grid2) {
        int m = grid1.length, n = grid1[0].length;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid1[i][j] == 0 && grid2[i][j] == 1){
                    dfs(grid2, i, j); //淹没不是子岛的部分
                }
            }
        }
        int count = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid2[i][j] == 1){
                    count++;
                    dfs(grid2, i, j); 
                }
            }
        }
        return count;
    }

    public void dfs(int[][] grid, int i, int j){
        if(i < 0 || j < 0 || i >= grid.length || j >= grid[0].length){
            return;
        }

        if(grid[i][j] != 1){
            return;
        }
        grid[i][j] = 0; // 淹掉
        dfs(grid, i+1, j);
        dfs(grid, i-1, j);
        dfs(grid, i, j+1);
        dfs(grid, i, j-1);
    }
}

方法二, 一边判断一边遍历, 复制大神的写法

class Solution {
    public int countSubIslands(int[][] grid1, int[][] grid) {
        int n = grid.length, m = grid[0].length;
        int res = 0;
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                if(grid[i][j] == 1){
                    if(dfs(grid1, grid, i, j)){
                        res++;
                    }
                }
            }
        }

        return res;
    }

    public boolean dfs(int[][] grid1, int[][] grid, int i, int j){
        int n = grid.length, m = grid[0].length;

        if(i < 0 || j < 0 || i >= n || j >= m){
            return true;
        }
        if(grid[i][j] == 0){
            return true;
        }

        grid[i][j] = 0;
        boolean flag = true;
        if(grid1[i][j] == 0){ 
            // ⭐这里不能直接返回false，否则后面的dfs递归代码就不再执行了
            flag = false;
        }

        // ⭐必须要这样每一个都记录，来保证每一个dfs递归都执行
        // 不能直接reutrn dfs() && dfs() && dfs() && dfs()
        // 否则遇到第一个false，后面的就不再执行了
        boolean flag1 = dfs(grid1, grid, i - 1, j);
        boolean flag2 = dfs(grid1, grid, i + 1, j);
        boolean flag3 = dfs(grid1, grid, i, j - 1);
        boolean flag4 = dfs(grid1, grid, i, j + 1);
        
        return  flag && flag1 && flag2 && flag3 && flag4;
    }
}

---

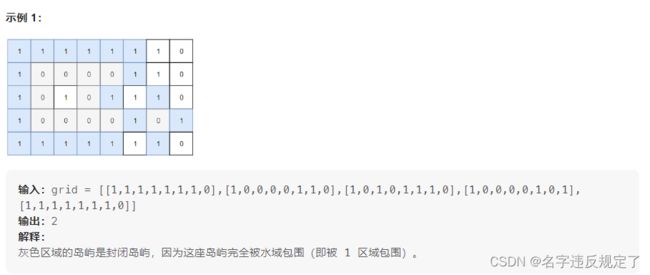
Leetcode 1254. 统计封闭岛屿的数目

二维矩阵 grid 由 0 （土地）和 1 （水）组成。岛是由最大的4个方向连通的 0 组成的群，封闭岛是一个 完全 由1包围（左、上、右、下）的岛。

请返回 封闭岛屿 的数目。

题目链接

题目说明

二维矩阵 grid 由 0 （土地）和 1 （水）组成。岛是由最大的4个方向连通的 0 组成的群，封闭岛是一个 完全 由1包围（左、上、右、下）的岛。

请返回 封闭岛屿 的数目。

代码说明

和上面的题目类似, 也是需要一边判断一边比较, 不能立即返回, 要所有的遍历完之后再返回结果

class Solution {
    public int closedIsland(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int res =0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 0 && dfs(grid, i, j)){
                    res++;
                }
            }
        }
        return res;
    }

    public boolean dfs(int[][] grid, int i, int j){
        int m = grid.length, n = grid[0].length;
        if(i < 0 || j < 0 || i >= m || j >= n){
            return false;
        }
        if(grid[i][j] == 1){
            return true;
        }
        grid[i][j] = 1;

        boolean flag1= dfs(grid, i-1, j);
        boolean flag2= dfs(grid, i+1, j);
        boolean flag3= dfs(grid, i, j-1);
        boolean flag4= dfs(grid, i, j+1);
        return flag1 && flag2 && flag3 && flag4;
    }
}

---

Leetcode 417. 太平洋大西洋水流问题

题目链接

题目说明

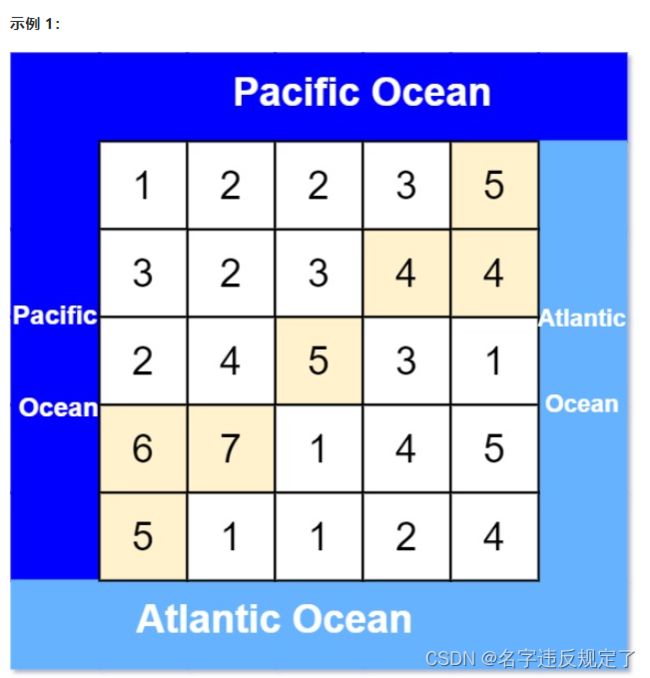
有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

代码说明

这个题目就需要逆向思维了.
解题的思路是, 先从两边出发, 找到从太平洋可以流过的土地, 再找到大西洋可流过的土地, 最后找重合的点.

如果当前的点小与上一个点的高度, 那就不能流过去

class Solution {
    int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    int[][] heights;
    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        List<List<Integer>> res = new ArrayList<>();
        this.heights = heights;
        int m = heights.length, n = heights[0].length;
        boolean[][] atlantic = new boolean[m][n];
        boolean[][] pacific = new boolean[m][n];

        for(int i = 0; i < m; i ++){
            dfs(i, 0, atlantic, Integer.MIN_VALUE);
            dfs(i, n-1, pacific, Integer.MIN_VALUE);
        }

        for(int i = 0; i < n; i++){
            dfs(0, i, atlantic, Integer.MIN_VALUE);
            dfs(m-1, i, pacific, Integer.MIN_VALUE);
        }

        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(atlantic[i][j] && pacific[i][j]){
                    res.add(Arrays.asList(i, j));
                }
            }
        }
        return res;

    }

    public void dfs(int row, int col, boolean[][] ocean, int prevH){
        if(row < 0 || row >= heights.length || col < 0 || col >= heights[0].length){
            return;
        }

        if(heights[row][col] < prevH || ocean[row][col]){
            return;
        }

        ocean[row][col] = true; // 该点可到达海洋
        prevH = heights[row][col];
        for(int[] dir : dirs ){
            dfs(row + dir[0], col+dir[1], ocean, prevH);
        }
    }


}