回溯、贪心、动态规划— 52.N皇后II 649.Dota2 参议院 1221.分割平衡字符串 5.最长回文子串 132.分割回文串II 673.最长递增子序列的个数 300.最长递增子序列C++实现
文章目录
- 52. N皇后II
- 649. Dota2 参议院
- 1221. 分割平衡字符串
- 647. 回文子串
- 5. 最长回文子串
-
- 动态规划
- 双指针
- 132. 分割回文串 II
- 673.最长递增子序列的个数
- 300.最长递增子序列
52. N皇后II
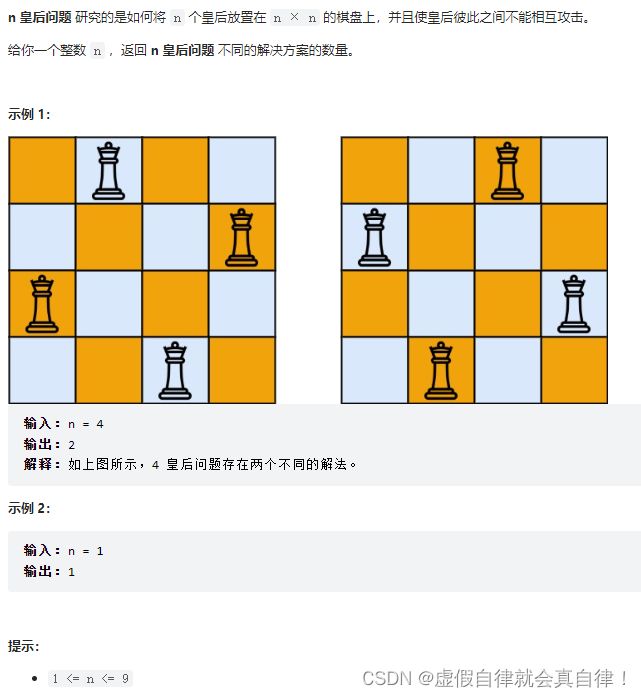
和51. N皇后一样,51题是输出所有结果集合,52题是输出所有结果的数量。
class Solution {
public:
int totalNQueens(int n) {
//1.构造棋盘 n*n棋盘 初始化为.
std::vector<std::string> chessboard(n, std::string(n, '.'));
dfs(0, n, chessboard);
return count;
}
private:
int count = 0;//记录所有解法数量
//验证皇后位置是否合法
bool isValid(int row, int col, int n, vector<string>& chessboard)
{
int count = 0;
//验证列 剪枝
for(int i=0; i<row; i++)
{
if(chessboard[i][col] == 'Q') return false;
}
//45° 右上角
for(int i=row-1, j=col-1; i>=0 && j>=0; i--, j--)
{
if(chessboard[i][j] == 'Q') return false;
}
//135° 左上角
for(int i=row-1, j=col+1; i>=0 && j<n; i--, j++)
{
if(chessboard[i][j] == 'Q') return false;
}
return true;
}
void dfs(int row, int n, vector<string>& chessboard)
{
//row记录当前遍历到棋盘的第几层
if(row == n)
{
count++;
return;
}
for(int col=0; col<n; col++)
{
//验证位置是否合法 合法则放置皇后 递归 回溯
if(isValid(row, col, n, chessboard))
{
chessboard[row][col] = 'Q';
dfs(row+1, n, chessboard);
chessboard[row][col] = '.';
}
}
}
};
649. Dota2 参议院

题意描述

贪心策略

用一个变量记录当前参议员之前有几个敌对对手了,进而判断自己是否被消灭了
class Solution {
public:
string predictPartyVictory(string senate) {
// R = true表示本轮循环结束后,字符串里依然有R, D同理
bool R = true, D = true;
// 当flag大于0时,R在D前出现,R可以消灭D。当flag小于0时,D在R前出现,D可以消灭R
int flag = 0;
// 一旦R或者D为false,就结束循环,说明本轮结束后只剩下R或者D了
while(R && D)
{
R = false;
D = false;
for(int i=0; i<senate.size(); i++)
{
if(senate[i] == 'R')//当前是R
{
//D在R前面 R被消灭 R此时为false
if(flag < 0) senate[i] = 0;
else R = true;//R没有被消灭
flag++;//R前面没有D了
}
if(senate[i] == 'D')
{
//R在D前面 D被消灭 D此时为false
if(flag > 0) senate[i] = 0;
else D = true;
flag--;
}
}
}
//循环结束后 如果有R剩下就是R胜利
return R == true ? "Radiant" : "Dire";
}
};
1221. 分割平衡字符串
局部最优:从前向后遍历,只要遇到平衡子串LR就统计。全局最优:统计了最多的平衡子串。
class Solution {
public:
int balancedStringSplit(string s) {
//count恰好等于0 说明遇到一个平衡子串 result+1
int count = 0;//遇到R +1;遇到L -1
int result = 0;
for(int i=0; i<s.size(); i++)
{
if(s[i] == 'R') count++;
else count--;
if(count == 0) result++;
}
return result;
}
};
647. 回文子串
- dp[i][j]:区间[i, j]的字符串是回文子串则为true,否则为false
- 遍历的顺序是从下到上,从左到右,dp[i][j]来源于dp[i+1][j-1]
- 分情况讨论:s[i] ≠ s[j],dp[i][j]=false;s[i] = s[j],有三种情况
- 情况一,下标i 与 j相同,同一个字符例如a,true
- 情况二,下标i 与 j相差为1,例如aa,true
- 情况三,下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]相同了,再看aba是否为回文也就是看区间[i+1, j-1],即看dp[i + 1][j - 1]是否为true。
class Solution {
public:
int countSubstrings(string s) {
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
int result = 0;//统计回文子串的数量
//从上到下 左到右遍历
for(int i=s.size(); i>=0; i--)
{
for(int j=i; j<s.size(); j++)
{
if(s[i] == s[j])
{
//情况1和2 一个字符或者两个字符 a或者aa
if(j - i <= 1)
{
dp[i][j] = true;
result++;
}
//情况3 dp[i+1][j-1]为true
else if(dp[i+1][j-1])
{
dp[i][j] = true;
result++;
}
}
}
}
return result;
}
};
5. 最长回文子串
动态规划
- dp[i][j]:区间[i, j]的字符串是回文子串则为true,否则为false
- 遍历的顺序是从下到上,从左到右,dp[i][j]来源于dp[i+1][j-1]
- 分情况讨论:s[i] ≠ s[j],dp[i][j]=false;s[i] = s[j],有三种情况
- 情况一,下标i 与 j相同,同一个字符例如a,true
- 情况二,下标i 与 j相差为1,例如aa,true
- 情况三,下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]相同了,再看aba是否为回文也就是看区间[i+1, j-1],即看dp[i + 1][j - 1]是否为true。
和题647不同的是,如果找到最长的回文子串,要保存左右边界
class Solution {
public:
int left = 0;
int right = 0;
int maxlen = 0;
string longestPalindrome(string s) {
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
for(int i=s.size()-1; i>=0; i--)
{
for(int j=i; j<s.size(); j++)
{
if(s[i] == s[j])
{
if(j - i <= 1) dp[i][j] = true;
else if(dp[i+1][j-1]) dp[i][j] = true;
}
if(dp[i][j] && (j - i + 1 > maxlen))
{
left = i;
right = j;
maxlen = j - i + 1;
}
}
}
return s.substr(left, right - left + 1);//输入babad 输出aba
};
双指针
首先确定回文串,就是找中心然后想两边扩散看是不是对称的。在遍历中心点的时候,要注意中心点有两种情况:一个元素可以作为中心点,两个元素也可以作为中心点。
class Solution {
public:
int left = 0;
int right = 0;
int maxlen = 0;
string longestPalindrome(string s) {
//2.双指针
//找到中心 然后两边扩散 i为中心 i i+1为中心
for(int i=0; i<s.size(); i++)
{
extend(s, i, i, s.size());
extend(s, i, i+1, s.size());
}
return s.substr(left, maxlen);//输入babad 输出bab
}
void extend(string& s, int i, int j, int n)
{
//i j在有效范围内 且字符相同
while(i>=0 && j<n && s[i]==s[j])
{
//找到更长的回文子串
if(j - i + 1 > maxlen)
{
left = i;
right = j;
maxlen = j - i + 1;
}
i--;
j++;
}
}
};
132. 分割回文串 II
这道题分为两部分,第一个是判断区间[i, j]是否为回文子串,第二个是分割回文子串。
判断回文子串:题647、题5
分割回文子串:
- dp[i]:范围是[0, i]的回文子串,最少分割次数是dp[i]。
- 递推公式为:
dp[i] = min(dp[i], dp[j] + 1);
如果要对长度为[0, i]的子串进行分割,分割点为j。分割后回文子串的区间[j + 1, i]。根据dp[i]的定义,[0, j]区间的最小切割数量是dp[j],那么dp[i] = dp[j] + 1。要找到最少分割次数,遍历时要取最小的dp[i],所以最后递推公式为:dp[i] = min(dp[i], dp[j] + 1);,min是为了取最小的dp[i]。 - 初始化:dp[0] = 0;非0下标dp[i]初始化为一个最大数,推导过程中再更新,或者非0下标dp[i]初始化为 i 本身
dp[i] = min(dp[i], dp[j] + 1);,所以 i 的遍历在外层for循环,j 的遍历在内层for循环。
class Solution {
public:
int minCut(string s) {
//1.判断是否为回文子串
vector<vector<bool>> isPalinddromic(s.size(), vector<bool>(s.size(), false));
for(int i=s.size()-1; i>=0; i--)
{
for(int j=i; j<s.size(); j++)
{
if(s[i]==s[j] && (j - i <= 1 || isPalinddromic[i+1][j-1])) isPalinddromic[i][j] = true;
}
}
//2.切割回文子串
vector<int> dp(s.size(), 0);
//两种初始化
for(int i=0; i<s.size(); i++) dp[i] = i;
//for(int i=1; i
//分割
for(int i=1; i<s.size(); i++)
{
//判断[0, i]是否为回文串,是则dp[i] = 0,i更新
if(isPalinddromic[0][i])
{
//是回文串 不用分割 分割次数为0
dp[i] = 0;
continue;
}
//分割[0, i] 分割点j 分割后的子串区间是[j+1, i]
for(int j=0; j<i; j++)
{
//[j+1, i]是回文串,dp[i]分割次数=dp[j]+1
if(isPalinddromic[j+1][i]) dp[i] = min(dp[i], dp[j] + 1);
}
}
return dp[s.size() - 1];//返回整体分割 的最小次数
}
};
673.最长递增子序列的个数
- 确定dp数组(dp table)以及下标的含义:
- dp[i]:i之前(包括i)最长递增子序列的长度为dp[i];
- count[i]:以nums[i]为结尾的字符串,最长递增子序列的个数为count[i]
- 确定递推公式
- dp[i]的更新,dp[i] 取 dp[j] + 1的最大值,j 小于 i,即
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1); - count[i]的更新:
- 如果nums[i] > nums[j],在[0, i-1]的范围内找到了j,使得dp[j] + 1 > dp[i],说明找到了一个更长的递增子序列。那么以i为结尾的子串的最长递增子序列的个数 更新为 以j为结尾的子串的最长递增子序列的个数,即:count[i] = count[j]。
- 如果nums[i] > nums[j],在[0, i-1]的范围内找到了j,使得dp[j] + 1 == dp[i],说明找到了两个相同长度的递增子序列。那么以i为结尾的子串的最长递增子序列的个数 就应该加上以j为结尾的子串的最长递增子序列的个数,即:count[i] += count[j];
- 最后记录题目要求的递增序列的长度的个数
- dp数组如何初始化
- count[i]记录了最长递增子序列的个数,最少个数是1,count[i]初始为1。
- dp[i]记录了最长递增序列的长度,最小长度是1,dp[i]初始为1。
-
确定遍历顺序
dp[i] 是由0到 i-1 各个位置的最长升序子序列 推导而来,遍历i是从前向后遍历。j 在0到i-1,遍历i的循环里外层,遍历j则在内层。
最后还要再遍历一遍dp[i],把最长递增序列长度对应的count[i]累计下来就是结果了,count只是记录了位置i之前的结果。
class Solution {
public:
int findNumberOfLIS(vector<int>& nums) {
if(nums.size() <= 1) return nums.size();
vector<int> dp(nums.size(), 1);//0-i递增子序列最长长度
vector<int> count(nums.size(), 1);//0-i最长递增子序列的个数
int maxcount = 0;
for(int i=1; i<nums.size(); i++)
{
for(int j=0; j<i; j++)
{
if(nums[i] > nums[j])//递增序列
{
if(dp[j]+1 > dp[i])//[0, i-1]有更长的递增子序列
{
dp[i] = dp[j] + 1;
count[i] = count[j];
}
else if(dp[j]+1 == dp[i])
{
count[i] += count[j];
}
}
if(dp[i] > maxcount) maxcount = dp[i];
}
}
//求整个数组中 都是最长递增子序列子串的总个数
int result = 0;
//for(int c : count) result += c;
for(int i=0; i<nums.size(); i++)
{
if(maxcount == dp[i]) result += count[i];
}
return result;
}
};
300.最长递增子序列
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
if(nums.size() <= 1) return nums.size();
int result = 0;
vector<int> dp(nums.size(), 1);
for(int i=1; i<nums.size(); i++)
{
for(int j=0; j<i; j++)
{
if(nums[i] > nums[j] && (dp[j]+1 > dp[i]))
{
dp[i] = dp[j] + 1;
}
if(dp[i] > result) result = dp[i];
}
}
return result;
}
};