二叉树创建并输入输出（链式结构）

      要进行二叉树的创建以及输入输出首先我们都应该遍历到二叉树各个结点才能进行相应的操作，二叉树的遍历方法一共有3种：

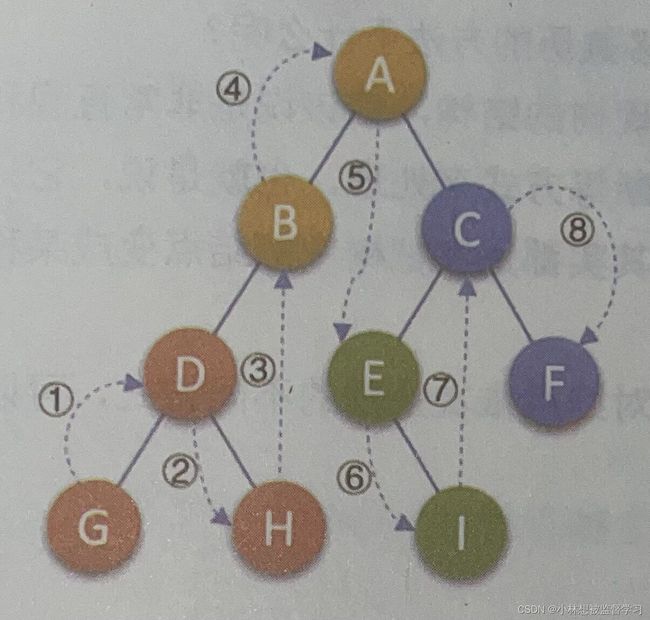
   1.前序遍历（先结点，再左子树，再右子树）

 

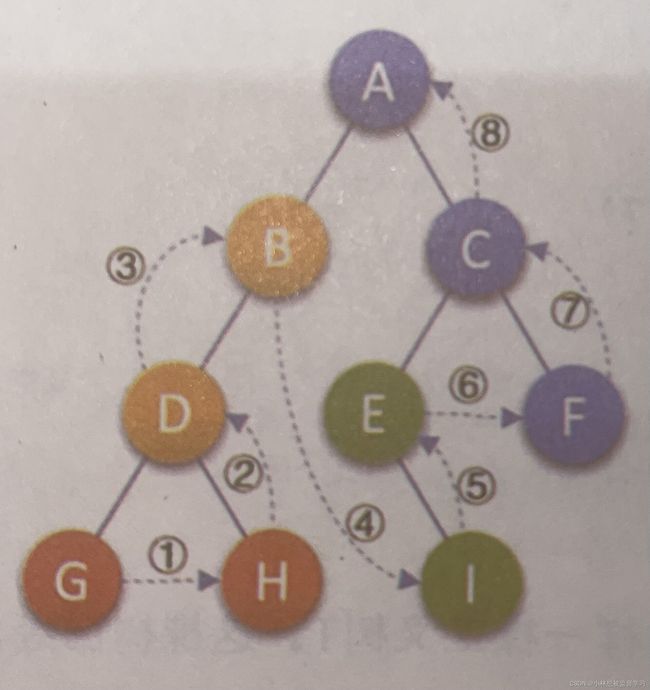
   2.中序遍历（先左子树，再结点，再右子树）

 

   3.后序遍历（先左子树，再右子树，再结点）

       代码展示：

    首先肯定要进行二叉树结构的定义：

//二叉树的结构
typedef struct My_BitreeNode
{
	//数据域
	ElemType data;
	//左子树指针
	My_BitreeNode* lchild;
	//右子树指针
	My_BitreeNode* rchild;
}My_BitreeNode,*My_BitreePointer;

二叉树由于有左子树和右子树所以要有两个指向下级的指针。

  1.向二叉树输入数据（前序遍历）

//向二叉树输入数据（前序遍历）
void CreateBiTree_front(My_BitreePointer&T)
{
	//用来接受用户输入的数据
	ElemType ch;
	cin >> ch;
	//规定空结点输入‘#’
	if (ch == '#')
	{
		//空结点没有创建的必要，将此时指向空结点的指针指向空
		T = NULL;
	}
	//不是空结点，要创建具体结点
	else
	{
		T = new(My_BitreeNode);
		//判断空间是否创建成功
		if (T == NULL)
			exit(0);
		//生成根结点
		T->data = ch;
		//递归左子树
		CreateBiTree_front(T->lchild);
		//递归右子树
		CreateBiTree_front(T->rchild);
	}
}

      我们规定了输入‘ # ’就说明遍历到的该结点是不存在的不需要输入数据

      ps：我们在遍历二叉树是采用了递归的方法，而递归函数的编写要特别注意3个点：

1.确定递归的参数和返回值

       递归的参数可以不用一开始就设定好，可以在编写程序过程中看需要传入什么参数，而返回值一般都是void，因为我们把结果直接放在参数里了。

2.确定终止条件

      编写递归函数要是不确定好终止条件就经常会导致栈溢出等问题，我们遍历二叉树的终止条件就是在遍历到空指针后就说明无法再往下遍历，于是return回上一个结点。

3.确定单层递归的逻辑

      我们当前在编写的是前序遍历，所以我们要先处理结点，然后在去遍历左子树，最后遍历右子树。

2.前序输出

//前序输出
void PrintBitree_front(My_BitreePointer& T)
{
	if (!T)
	{
		return;
	}
	//输出结点
	cout << T->data << " ";
	//递归左子树
	PrintBitree_front(T->lchild);
	//递归右子树
	PrintBitree_front(T->rchild);
}

   与上文前序输出的遍历过程完全相同只是对结点的处理不同，一个像结点中输入数据，一个输出结点中的数据

3.向二叉树输入数据(中序遍历)

//向二叉树输入数据(中序遍历)
void CreateBiTree_middle(My_BitreePointer& T)
{
	ElemType ch;
	cin >> ch;
	if (ch == '#')
	{
		T = NULL;
	}
	else
	{
		T = new(My_BitreeNode);
		//判断空间是否创建成功
		if (T == NULL)
			exit(0);
		//递归左子树
		CreateBiTree_middle(T->lchild);
		//生成根结点
		T->data = ch;
		//递归右子树
		CreateBiTree_middle(T->rchild);
	}
}

   仔细观察我们便会发现这与前序遍历二叉树输入数据基本相同，就是改变了递归函数和生成结点操作的顺序，因为中序遍历是按照左子树，结点，右子树的方式遍历的，所以我们要先递归左子树，再向结点输入数据，再递归右子树。仅仅更换了单层递归的逻辑。

   同理我们也可以轻易的知道后序遍历的代码，先递归左子树，再递归右子树，再处理结点

4.中序输出

//中序输出
void PrintBitree_middle(My_BitreePointer& T)
{
	if (T == NULL)
		return;
	else
	{
		//递归左子树
		PrintBitree_middle(T->lchild);
		//输出结点
		cout << T->data << " ";
		//递归右子树
		PrintBitree_middle(T->rchild);
	}
}

   特别注意，我们在输入的时候一定要补齐二叉树，输入足够多的‘ # ’要不然二叉树是无法创建的。