【数据挖掘】将NLP技术引入到股市分析
一、说明
在交易中实施的机器学习模型通常根据历史股票价格和其他定量数据进行训练,以预测未来的股票价格。但是,自然语言处理(NLP)使我们能够分析财务文档,例如10-k表格,以预测股票走势。
二、对自然语言处理解释
自然语言处理是人工智能的一个分支,涉及教计算机阅读语言并从语言中获取含义。由于语言是如此复杂,计算机必须经过一系列步骤才能理解文本。以下是典型 NLP 管道中出现的步骤的快速说明。
- 句子分割 文本文档被分割
成单独的句子。 - 标记化
一旦文档被分解成句子,我们进一步将句子分成单独的单词。每个单词称为一个标记,因此称为标记化。 - 词性标记
我们将每个标记及其周围的几个单词输入到预先训练的词性分类模型中,以接收标记的词性作为输出。 - 词形还原
词通常以不同的形式出现,同时指代相同的对象/动作。为了防止计算机将单词的不同形式视为不同的单词,我们执行词形还原,即将单词的各种屈折组合在一起以将它们分析为单个项目的过程,由单词的引理(单词在字典中的出现方式)标识。 - 停用词 诸如“and”、“the”和“a”等极其常见的单词不提供任何值,因此我们将它们标识为停用词
,以将其从对文本执行的任何分析中排除。 - 依赖关系分析 为句子分配句法结构,并通过将单词提供给依赖关系分析
器来理解句子中的单词之间的关系。 - 名词短语 将句子中的名词短语
组合在一起可以帮助简化我们不关心形容词的情况的句子。 - 命名实体识别
命名实体识别模型可以标记人员姓名、
公司名称和地理位置等对象。 - 共指解决
由于 NLP 模型分析单个句子,因此它们会被代词引用其他句子中的名词所混淆。为了解决这个问题,我们采用共指解析来跟踪句子中的代词以避免混淆。
有关 NLP 的更深入描述:请阅读此内容
完成这些步骤后,我们的文本就可以进行分析了。现在我们更好地理解了NLP,让我们来看看我的项目代码(来自Udacity的AI交易课程的项目5)。单击此处查看完整的 Github 存储库
三、NLP的数据导入/下载
首先,我们进行必要的进口;project_helper包含各种实用程序和图形函数。
import nltk
import numpy as np
import pandas as pd
import pickle
import pprint
import project_helper
from tqdm import tqdm然后我们下载用于删除停用词的停用词语料库和用于词形还原的词网语料库。
nltk.download('stopwords')
nltk.download('wordnet')四、获取 10-ks数据
10-K 文档包括公司历史、组织结构、高管薪酬、股权、子公司和经审计的财务报表等信息。要查找 10-k 文档,我们使用每个公司的唯一 CIK(中央索引键)。
cik_lookup = {
'AMZN': '0001018724',
'BMY': '0000014272',
'CNP': '0001130310',
'CVX': '0000093410',
'FL': '0000850209',
'FRT': '0000034903',
'HON': '0000773840'}现在,我们从 SEC 中提取已提交的 10-k 列表,并以亚马逊数据为例显示。
sec_api = project_helper.SecAPI()
from bs4 import BeautifulSoup
def get_sec_data(cik, doc_type, start=0, count=60):
rss_url = 'https://www.sec.gov/cgi-bin/browse-edgar?action=getcompany' \
'&CIK={}&type={}&start={}&count={}&owner=exclude&output=atom' \
.format(cik, doc_type, start, count)
sec_data = sec_api.get(rss_url)
feed = BeautifulSoup(sec_data.encode('ascii'), 'xml').feed
entries = [
(
entry.content.find('filing-href').getText(),
entry.content.find('filing-type').getText(),
entry.content.find('filing-date').getText())
for entry in feed.find_all('entry', recursive=False)]
return entries
example_ticker = 'AMZN'
sec_data = {}
for ticker, cik in cik_lookup.items():
sec_data[ticker] = get_sec_data(cik, '10-K')
pprint.pprint(sec_data[example_ticker][:5])我们收到一个 url 列表,这些网址指向包含与每个填充相关的元数据的文件。元数据与我们无关,因此我们通过用填充 URL 替换 url 来提取填充。让我们使用 tqdm 查看下载进度并查看示例文档。
raw_fillings_by_ticker = {}
for ticker, data in sec_data.items():
raw_fillings_by_ticker[ticker] = {}
for index_url, file_type, file_date in tqdm(data, desc='Downloading {} Fillings'.format(ticker), unit='filling'):
if (file_type == '10-K'):
file_url = index_url.replace('-index.htm', '.txt').replace('.txtl', '.txt')
raw_fillings_by_ticker[ticker][file_date] = sec_api.get(file_url)
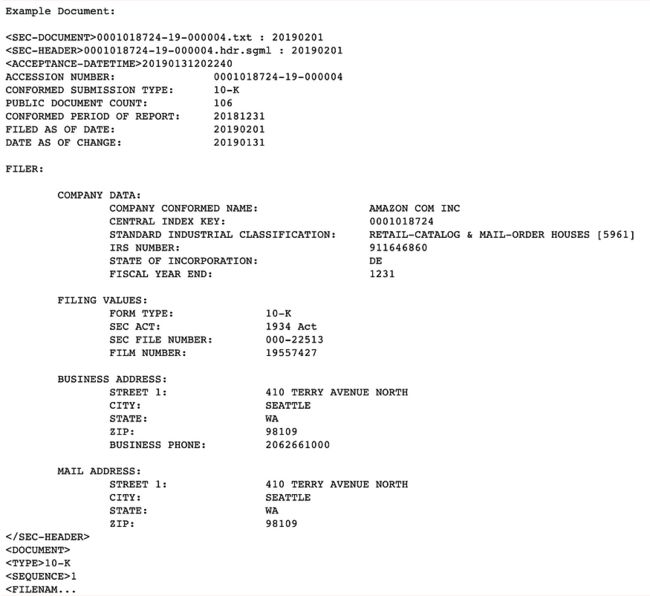
print('Example Document:\n\n{}...'.format(next(iter(raw_fillings_by_ticker[example_ticker].values()))[:1000])) 将下载的文件分解为其关联的文档,这些文档在填充物中被分割开来,标签
import re
def get_documents(text):
extracted_docs = []
doc_start_pattern = re.compile(r'')
doc_end_pattern = re.compile(r' ')
doc_start_is = [x.end() for x in doc_start_pattern.finditer(text)]
doc_end_is = [x.start() for x in doc_end_pattern.finditer(text)]
for doc_start_i, doc_end_i in zip(doc_start_is, doc_end_is):
extracted_docs.append(text[doc_start_i:doc_end_i])
return extracted_docs
filling_documents_by_ticker = {}
for ticker, raw_fillings in raw_fillings_by_ticker.items():
filling_documents_by_ticker[ticker] = {}
for file_date, filling in tqdm(raw_fillings.items(), desc='Getting Documents from {} Fillings'.format(ticker), unit='filling'):
filling_documents_by_ticker[ticker][file_date] = get_documents(filling)
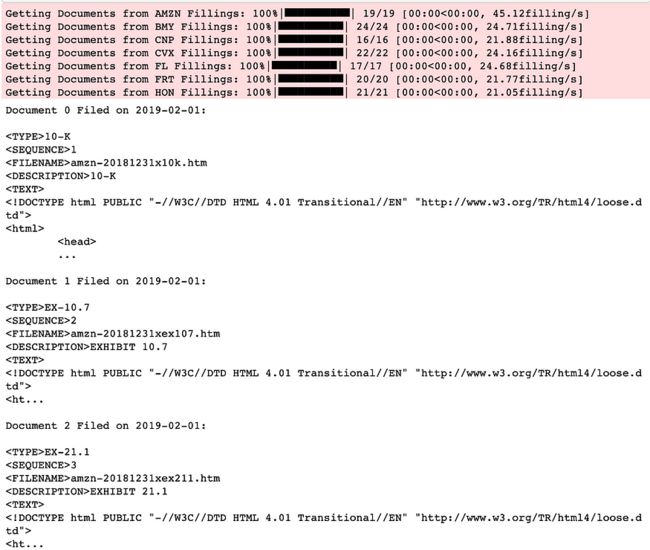
print('\n\n'.join([
'Document {} Filed on {}:\n{}...'.format(doc_i, file_date, doc[:200])
for file_date, docs in filling_documents_by_ticker[example_ticker].items()
for doc_i, doc in enumerate(docs)][:3]))定义 get_document_type 函数以返回给定的文档类型。
def get_document_type(doc):
type_pattern = re.compile(r'[^\n]+')
doc_type = type_pattern.findall(doc)[0][len(''):]
return doc_type.lower() 使用 get_document_type 功能从填充物中过滤掉非 10-k 文档。
ten_ks_by_ticker = {}
for ticker, filling_documents in filling_documents_by_ticker.items():
ten_ks_by_ticker[ticker] = []
for file_date, documents in filling_documents.items():
for document in documents:
if get_document_type(document) == '10-k':
ten_ks_by_ticker[ticker].append({
'cik': cik_lookup[ticker],
'file': document,
'file_date': file_date})
project_helper.print_ten_k_data(ten_ks_by_ticker[example_ticker][:5], ['cik', 'file', 'file_date'])五、预处理数据
删除 html 并将所有文本设置为小写以清理文档文本。
def remove_html_tags(text):
text = BeautifulSoup(text, 'html.parser').get_text()
return text
def clean_text(text):
text = text.lower()
text = remove_html_tags(text)
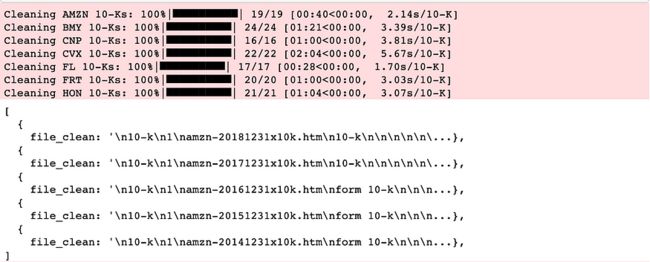
return text使用clean_text功能清理文档。
for ticker, ten_ks in ten_ks_by_ticker.items():
for ten_k in tqdm(ten_ks, desc='Cleaning {} 10-Ks'.format(ticker), unit='10-K'):
ten_k['file_clean'] = clean_text(ten_k['file'])
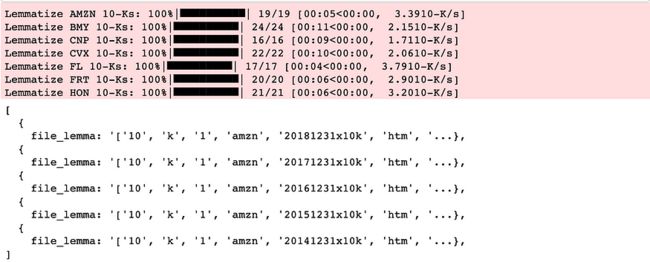
project_helper.print_ten_k_data(ten_ks_by_ticker[example_ticker][:5], ['file_clean'])现在我们对所有数据进行词形还原。
from nltk.stem import WordNetLemmatizer
from nltk.corpus import wordnet
def lemmatize_words(words):
lemmatized_words = [WordNetLemmatizer().lemmatize(word, 'v') for word in words]
return lemmatized_words
word_pattern = re.compile('\w+')
for ticker, ten_ks in ten_ks_by_ticker.items():
for ten_k in tqdm(ten_ks, desc='Lemmatize {} 10-Ks'.format(ticker), unit='10-K'):
ten_k['file_lemma'] = lemmatize_words(word_pattern.findall(ten_k['file_clean']))
project_helper.print_ten_k_data(ten_ks_by_ticker[example_ticker][:5], ['file_lemma'])删除停用词。
from nltk.corpus import stopwords
lemma_english_stopwords = lemmatize_words(stopwords.words('english'))
for ticker, ten_ks in ten_ks_by_ticker.items():
for ten_k in tqdm(ten_ks, desc='Remove Stop Words for {} 10-Ks'.format(ticker), unit='10-K'):
ten_k['file_lemma'] = [word for word in ten_k['file_lemma'] if word not in lemma_english_stopwords]
print('Stop Words Removed')六、10-ks 的情绪分析
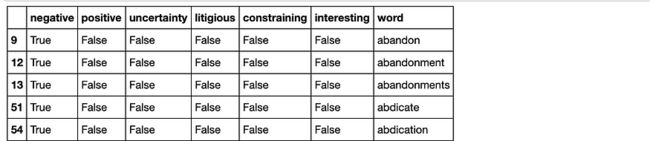
使用 Loughran-McDonald 情感词列表对 10-ks 执行情感分析(这是专门为文本分析相关的财务构建的)。
sentiments = ['negative', 'positive', 'uncertainty', 'litigious', 'constraining', 'interesting']
sentiment_df = pd.read_csv('loughran_mcdonald_master_dic_2018.csv')
sentiment_df.columns = [column.lower() for column in sentiment_df.columns] # Lowercase the columns for ease of use
# Remove unused information
sentiment_df = sentiment_df[sentiments + ['word']]
sentiment_df[sentiments] = sentiment_df[sentiments].astype(bool)
sentiment_df = sentiment_df[(sentiment_df[sentiments]).any(1)]
# Apply the same preprocessing to these words as the 10-k words
sentiment_df['word'] = lemmatize_words(sentiment_df['word'].str.lower())
sentiment_df = sentiment_df.drop_duplicates('word')
sentiment_df.head()使用情绪词列表从 10-k 文档生成单词的情绪包。单词袋计算每个文档中的情感单词数量。
from collections import defaultdict, Counter
from sklearn.feature_extraction.text import CountVectorizer
def get_bag_of_words(sentiment_words, docs):
vec = CountVectorizer(vocabulary=sentiment_words)
vectors = vec.fit_transform(docs)
words_list = vec.get_feature_names()
bag_of_words = np.zeros([len(docs), len(words_list)])
for i in range(len(docs)):
bag_of_words[i] = vectors[i].toarray()[0]
return bag_of_words.astype(int)
sentiment_bow_ten_ks = {}
for ticker, ten_ks in ten_ks_by_ticker.items():
lemma_docs = [' '.join(ten_k['file_lemma']) for ten_k in ten_ks]
sentiment_bow_ten_ks[ticker] = {
sentiment: get_bag_of_words(sentiment_df[sentiment_df[sentiment]]['word'], lemma_docs)
for sentiment in sentiments}
project_helper.print_ten_k_data([sentiment_bow_ten_ks[example_ticker]], sentiments)七、杰卡德相似性
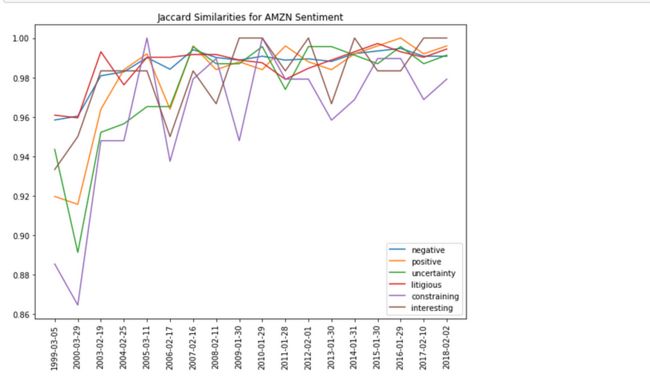
现在我们有了词袋,我们可以将其转换为布尔数组并计算 jaccard 相似性。杰卡德相似性定义为交集的大小除以两个集合的并集大小。例如,两个句子之间的jaccard相似性是两个句子之间的常用词数除以两个句子中唯一单词总数的总和。杰卡德相似性值越接近 1,集合就越相似。为了更容易理解我们的计算,我们绘制了杰卡德的相似性。
from sklearn.metrics import jaccard_similarity_score
def get_jaccard_similarity(bag_of_words_matrix):
jaccard_similarities = []
bag_of_words_matrix = np.array(bag_of_words_matrix, dtype=bool)
for i in range(len(bag_of_words_matrix)-1):
u = bag_of_words_matrix[i]
v = bag_of_words_matrix[i+1]
jaccard_similarities.append(jaccard_similarity_score(u,v))
return jaccard_similarities
# Get dates for the universe
file_dates = {
ticker: [ten_k['file_date'] for ten_k in ten_ks]
for ticker, ten_ks in ten_ks_by_ticker.items()}
jaccard_similarities = {
ticker: {
sentiment_name: get_jaccard_similarity(sentiment_values)
for sentiment_name, sentiment_values in ten_k_sentiments.items()}
for ticker, ten_k_sentiments in sentiment_bow_ten_ks.items()}
project_helper.plot_similarities(
[jaccard_similarities[example_ticker][sentiment] for sentiment in sentiments],
file_dates[example_ticker][1:],
'Jaccard Similarities for {} Sentiment'.format(example_ticker),
sentiments)八、TFIDF
从情绪词列表中,让我们从 10-k 文档生成情绪术语频率 – 反向文档频率 (TFIDF)。TFIDF 是一种信息检索技术,用于揭示单词/术语在所选文本集合中出现的频率。每个术语都分配有术语频率 (TF) 和反向文档频率 (IDF) 分数。这些分数的乘积称为该术语的 TFIDF 权重。TFIDF 权重越高表示术语越稀有,TFIDF 分数越低表示术语越常见。
from sklearn.feature_extraction.text import TfidfVectorizer
def get_tfidf(sentiment_words, docs):
vec = TfidfVectorizer(vocabulary=sentiment_words)
tfidf = vec.fit_transform(docs)
return tfidf.toarray()
sentiment_tfidf_ten_ks = {}
for ticker, ten_ks in ten_ks_by_ticker.items():
lemma_docs = [' '.join(ten_k['file_lemma']) for ten_k in ten_ks]
sentiment_tfidf_ten_ks[ticker] = {
sentiment: get_tfidf(sentiment_df[sentiment_df[sentiment]]['word'], lemma_docs)
for sentiment in sentiments}
project_helper.print_ten_k_data([sentiment_tfidf_ten_ks[example_ticker]], sentiments)九、余弦相似性
根据我们的 TFIDF 值,我们可以计算余弦相似性并将其绘制成随时间变化的图。与 jaccard 相似性类似,余弦相似性是用于确定文档相似程度的指标。余弦相似性通过测量投影在多维空间中的两个向量之间角度的余弦来计算相似性,而不考虑大小。对于文本分析,使用的两个向量通常是包含两个文档字数的数组。
from sklearn.metrics.pairwise import cosine_similarity
def get_cosine_similarity(tfidf_matrix):
cosine_similarities = []
for i in range(len(tfidf_matrix)-1):
cosine_similarities.append(cosine_similarity(tfidf_matrix[i].reshape(1, -1),tfidf_matrix[i+1].reshape(1, -1))[0,0])
return cosine_similarities
cosine_similarities = {
ticker: {
sentiment_name: get_cosine_similarity(sentiment_values)
for sentiment_name, sentiment_values in ten_k_sentiments.items()}
for ticker, ten_k_sentiments in sentiment_tfidf_ten_ks.items()}
project_helper.plot_similarities(
[cosine_similarities[example_ticker][sentiment] for sentiment in sentiments],
file_dates[example_ticker][1:],
'Cosine Similarities for {} Sentiment'.format(example_ticker),
sentiments)十、价格数据
现在,我们将通过将其与股票的年度定价进行比较来评估阿尔法因素。我们可以从QuoteMedia下载定价数据。
pricing = pd.read_csv('yr-quotemedia.csv', parse_dates=['date'])
pricing = pricing.pivot(index='date', columns='ticker', values='adj_close')
pricing十一、将数据转换为数据帧
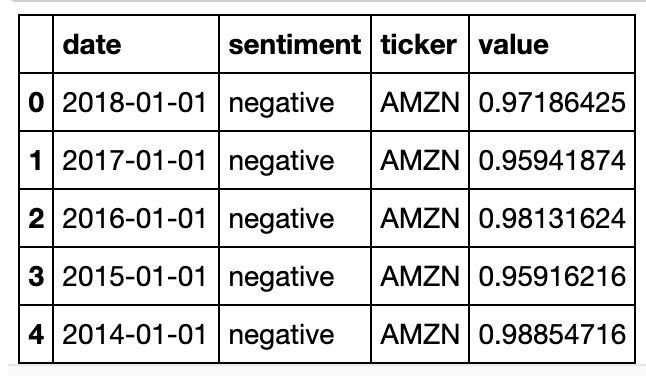
Alphalens是一个用于alpha因素性能分析的python库,它使用数据帧,因此我们必须将字典转换为数据帧。
cosine_similarities_df_dict = {'date': [], 'ticker': [], 'sentiment': [], 'value': []}
for ticker, ten_k_sentiments in cosine_similarities.items():
for sentiment_name, sentiment_values in ten_k_sentiments.items():
for sentiment_values, sentiment_value in enumerate(sentiment_values):
cosine_similarities_df_dict['ticker'].append(ticker)
cosine_similarities_df_dict['sentiment'].append(sentiment_name)
cosine_similarities_df_dict['value'].append(sentiment_value)
cosine_similarities_df_dict['date'].append(file_dates[ticker][1:][sentiment_values])
cosine_similarities_df = pd.DataFrame(cosine_similarities_df_dict)
cosine_similarities_df['date'] = pd.DatetimeIndex(cosine_similarities_df['date']).year
cosine_similarities_df['date'] = pd.to_datetime(cosine_similarities_df['date'], format='%Y')
cosine_similarities_df.head()在利用许多 alphalens 函数之前,我们需要对齐索引并将时间转换为 unix 时间戳。
import alphalens as al
factor_data = {}
skipped_sentiments = []
for sentiment in sentiments:
cs_df = cosine_similarities_df[(cosine_similarities_df['sentiment'] == sentiment)]
cs_df = cs_df.pivot(index='date', columns='ticker', values='value')
try:
data = al.utils.get_clean_factor_and_forward_returns(cs_df.stack(), pricing.loc[cs_df.index], quantiles=5, bins=None, periods=[1])
factor_data[sentiment] = data
except:
skipped_sentiments.append(sentiment)
if skipped_sentiments:
print('\nSkipped the following sentiments:\n{}'.format('\n'.join(skipped_sentiments)))
factor_data[sentiments[0]].head()我们还必须创建具有 unix 时间的因子数据帧,以便与 alphalen 的factor_rank_autocorrelation和mean_return_by_quantile函数兼容。
unixt_factor_data = {
factor: data.set_index(pd.MultiIndex.from_tuples(
[(x.timestamp(), y) for x, y in data.index.values],
names=['date', 'asset']))
for factor, data in factor_data.items()}十二、因子回报
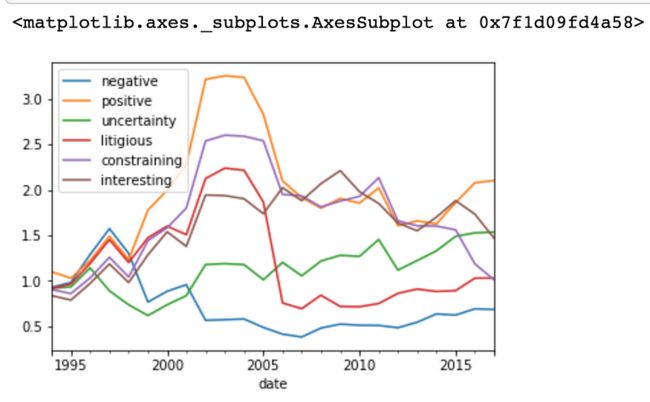
让我们来看看随时间推移的因子回报
ls_factor_returns = pd.DataFrame()
for factor_name, data in factor_data.items():
ls_factor_returns[factor_name] = al.performance.factor_returns(data).iloc[:, 0]
(1 + ls_factor_returns).cumprod().plot()正如预期的那样,表达积极情绪的 10-k 报告产生的收益最大,而包含负面情绪的 10-k 报告导致的最大损失。
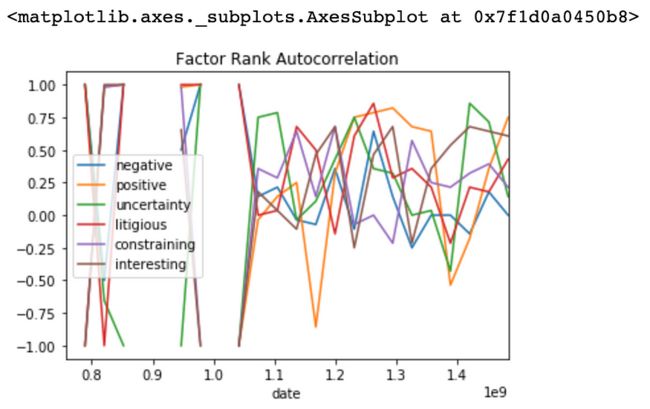
十三、营业额分析
使用因子秩自相关,我们可以分析alpha随时间推移的稳定性。我们希望阿尔法等级在不同时期保持相对相同。
ls_FRA = pd.DataFrame()
for factor, data in unixt_factor_data.items():
ls_FRA[factor] = al.performance.factor_rank_autocorrelation(data)
ls_FRA.plot(title="Factor Rank Autocorrelation")
十四、夏普比率
最后,让我们计算夏普比率,即平均回报减去无风险回报除以投资回报的标准差。
daily_annualization_factor = np.sqrt(252)
(daily_annualization_factor * ls_factor_returns.mean() / ls_factor_returns.std()).round(2)夏普比率为 1 被认为是可以接受的,2 的比率非常好,3 的比率非常好。正如预期的那样,我们可以看到积极情绪与高夏普比率相关,消极情绪与低夏普比率相关。其他情绪也与高夏普比率有关。然而,由于如此多的复杂因素影响股票价格,因此在现实世界中复制这些回报要困难得多。
参考和引用
[1] Udacity, Artificial Intelligence for Trading, Github
罗尚·阿杜苏米利