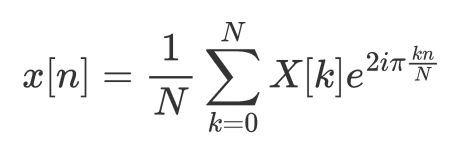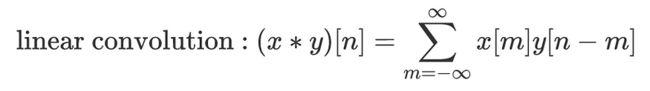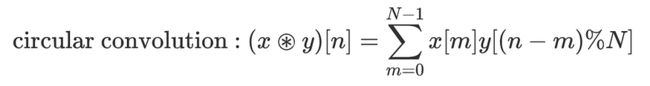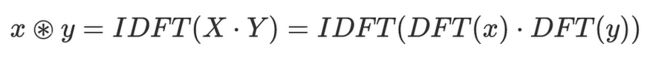【数据挖掘】时间序列的傅里叶变换:用numpy解释的快速卷积
一、说明
二、FFT的历史根源
傅里叶变换算法被认为是所有数学中最伟大的发现之一。法国数学家让-巴蒂斯特·约瑟夫·傅立叶在1822年的《Théorie analytique de la chaleur》一书中为调和分析奠定了基础。
法国数学家让·巴蒂斯特·约瑟夫·傅立叶(1768-1830 年)的雕刻肖像,19 世纪初。[来源:维基百科,图片来自公共领域]
这个奇妙的框架还为分析时间序列提供了很好的工具......这就是我们在这里的原因!
这篇文章是傅里叶变换系列文章的一部分。今天我们将讨论卷积以及傅里叶变换如何提供最快的方法。
三、离散傅里叶变换 (DFT) 的定义
让我们从基本定义开始。N 个元素的离散时间序列 x 的离散傅里叶变换为:
离散傅里叶变换 (DFT) 定义。存在其他定义,您只需要选择一个并坚持下去(由作者制作)
其中 k 表示 x 频谱的第 k 个频率。请注意,一些作者在该定义中添加了 1/N 的比例因子,但对这篇文章来说并不重要——总而言之,这只是一个定义问题并坚持下去。
然后是傅里叶逆变换(给定前向傅里叶变换的定义):
逆离散傅里叶变换,基于上述前向定义(由作者制作)。
话虽如此,傅里叶变换最重要的定理之一是一个空间中的卷积等价于另一个空间中的乘法。换句话说,乘积的傅里叶变换是相应傅里叶谱的卷积,卷积的傅里叶变换是相应傅里叶谱的乘积。
时域中的乘法对应于傅里叶域中的循环卷积(由作者制作)。
和
时域中的循环卷积对应于傅里叶域中的乘法(由作者制作)。
其中点表示标准乘积(乘法),圆圈星表示圆形卷积。
两个重要注意事项:
- 周期信号:傅里叶分析框架认为我们处理的信号是周期性的。换句话说,它们从负无穷大重复到无穷大。然而,使用有限的内存计算机处理此类信号并不总是实用的,因此我们只“玩”一个周期,我们将在后面看到。
- 循环卷积:卷积定理指出乘法等价于循环卷积,这与我们更习惯的线性卷积略有不同。正如我们将看到的,它并没有那么不同,也没有那么复杂。
四、循环卷积与线性卷积
如果您熟悉线性卷积(通常简称为“卷积”),那么您不会被循环卷积混淆。基本上,循环卷积只是卷积周期信号的方法。正如您可以猜到的,线性卷积仅对有限长度的信号有意义,这些信号的范围不是从负无穷大到无穷大。在我们的例子中,在傅里叶分析的上下文中,我们的信号是周期性的,因此不满足这个条件。我们不能谈论(线性)卷积。
然而,我们仍然可以直观地对周期信号进行线性卷积式操作:只需将周期信号卷积在一个周期长度上即可。这就是循环卷积的作用:它在一个周期跨度上卷积 2 个相同长度的周期信号。
为了进一步说服自己差异,请比较离散线性卷积和离散循环卷积的两个公式:
线性卷积方程:大多数时候在信号处理中,使用此公式,通过填充零(由作者制作)。
循环卷积 :这是处理周期信号时使用的卷积,如傅里叶分析(由作者制作)。
注意差异:
- 边界:线性卷积使用从负无穷大到正无穷大的样本 — 如前所述,在这种情况下,x 和 y 具有有限的能量,总和是有意义的。对于循环卷积,我们只需要在一个时间段内发生了什么,所以总和只跨越一个周期
- 循环索引 :在循环卷积中,我们使用长度为 N 的模运算“包装”y 的索引。这只是一种确保 y 被认为是周期为 N 的周期的方法:当我们想知道位置 k 处 y 的值时,我们只在位置 k%N 处使用 y 的值 — 因为 y 是 N 周期性的,我们得到正确的值。同样,这只是处理周期性无限长度样本序列的一种数学方法。
五、在 numpy 中的实现
Numpy为有限长度信号提供了很好的工具:这是一个好消息,因为正如我们刚刚看到的,我们的无限长度周期信号可以用一个周期来表示。
让我们创建一个简单的类来表示这些信号。我们添加了一个快速绘制数组的方法,以及“基本”数组前后的额外周期,以记住我们正在处理周期序列。
import numpy as np
import matplotlib.pyplot as plt
class PeriodicArray:
"""A class to represent a periodic signal, using a single
period of the sequence.
"""
def __init__(self, base):
"""base is the base sequence representing a full period."""
self.base = base
@property
def N(self):
"""Lenght of the base array, which is also the
period of our infinite-periodic sequence"""
return len(self.base)
def __getitem__(self, n):
"""We can get the value at any index, from -infinity
to +infinity using the fact that the sequence is N-
periodic, so we use the modulo operator.
Examples
--------
>>> x = PeriodicArray([1, 2, 3])
>>> x[0]
1
>>> x[4]
2
>>> x[5]
3
"""
return self.base[n%self.N]
def plot(self, ax=None):
"""Quickly plot the sequence, with a period before and after
the base array."""
if ax is None:
fig, ax = plt.subplots()
line = ax.plot(self.base, '-o')
ax.plot(np.arange(-self.N, 0), self.base, '--o', color=line[0].get_color(), alpha=0.5)
ax.plot(np.arange(self.N, self.N*2), self.base, '--o', color=line[0].get_color(), alpha=0.5)
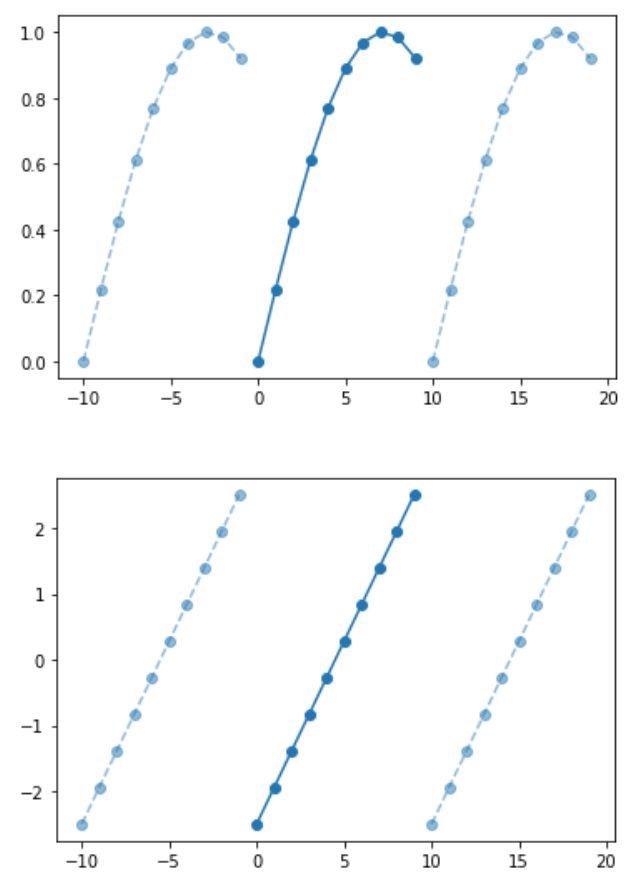
return ax让我们看两个例子:首先是采样的窦序列,然后是线性序列。两者都被认为是 N 周期性的(在这种情况下为 N=10)。
periodic_sampled_sinus = PeriodicArray(np.sin(2*np.pi*1*np.linspace(0, np.pi/10, 10)))
periodic_sampled_sinus.plot()
periodic_slope = PeriodicArray(np.linspace(-5, 5, num=10)*0.5)
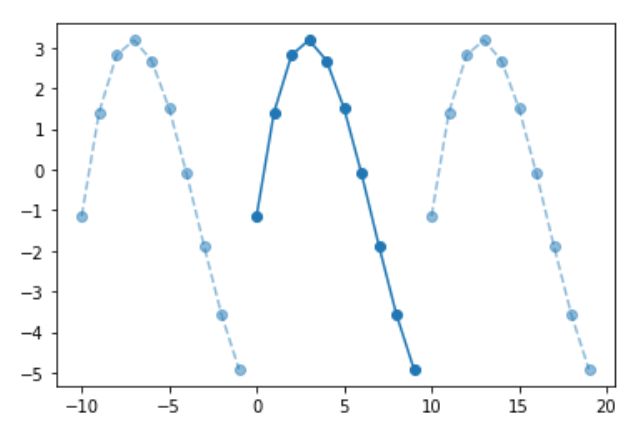
periodic_slope.plot()PeriodicArray 的 2 个示例:“基”周期以深蓝色从 0 到 N 绘制,而其他 2 个周期在前后添加,以表示我们正在处理周期序列的事实(由作者制作)。
六、循环卷积,慢速方式
现在让我们实现上面看到的循环卷积方程。使用索引和模运算符,非常简单:
上述2个周期序列之间的循环卷积(由作者制作)。
太好了,我们现在可以看到两个信号之间的循环卷积是什么样子的。将所有内容放在一个数字中:
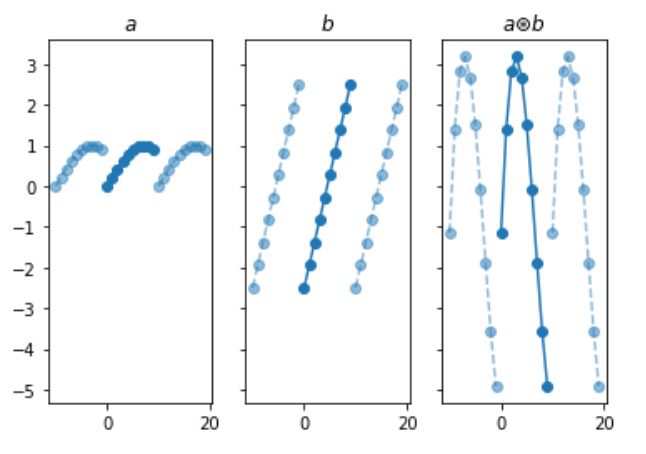
左:第一个周期数组。中间:第二周期数组。右:2个周期数组的循环卷积,这也是一个周期数组(由作者制作)。
现在这个解决方案运行得很好,但它有一个主要缺陷:它很慢。如您所见,我们必须经历 2 个嵌套循环来计算结果:一个用于结果数组中的每个位置,一个用于计算该位置的结果:我们说算法是 O(N²),随着 N 的增加,操作次数将随着 N 的平方而增加。
对于示例中的小型数组,这不是问题,但随着数组的增长,它将成为主要问题。
此外,在python中,对数值数据的循环在大多数情况下被认为是一种不好的做法。一定有更好的方法...
七、循环卷积,傅里叶方式
这就是傅里叶变换和卷积定理发挥作用的地方。由于离散傅里叶变换的实现方式,使用快速傅里叶变换(FFT)以非常快速和优化的方式实现,操作非常快(我们说FFT是O(N log N),这比O(N²)要好得多)。
使用卷积定理,我们可以利用 2 个序列的 DFT 的乘积,当使用逆 DFT 转换回时域时,我们得到输入时间序列的卷积。换句话说,我们有:
使用直接和逆傅里叶变换的x和y之间的循环卷积(由作者制作)。
其中DFT表示离散傅里叶变换,IDFT表示逆运算。
然后我们可以非常轻松地实现这个算法来计算 x 和 y 的卷积:
def circconv_fast(x, y):
"""Fast circular convolution using DFT.
Return the full array of the circulard
convolution between x and y.
"""
X = np.fft.fft(x)
Y = np.fft.fft(y)
return np.real(np.fft.ifft(np.multiply(X, Y)))
# let's compute the circular convolution for our 2 signals
circ_fast = circconv_fast(periodic_sampled_sinus.base, periodic_slope.base)
circ_fast = PeriodicArray(circ_fast)八、数值和时间比较
最后,让我们验证这两种方法是否产生相同的结果,并比较 python 使用这两种技术计算循环卷积所需的时间:
# compare both ways : "slow" way, and DFT-way
fig, ax = plt.subplots()
ax.plot(circ.base, '-o', label="slow-way")
ax.plot(circ_fast.base, '-o', label="DFT-way")
ax.legend()
ax.set_title('Comparison of 2 ways to compute convolution : \nslow-algebraic way VS using DFT and the convolution theorem')
比较两种计算两个周期序列之间循环卷积的方法:“慢速方式”是使用蓝色循环和加法的简单代数,它与橙色的“傅里叶方式”叠加。两种方法给出的结果完全相同(精确到数值精度)(由作者制作)。
这是完美的搭配!两者在数值方面是严格等效的。
现在进行时间比较:
N = 1000
long_x = np.sin(2*np.pi*1*np.linspace(0, np.pi/10, N))
long_y = np.cos(2*np.pi*1*np.linspace(0, np.pi/10, N))
print(circconv(long_x, long_y))
print(circconv_fast(long_x, long_y))
# first make sure that both method yield the same result
assert np.allclose(circconv(long_x, long_y), circconv_fast(long_x, long_y))
%timeit circconv(long_x, long_y)
%timeit circconv_fast(long_x, long_y)
# for N = 10 : 90.2 µs ± 10.2 µs for the slow way VS 14.1 µs ± 161 ns for the DFT-way
# for N = 1000 : 579 ms ± 9.14 ms for the slow way VS 69.4 µs ± 2.35 µs for the DFT-way
from physipy import units
ms = units['ms']
mus = units['mus']
print("Gain in speed for 10 samples length: ", 90*mus/(14*mus))
print("Gain in speed for 1000 samples length: ", 579*ms/(69*mus))结果是:
- 对于 N=10 个样本,DFT 快 6 倍
- 对于 N=1000 个样本,DFT 的速度快约 10000 倍
这是巨大的!现在考虑一下,当您分析包含成千上万个样本的时间序列时,它可以为您带来什么!
Fourier Transform for Time Series: Fast Convolution Explained with numpy | by Yoann Mocquin | Jul, 2023 | Towards Data Science