五、模型训练
目录
- 1. 线性模型
-
- 1.1 Lasso 回归
- 1.2 Ridge 回归
- 2. 树模型
-
- 2.1 随机森林(Random Forest,RF)
- 2.2 梯度提升树(GBDT)
- 2.3 XGBoost
- 2.4 LightGBM
- 2.5 CatBoost
- 2.6 模型深入对比
- 3. 神经网络
-
- 3.1 多层感知机
- 3.2 卷积神经网络
- 3.3 循环神经⽹络
- 4 实战案例
可选择的模型主要分为线性模型、树模型和神经网络三种。
1. 线性模型
本节将介绍两种线性缩减方法:Lasso 回归和 Ridge 回归。这两种线性回归模型的区别仅在于如何进行惩罚、如何解决过拟合问题。然后对两种模型的数学形式、优缺点和应用场景进行相应介绍。
1.1 Lasso 回归
Lasso 的全称是 Least absolute shrinkage and selection operator,是对普通的线性回归便用 L 1 L_1 L1 正则化进行优化,通过惩罚或者限制估计值的绝对值值之和,可以使某些系数为雩,从而达到特征系数化和特征选择的效果。
当我们需要一些自动的特征、变量选择,或者处理高度相关的预测因素时,这是很方便的,因为标准回归的回归系数通常太大。Lasso回归的数学形式如式: m i n ( ∣ ∣ Y − θ X ∣ ∣ 2 2 + λ ∣ ∣ θ ∣ ∣ 1 ) min(|| Y - \theta X||_2^2 + \lambda ||\theta||_1) min(∣∣Y−θX∣∣22+λ∣∣θ∣∣1)其中, λ \lambda λ 是正则项(惩罚项)的系数,通过改变 λ \lambda λ 的值,基本上可以控制惩罚项,即 θ \theta θ 的 L 1 L_1 L1 范数。当入的值越高,惩罚项的影响程度越大,反之越小。
代码实现
可以直接调用 sklearn 库来实现 Lasso 回归,这里选择的 L 1 L_1 L1 正则参数是 0.1。
from sklearn.linear_model import Lasso
lasso_model = Lasso(alpha = 0.1, normalize = True)
1.2 Ridge 回归
Ridge 回归是对普通的线性回归使用 L 2 L_2 L2 正则进行优化,对特征的权重系数设置了惩罚项。其数学形式如式: m i n ( ∣ ∣ Y − θ X ∣ ∣ 2 2 + λ ∣ ∣ θ ∣ ∣ 2 2 ) min(|| Y - \theta X||_2^2 + \lambda ||\theta||_2^2) min(∣∣Y−θX∣∣22+λ∣∣θ∣∣22)与 Lasso 回归的损失函数基本一致,只是将惩罚项修改成了 θ \theta θ 的 L 2 L_2 L2 范数。
代码实现
可以直接调用 sklearn 库来实现 Ridge 回归∶
from sklearn.linear_model import Ridge
Ridge_model = Ridge(alpha=0.05, normalize=True)
考虑一个例子:假设现在有一个非常大的数据集,其中包含 10000 个特征。这些特征中仅有部分特征是相关的。然后思考一下,应该用哪个回归模型进行训练,是Lasso回归还是Ridge回归?
- 如果我们用 Lasso 回归进行训练,那么遇到的困难主要是当存在相关特征时,Lasso 回归只保留其中一个特征,而将其他相关特征设置为零。这可能会导致一些信息丢失,从而降低模型预测的准确性。
- 如果选择 Ridge 回归,虽然能降低模型的复杂性,但并不会减少特征的数量,因为Ridge回归从不会使系数为零,而只会使系数最小化(即仍然会选择所有特征),可是这并不利于特征缩减。在面对 10000 个特征时,模型仍然会很复杂,因此可能会导致模型性能不佳。
- 综合考虑,这个问题的解决办法是什么呢?可以选择弹性网络回归 (Elastic Net Regression),见参考文章。
2. 树模型
本节将介绍竞赛中常见的树模型,这些模型简单易用,能够带来高收益。可将树模型分为随机森林 (Random Forest,RF) 和梯度提升树 (GBDT),这两者最大的差异是前者并行、后者串行。在梯度提升树部分我们将介绍如今竞赛中大火的三种树模型:XGBoost、LightGBM 和 CatBoost。
2.1 随机森林(Random Forest,RF)
简言之,随机森林算法就是通过集成学习的思想将多个决策树集成在一起。这里的决策树可以是一个分类器,各个决策树之间没有任何关联,随机森林算法对多个决策树的结果进行投票得到最终结果,这也是最简单的 Bagging 思想。随机森林是一个基于非线性树的模型,通常可以提供准确的结果。
-
随机森林的构造过程
随机森林的构造过程如图所示。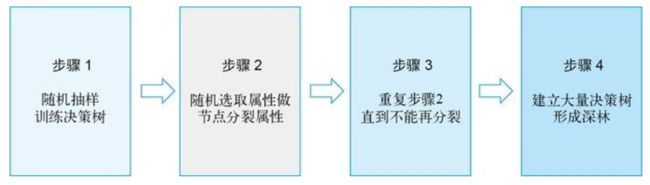
- 假设训练集中的样本数为 N N N。有放回的随机抽取 N N N 个样本,即样本可以重复,然后用得到的这 N N N 个样本来训练一棵决策树。
- 如果有 M M M 个输入变量(特征),则指定一个远小于 M M M 的数字 m m m (列采样),以便在每次分裂时,都从 M M M 个输入变量中随机选出 m m m 个。然后从选出的这 m m m 个变量中选择最佳分裂变量(分裂依据信息增益、信息增益比、基尼指数等)。
- 重复步骤 2,对每个节点都进行分裂,并且不修剪,使节点最大限度地生长(停止分裂的条件为节点的所有样本均属于同一类)。
- 通过步骤 1 到 3 构造大量决策树,然后汇总这些决策树以预测新数据(对分类问题进行投票选择,对回归问题进行均值计算)。
-
随机森林的优缺点
- 随机森林优点非常明显:不仅可以解决分类和回归问题,还可以同时处理类别特征和数值特征;不容易过拟合,通过平均决策树的方式,降低过拟合的风险;非常稳定,即使数据集中出现了一个新的数据点,整个算法也不会受到过多影响,新的数据点只会影响到一棵决策树,很难对所有决策树都产生影响。
- 很多缺点都是相对而言的,随机森林算法虽然比决策树算法更复杂,计算成本更高,但是其拥有天然的并行特性,在分布式环境下可以很快地训练。梯度提升树需要不断地训练残差,所以结果准确度更高,但是随机森林更不容易过拟合,更加稳定,这也是因为其 Bagging 的特性。
-
代码实现
from sklearn.ensemble import RandomForestClassifier rf = RandomForestClassifier(max_features='auto', oob_score=True, random_state=1, n_jobs=-1)
2.2 梯度提升树(GBDT)
梯度提升树(GBDT)是基于 Boosting 改进而得的,在 Boosting 算法中,一系列基学习器都需要串行生成,每次学习一棵树,学习目标是上棵树的残差。和 AdaBoost 一样,梯度提升树也是基于梯度下降函数。梯度提升树算法已被证明是 Boosting 算法集合中最成熟的算法之一,它的特点是估计方差增加,对数据中的噪声更敏感(这两个问题都可以通过使用子采样来减弱),以及由于非并行操作而导致计算成本显著,因此要比随机森林慢很多。
梯度提升树作为 XGBoost、LightGBM 和 CatBoost 的基础,这里将对其原理进行简单介绍。我们知道梯度提升树是关于 Boosting 的加法模型,由 K K K 个模型组合而成,其形式如式:
y ^ i = ∑ k = 1 K f k ( x i ) f k ∈ F \hat{y}_i = \sum_{k=1}^K f_k(x_i) \ \ \ \ f_k \in F y^i=k=1∑Kfk(xi) fk∈F
一般而言,损失函数描述的是预测值 y y y 与真实值 y ^ \hat{y} y^ 之间的关系,梯度提升树是基于残差( y i − F x i , F x i y_i - F_{x_i},F_{x_i} yi−Fxi,Fxi为前一个模型)来不断拟合训练集的,这里使用平方损失函数。那么对于 n n n 个样本来说,则损失函数可以写成式
L = ∑ i = 1 n l ( y i , y ^ i ) L = \sum_{i=1}^n l (y_i, \hat{y}_i) L=i=1∑nl(yi,y^i)
更进一步,目标(损失)函数可以写成式:
O b j = ∑ i = 1 n l ( y i , y ^ i ) + ∑ k = 1 K Ω ( f k ) Obj = \sum_{i=1}^n l (y_i, \hat{y}_i) + \sum_{k=1}^K \Omega(f_k) Obj=i=1∑nl(yi,y^i)+k=1∑KΩ(fk)
其中 Ω \Omega Ω 代表基模型的复杂度,若基模型是树模型,则树的深度、叶子节点数等指标均可以反映树的复杂度。
对于 Boosting 来说,它采用的是前向优化算法,即从前往后逐渐建立基模型来逼近目标函数,具体过程如式:
y ^ i 0 = 0 y ^ i 1 = f 1 ( x i ) = y ^ i 0 + f 1 ( x i ) y ^ i 2 = f 1 ( x i ) + f 2 ( x i ) = y ^ i 1 + f 2 ( x i ) ⋮ y ^ i t = ∑ k = 1 t f k ( x i ) = y ^ i t − 1 + f t ( x i ) \begin{aligned} \hat{y}_i^0 &= 0 \\ \hat{y}_i^1 &= f_1(x_i) = \hat{y}_i^0 + f_1(x_i) \\ \hat{y}_i^2 &= f_1(x_i) + f_2(x_i) = \hat{y}_i^1 + f_2(x_i) \\ \vdots \\ \hat{y}_i^t &= \sum_{k=1}^t f_k(x_i) = \hat{y}_i^{t-1} + f_t(x_i) \end{aligned} y^i0y^i1y^i2⋮y^it=0=f1(xi)=y^i0+f1(xi)=f1(xi)+f2(xi)=y^i1+f2(xi)=k=1∑tfk(xi)=y^it−1+ft(xi)
那么在逼近过程的每一步中,如何学习一个新的模型呢?答案的关键还是在梯度提升树的目标函数上,即新模型的加入总是以优化目标函数为目的。重写目标函数如式:
O b j t = ∑ i = 1 n l ( y i , y ^ i t ) + ∑ i = 1 t Ω ( f i ) O b j t = ∑ i = 1 n l ( y i , y ^ i t − 1 + f t ( x i ) ) + Ω ( f t ) + constant \begin{aligned} Obj^t &= \sum_{i=1}^n l (y_i, \hat{y}_i^t) + \sum_{i=1}^t \Omega(f_i) \\ Obj^t &= \sum_{i=1}^n l (y_i, \hat{y}_i^{t-1} + f_t(x_i)) + \Omega(f_t) + \text{constant} \\ \end{aligned} ObjtObjt=i=1∑nl(yi,y^it)+i=1∑tΩ(fi)=i=1∑nl(yi,y^it−1+ft(xi))+Ω(ft)+constant
将 f t ( x i ) f_t(x_i) ft(xi) 泰勒展开到二阶后有下式:
O b j t = ∑ i = 1 n [ l ( y i , y ^ i t − 1 ) + g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) + constant Obj^t = \sum_{i=1}^n \left [ l (y_i, \hat{y}_i^{t-1}) + g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i) \right ] + \Omega(f_t) + \text{constant} Objt=i=1∑n[l(yi,y^it−1)+gift(xi)+21hift2(xi)]+Ω(ft)+constant
移除常数项:
O b j t ≈ ∑ i = 1 n [ l ( y i , y ^ i t − 1 ) + g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) Obj^t \approx \sum_{i=1}^n \left [ l (y_i, \hat{y}_i^{t-1}) + g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i) \right ] + \Omega(f_t) Objt≈i=1∑n[l(yi,y^it−1)+gift(xi)+21hift2(xi)]+Ω(ft)
之所以要移除常数项,是因为函数中的常量在函数最小化的过程中不起作用。
这样一来,梯度提升树的最优化目标函数就变得非常统一,它只依赖于每个数据点在误差函数上的一阶导数和二阶导数,然后根据加法模型得到一个整体模型。
2.3 XGBoost
XGBoost 是基于决策树的集成机器字习算法法,它以梯度提升 (GradientBoost)为框架。在 SIGKDD 2016大会上,陈天奇 和 Carlos Guestrin 发表的论文 "XGBoost: A Scalable Tree Boosting system” 在整个机器学习领域都引起了轰动,并逐渐成为 Kaggle 和数据科学界的主导。
XGBoost 同样也引入了 Boosting 算法。XGBoost 除了在精度和计算效率上取得成功的性能外,还是一个可扩展的解决方案。由于对初始树 Boost GBM 算法进行了重要调整,因此 XGBoost 代表了新一代的 GBM 算法。
-
主要特点
- 采用稀疏感知算法,XGBoost可以利用稀疏矩阵,节省内存(不需要密集矩阵)和节省计算时间(零值以特殊方式处理)。
- 近似树学习(加权分位数略图),这类学习方式能得到近似的结果,但比完整的分支切割探索要省很多时间。
- 在一台机器上进行并行计算(在搜索最佳分割阶段使用多线程),在多台机器上进行类似的分布式计算。
- 利用名为核外计算的优化方法,解决在磁盘读取数据时间过长的问题。将数据集分成多个块存放在磁盘中,使用一个独立的线程专门从磁盘读取数据并加载到内存中,这样一来,从磁盘读取数据和在内存中完成数据计算就能并行运行。
- XGBoost 还可以有效地处理缺失值,训练时对缺失值自动学习切分方向。基本思路是在每次的切分中,让缺失值分别被切分到大策树的左节点和右节点,然后通过计算增益得分选择增益大的切分方向进行分裂,最后针对每个特征的缺失值,都会学习到一个最优的默认切分方向。
-
代码实现
import xgboost as xgb params = {'eta': 0.01, 'max_depth': 11,'objective': 'reg:linear', 'eval_metric': 'rmse' } dtrain = xgb.DMatrix(data=X_train, label=y_train) dtest = xgb.DMatrix(data=X_valid, label=y_valid) watchlist = [(train_data, 'train'), (valid_data, 'valid_data')] model = xgb.train(param, train_data, num_boost_round=20000, evals=watchlist, early_stopping_rounds=200, verbose_eval=500) y_pred = model.predict(xgb.DMatrix(X_test), ntree_limit=model.best_ntree_limit)
2.4 LightGBM
LightGBM 是微软的一个团队在 Github 上开发的一个开源项目,高性能的 LightGBM 算法具有分布式和可以快速处理大量数据的特点。
LightGBM 虽然基于决策树和 XGBoost 而生,但它还遵循其他不同的策略。XGBoost 使用决策树对一个变量进行拆分,并在该变量上探索不同的切割点(按级别划分的树生长策略),而 LightGBM 则专注于按叶子节点进行拆分,以便获得更好的拟合(这是按叶划分的树生长束略)。这使得 LightGBM 能够快速获得很好的数据拟合,并生成能够替代 XGBoost 的解决方案。从算法上讲,XGBoost 将决策树所进行的分割结构作为一个图来计算,使用广度优先搜索 (BFS),而 LightGBM 使用的是深度优先搜索 (DFS)。
-
主要特点
- 比 XGBoost 准确性更高,训练时间更短。
- 支持并行树增强,即使在大型数据集上也能提供比XGBoost 更好的训练速度。
- 通过使用直方图算法将连续特征提取为离散特征,实现了惊人的快速训练速度和较低的内存使用率。
- 通过使用按叶分割而不是按级别分割来获得更高精度,加快目标函数收敛过程,并在非常复杂的树中捕获训练数据的底层模式。使用 num_ leaves 和 max_depth 超参数控制过拟合。
-
代码实现
import lightgbm as lgb params = {'num_leaves': 54, 'objective': 'regression', 'max_depth': 18, 'learning_rate': 0.01, 'boosting': 'gbdt', 'metric': 'rmse', 'lambda_l1': 0.1} model = lgb.LGBMRegressor(**params, n_estimators = 20000, nthread =4, n_jobs = -1) model.fit(X_train, y_train, eval_set=[(X_train, y_train), (X_valid, y_valid)], eval_metric='rmse', verbose=1000, early_stopping_rounds=200) y_pred = model.predict(X_test, num_iteration=model.best_iteration_)
2.5 CatBoost
CatBoost 是由俄罗斯搜索引擎 Yandex 在2017年7月开源的一个 GBM 算法,它最强大的一点是能够采用将独热编码和平均编码混合的策略来处理类别特征。
CatBoost 用来对类别特征进行编码的方法并不是新方法,是均值编码,该方法已经成为一种特征工程方法,被广泛应用于各种数据科学竞赛中,如Kaggle。
均值编码,也称为似然编码、影响编码或目标编码,可将标签转换为基于它们的数字,并与目标变量相关联。如果是回归问题,则基于级别典型的平均目标值转换标签;如果是分类问题,则仅给定标签的目标分类概率(目标概率取决于每个类别值)。均值编码可能看起来只是一个简单而聪明的特征工程技巧,但实际上它也有副作用,主要是过拟合,因为会把目标信息带入预测中。
-
主要特点
-
支持类别特征,因此我们不需要预处理类别特征(例如通过 labeencoding 或独热编码)。事实上,CatBoost文档中讲到不要在预处理期间使用独热编码,因为 “这会影响训练速度和结果质量”。
-
提出了一种全新的梯度提升机制 (Ordered Boosting) ,不仅可以减少过拟合的风险,也大大提高了准确性。
-
支持开箱即用的 GPU训练(只需设 task_type=“GPU”)
-
CatBoost 目前支持输入文本特征,因此不需要像以前那样先进行烦琐的操作获得标准化输入,再喂给模型。文本特征跟类别特征的标记方式一样,只需在训练时把文本变量名的列表赋给 text_features 即可。那么 CatBoost 内部是怎么处理文本特征的呢?操作其实非常常规,CatBoost 内部将输入的文本特征转化为了数值特征,具体过程是分词、创建字典、将文本特征转化为多值的数值特征,接下来的处理方法可选择项就比较多了,比如完全展开成布尔型 0/1 特征,或者进行词频统计等。
-
训练中使用了组合类别特征,利用了特征之间的联系,极大丰富了特征维度。
-
-
深入理解特征组合
CatBoost 另一个强大的功能是在树分裂选择节点的时候能够将所有类别特征之间的组合考虑进来,即能够对两个类别特征进行组合。具体做法是,第一次分裂时不考虑类别特征的组合,之后分裂时会考虑类别特征之间的组合,使用贪心算法生成最佳组合,然后将组合后的类别特征转化为数值型特征。CatBoost 会把分裂得到的两组值作为类别型特征参与后面的特征组合,以实现更细粒度的组合。 -
代码实现
from catboost import CatBoostRegressor params = {'learning_rate': 0.02,'depth': 13,'bootstrap_type': 'Bernoulli', 'od_type': 'Iter', 'od_wait': 50, 'random_seed': 11} model = CatBoostRegressor(iterations=20000, eval_metric='RMSE', **params) model.fit(X_train, y_train, eval_set=(X_valid, y_valid), cat_features=[], use_best_model=True, verbose=False) y_pred = model.predict(X_test)
2.6 模型深入对比
-
决策树生长策略
下面列出了三种决策树的生长方式:
- XGBoost 使用的是 Level-wise 按层生长,可以同时分裂同一层的叶子,从而进行多线程优化,不容易过拟合,但很多叶子节点的分裂增益较低,会影响性能。
- LightGBM使用的是 Leaf-wise 分裂方式,每次都从当前叶子中选择增益最大的结点进行分裂,循环迭代,但会生长出非常深的决策树从而导致过拟合,这时可以调整参数 max_depth 来防止过拟合。
- CatBoost 使用的是oblivious-tree(对称树),这种方式使得节点是镜像生长的。相对于传统的生长策略,oblivious-tree 能够简单拟合方案,快速生成模型,这种树结构起到了正则化的作用,因此并不容易过拟合。
-
梯度偏差(Gradient Bias)
XGBoost 和 LightGBM中的提升树算法都是有偏梯度估计,在梯度估计中使用的数据与目前建立的模型所使用的数据是相同的,这样会导致数据发生泄漏,从而产生过拟合。CatBoost 改进了提升树算法,将原来的有偏梯度估计转换为了无偏梯度估计。具体做法是利用所有训练集(除第 i i i 条)建立模型 M i M_i Mi,然后使用第 1 1 1 条到第 i − 1 i-1 i−1 条数据来建一个修正树 M M M,累加到原来的模型 M i M_i Mi 上。
-
类别特征处理
- XGBoost 并不能处理类别特征,因此需要我们根据数据实际情况进行独热编码、count 编码和目标编码。
- LightGBM 直接支持类别特征,不需要独热展开。这里使用 manyvs-many 的切分方式来处理类别特征,并且可以把搜索最佳分割点的时间复杂度控制在线性级别,和原来 one-vs-other 方式的时间复杂度几乎一致。该算法先按照每个类别对应的标签均值(即 avg(y)=Sum(y)/Count(y))进行排序,然后根据排序结果依次枚举最优分割点。和数值型特征的切分方式不同,它是将某一类别当作类,然后将其余所有类别作为一类。
- CatBoost 在处理类别特征方面做了更细致的操作。或许在使用 LightGBM 时,还需要对类别特征进行更多的编码方式,但对于 CatBoost,则可以选择不进行多余的编码方式。具体实现流程是首先对输入的样本集随机排序,然后针对类别特征中的某个取值,在将每个样本的该特征转换为数值型时,都基于排在该样本之前的类别标签取均值。对所有的类别特征值结果都进行如下式所示的运算,使之转化为数值结果。其中 [ ] \left [ \ \right ] [ ] 是指示函数,当方括号内两个元素相等时取 1,反之取 0。 a (a >0) 是先验值 p p p 的权重,添加先验值是一种常见的做法,这有助于减少从低频类别中获得的噪声、降低过拟合。对于回归问题,将标签的平均值作为先验值;对于分类问题,将正类出现的概率作为先验值。
∑ j = 1 p − 1 [ x σ j , k = x σ p , k ] × Y σ j + a × P ∑ j = 1 p − 1 [ x σ j , k = x σ p , k ] + a \frac{\sum_{j=1}^{p-1} \left [ x_{\sigma_j, k} = x_{\sigma_p, k} \right ] \times Y_{\sigma_j} + a \times P }{\sum_{j=1}^{p-1} \left [ x_{\sigma_j, k} = x_{\sigma_p, k} \right ] + a} ∑j=1p−1[xσj,k=xσp,k]+a∑j=1p−1[xσj,k=xσp,k]×Yσj+a×P
-
参数对比
如下图所示,从三个方面对树模型的参数进行对比,分别是用于控制过拟合、用于控制训练速度和调整类别特征的三类参数。这里只是枚举一些重要的参数,还有大量有用的参数就不一一进行介绍了。
3. 神经网络
如果想在竞赛的道路上走得更远,那么神经网络也是必须要掌握的模型。一般而言,随着我们拥有的数据量不断增加,神经网络战胜传统传统机器学习模型的可能性也会加大。
首先举一个房屋价格的例子来展示神经网络的功能细节,具体要根据房屋的某些功能估算房屋的价格。如果提供的是房屋大小、位置和卧室数量等详细信息,要求估算房屋价格,那么此时神经网络将是最适合的方法。
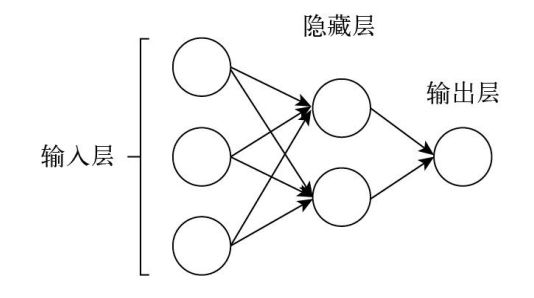
如图下图所示描述了神经网络的简单结构,它具有三种不同类型的层:输入层、隐藏成和输出层。每个隐藏层可以包含任意数量的神经元(节点),输入层中节点的数量等于预测问题中使用的特征数量(上面示例中有3个特征,即房屋大小、位置和卧室数量),输出层中节点的数量等于要预测的值的数量(上面示例中要预测的值有1个,即房屋价格)。接下来,我们尝试更深入一点,了解每个节点中正在发生的事情。
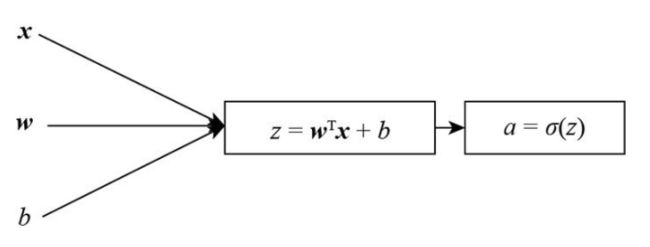
如下图所示,在输入层的各个节点中,将输入要素 x x x、权重 w w w 和偏置 b b b 作为输入,计算并输出 z z z。将这些值构造成矩阵,可使计算变得更加容易和高效。什么是权重(weight)和偏置(bais)?这两个值首先是从高斯分布中随机初始化的值,用于计算输入节点的输出,我们通过调整这些值来让神经网络拟合输入的数据。

如下图所示,在计算出值 z z z 之后,我们对 z z z 使用激活函数 σ \sigma σ。激活函数用于向模型引入一些非线性。如果我们不应用任何激活函数,则输出结果只能是线性函数,并且可能无法成功地将复杂输入映射到输出。
隐藏层中节点的输入是上一层节点的输出。最后的输出层会预测一个值,对该值与已知值(真实值)进行比较,就可计算出损失。从直觉上讲,损失表示预测值与真实值之间的误差。
整个过程先是计算出每个变量以及每层的权重并计算误差(前向传播),然后通过反向传播遍历每个层来测量每个连接的误差贡献,最后稍微调整连接器的权重和偏置来减少误差,以确保对输出结果进行正确的预测。
到目前为止,我们对神经网络已经有了基本的认识。接下来将介绍多层感知机、卷积神经网络和循环神经网络。
3.1 多层感知机
多层感知机(MLP)也可以称作深度神经网络(Deep Neural Networks,DNN),就是含有多个隐藏层的神经网络。单个感知机尚且具有一定的拟合能力,多层感知机必将拥有更强大的拟合能力,可以用于解决更为复杂的问题。
如下图所示,给出了多层感知机最基本的结构,主要分为输入层、隐藏层和输出层。多层感知机的不同层之间均是全连接的(全连接∶指的是第 i i i 层中任意神经元一定与第 i + 1 i+1 i+1 层中任意神经元相连接)。接下来还需要详细学习三个主要参数∶权重、偏置和激活函数。

-
权重与偏置
权重用于表示神经元之间的连接强度,权重的大小表示可能性大小。设置偏置是为了正确分类样本,这是模型中一个重要的参数,即保证通过输入算出的输出值不能被随便激活。 -
激活函数
激活函数可以起到非线性映射的作用,可以将神经元的输出幅度限制在一定范围内,一般在 (-1,1)或(0,1)之间。常用的激活函数有 sigmoid、tanh、ReLU 等,其中 sigmoid 函数可将 (-∞,+∞) 之间的数映射到(0,1)范围内,其余的函数这里不做过多介绍。 -
代码实现
def create_mlp(shape): X_input = Input((shape, )) X = Dense(256, activation='relu')(X_input) X = Dense(128, activation='relu')(X) X = Dense(64, activation='relu')(X) X = Dense(1, activation='sigmoid')(X) model = Model(inputs=X_input, outputs=X) model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy']) return model mlp_model = create_mlp(x_train.shape[0]) mlp_model.fit(x=x_train, y=y_train, epochs=30, batch_size=512)
3.2 卷积神经网络
卷积神经网络(CNN)类似于多层感知机,两者的区别在于网络结构不同。卷积神经网络的提出是受生物处理过程的后发,其结构与动物视觉皮层具有相似性。卷积神经网络广泛应用于计算机视觉领域,比如人脸识别、自动驾驶、图像分割等,并在各种竞赛案例上取得了优异的成绩。卷积神经网络有两大特点:
- 能够有效地将大数据量的图片降维成小数据量,简化复杂问题。部分场景下,降维并不会影响结果。比如一张图片中有只猫,将该图片的像素从 1000 缩小成 200 后,即使肉眼看,也不会将其中的猫认成狗,机器也是如此。
- 能够有效保留图像特征,并且符合图像处理的原则。对图像进行翻转、旋转或者变换位置的操作时,卷积神经网络能够有效识别出哪些是类似的图像。
如下图所示,给出了卷积神经网络最基本的结构,主要分为三层:卷积层、池化层((采样层)和全连接层。三层各司其职,卷积层负责提取特征,池化层负责特征选择,全连接层负责分类。全连接层就是我们前面讲到的神经网络,所以接下来只对卷积层和池化层进行详细介绍。

-
卷积层(convolutional layer)
卷积层用于提取图像中的局部特征,可以有效降低数据维度。如下图所示假设我们的输入的 RGB 图像大小为32×32,因为含 3 种颜色的通道,所以输入的实际大小是 32×32×3。然后选择 5x5 的卷积核进行卷积计算,加之包含三个通道,所以每次提取 5x5×3 大小的方块,将提取步长(stride)设置为 1,并且不向外侧进行填充(padding=0),最后可以得到 28×28×1 的特征图。
-
池化层(pooling layer)
池化层用于特征选择,相比卷积层可以更有效地降低数据维度,不但能大大减少运算量,还能有效避免过拟合。例如,当数据经过卷积层得到 28×28×1 的特征图后,我们设置步长为 2,卷积核大小是 2×2,然后经过最大池化层/平均池化层,得到14×14×1 的新特征图,如下图所示。有了上面对基本结构的介绍,我们就可以使用 keras 来构建自己的卷积神经网络了。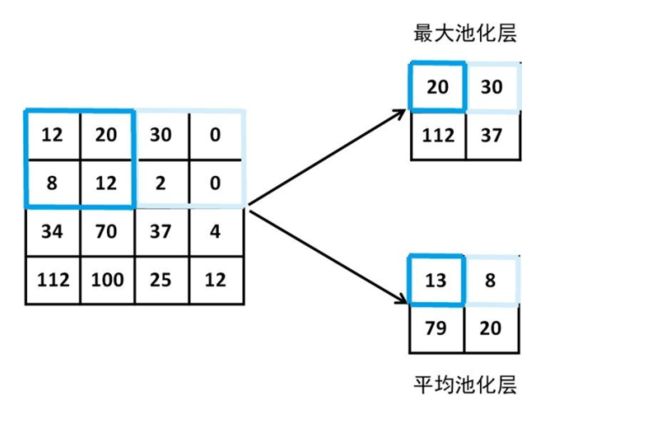
-
代码实现
def create_cnn(): X_input = Input((28,28,1)) X = Conv2D(24,kernel_size=5,padding='same',activation='relu')(X_input) X = MaxPooling2D()(X) X = Conv2D(48,kernel_size=5,padding='same',activation='relu')(X_input) X = MaxPooling2D()(X) X = Flatten()(X) X = Dense(128, activation='relu')(X) X = Dense(64, activation='relu')(X) X = Dense(1, activation='sigmoid')(X) model = Model(inputs=X_input, outputs=X) model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy']) return model cnn_model = create_cnn() cnn_model.fit(x=x_train, y=y_train, epochs=30, batch_size=64)
3.3 循环神经⽹络
循环神经网络(RNN)是神经网络的一种扩展,更擅长对序列数据进行建模处理。对于传统的前馈神经网络,输入一般是一个定长的向量,无法处理变长的序列信息,即使通过一些方法把序列处理成定长的向量,模型也很难捕捉序列中的长距离依赖关系。循环神经网络通过将神经元串行起来的方式处理序列化的数据。由于每个神经元都能用其内部变量保存之前输入的序列信息,因此整个序列被浓缩成抽象的表示,并可以据此进行分类或生成新的序列。
对序列数据进行处理以及用序列数据完成分类决策或回归估计时,循环神经网络是非常有效的,它通常用于解决与序列数据相关的任务,主要包括自然语言处理、语音识别、机器翻译、时间序列预测等。当然,循环神经网络也可以用于非序列数据。
如下图所示为循环神经网络的基本结构,它由一个神经元接收输入,产生一个输出,并将输出返回给自己,如下图中(1) 所示。在每个时间步 t t t (也称为一个帧),循环神经元接收输入 t t t 以及它自己的前一时间步长 h t − 1 h_{t-1} ht−1。我们可以按照时间轴将(1)推移展开成网络,如图下图中 (2) 所示。

用公式表示如下:
y t = g ( V ⋅ h t ) h t = f ( U ⋅ X t + W ⋅ h t − 1 ) \begin{aligned} y_t &= g(V \cdot h_t) \\ h_t &= f(U \cdot X_t + W \cdot h_{t-1}) \end{aligned} ytht=g(V⋅ht)=f(U⋅Xt+W⋅ht−1)
其中, V V V 是隐藏层到输出层的权重矩阵, U U U 是输入层到隐藏层的权重矩阵, W W W 也是权重矩阵,表示隐藏层上一次的值作为这一次输入的权重。另外, X X X 为输入层, h h h 为隐藏层, y y y 为输出层。
- 代码实现
不同于其他模型,循环神经网络的输入数据包含序列信息,例如,我们要对一个电影评论分类,需要进行预处理,如果文本长度不一致,需要利用 pad_sequences 进行截断,保证每个样本序列的长度一致。下面给出简单的实现代码,其中 X_train 是已经预处理好的训练集。def create_rnn(): emb = Embedding(10000, 32) # 10000 为总单词个数,32 为输出维度 X = SimpleRNN(32)(emb) X = Dense(256, activation='relu')(X) X = Dense(128, activation='relu')(X) X = Dense(1, activation='sigmoid')(X) model = Model(inputs=X_input, outputs=X) model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy']) return model rnn_model = create_rnn() rnn_model.fit(x=x_train, y=y_train, epochs=30, batch_size=64)
4 实战案例
这部分内容没有太多价值,而且现在神经网络多使用 Pytorch 搭建,所以这里没有记录书上的内容。