(MIT6.045)自动机、可计算性和复杂性-正则表达式
语言(language)的计算性质:交、并、补、反转、拼接、星号(*)

星号是一元运算符,表示一个语言和自己的有穷次笛卡尔积。
回顾:正则语言(Regular Language)指可以用DFA描述的语言。
正则表达式
一个定理:
语言L可以被表示成某种正则表达式,iff语言L是正则的(可以用DFA描述)。
Generalized-NFA
将一个DFA写成正则表达式。从DFA读取单个字符(太麻烦)变为读取一个子串。
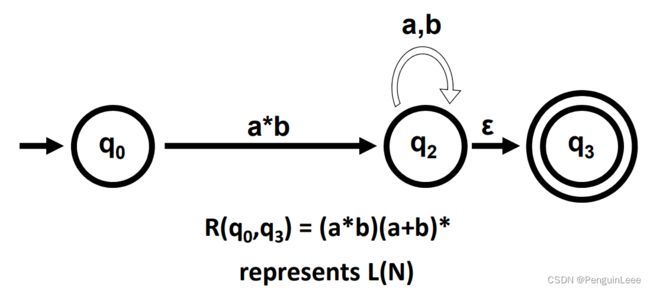
再举一个例子。通过下面的步骤,我们可以将一个NFA转化成一个只有两个状态(起始和终止状态)的generalized-NFA。

许多语言是不正则的。
比如:

对于上述例子中的C,我们需要时刻记住DFA和NFA的特性:有限状态(有限的记忆)。对于C,它的潜在状态可能是无穷多的,所以不能被DFA表示。
对于上述例子中的D,其结果为:

DFA最小化定理
(什么意义下的最小?)
对于每个正则语言A,都有一个唯一的(在状态re-labeling的情况下)最小的DFA M ∗ M^* M∗,使得 A = L ( M ∗ ) A=L(M^*) A=L(M∗)。
一般地,最小NFA不唯一。
首先,介绍概念:
字符串 w w w区分了状态 p p p和 q q q,如果在状态 p p p和 q q q下,字符串被接受和被拒绝。
如果两个状态没法区分,那么他们就是冗余的。
于是我们可以构造等价类,每一个等价类里面的元素都是互相不可区分的。
根据上述的可区分概念,我们给出最小DFA的定义:
已知DFA M,其最小DFA M*是:
- L(M) = L(M*)
- 所有状态从起始状态开始都可达
- M*不可再约减(约减,指存在不可区分的状态)。
定理:满足上述123的状态机M*是唯一的、M的最小DFA。
由于DFA/NFA和正则表达式的等价性,我们自然会想,怎么证明两个正则表达式是等价的?
存在这样的算法,使得我们可以证明两个正则表达式等价。
Myhill-Nerode定理
对于语言L,要么有一个DFA可以描述,要么总是可以找到能骗过DFA的字符串。
和DFA的状态定义类似,我们也可以定义“状态”之间的等价关系。
设 L ⊂ Σ ∗ L \subset \Sigma^* L⊂Σ∗, x , y ∈ Σ ∗ x, y \in \Sigma^* x,y∈Σ∗。我们定义 x ≡ L y x \equiv_L y x≡Ly,当且仅当 ∀ z ∈ Σ ∗ , x z ∈ L ⟺ y z ∈ L \forall z \in \Sigma^*, xz \in L \iff yz \in L ∀z∈Σ∗,xz∈L⟺yz∈L。(显然这是个等价关系)。
注意,我们可以将这个定义和前述DFA的定义进行类比, x , y x, y x,y就像是决定了不同的状态,然后从不同的状态开始迭代。
基于这里的等价关系 ≡ L \equiv_L ≡L定义,我们可以将 Σ ∗ \Sigma^* Σ∗分成若干个等价类。
于是,Myhill-Nerode定理表明:
如果等价类数量有限,则可以构建DFA。
否则不可构建DFA。
流算法(Streaming Algorithms)
Streaming Algorithms有三个组成部分:
- 初始化(变量和赋值)
- 当下一个符号是 σ \sigma σ的时候咋办(使用 σ \sigma σ和变量的伪代码)
- 当流跑完了(伪代码的输出,比如接受/拒绝)
Streaming Algorithms和DFA有几点大的不同。
4. 这玩意可能输出不止一个比特。
5. 这玩意的存储空间(也可以说是状态)可以随着读取字符串边长逐渐增长——这意味着它可以识别非正则语言。
6. 可以随机化、多通路
一个例子:

注意:和冯诺伊曼计算机不同,这里的存储空间使用不包括算法本身的存储。
DFA和流算法
定理: L ′ L' L′可以被DFA M M M(有 2 p 2^p 2p个状态)识别,那么 L ′ L' L′就可以被流算法A用p比特空间计算。
当alphabet的元素不止有0和1怎么办?






