基于LSTM深度学习网络的时间序列预测matlab仿真

目录

1.算法理论概述

1.1、LSTM深度学习网络

1.3、时间序列预测模型

2.部分核心程序

3.算法运行软件版本

4.算法运行效果图预览

5.算法完整程序工程

---

1.算法理论概述

        时间序列预测是一类重要的预测问题，在很多领域都有着广泛的应用，如金融、交通、气象等。然而，由于时间序列数据本身具有时序性和相关性，因此预测难度较大。传统的时间序列预测方法大多采用统计学方法，如ARIMA模型、指数平滑法等，但这些方法在处理非线性、非平稳、非高斯的时间序列数据时效果较差。随着深度学习技术的发展，基于深度学习的时间序列预测方法逐渐成为研究热点。本文提出了一种基于LSTM深度学习网络的时间序列预测方法，该方法能够有效地处理非线性、非平稳、非高斯的时间序列数据。

1.1、LSTM深度学习网络

       LSTM（Long Short-Term Memory）是一种特殊的RNN（Recurrent Neural Network）模型，它能够有效地处理长序列数据，并且能够捕捉时间序列中的长期依赖关系。LSTM模型包含三个门控单元：输入门、遗忘门和输出门，这些门控单元能够控制信息的流动和保留，从而实现长期依赖关系的学习。

LSTM的具体计算过程如下：

1.输入门

       输入门控制着输入信息的流入，它包含一个sigmoid函数和一个tanh函数，分别表示输入信号的重要性和输入信号的值。输入门的计算公式如下：

$$
i_t=\sigma(W_i\cdot[x_t,h_{t-1}]+b_i)
$$

$$
\tilde{C}t=\tanh(W_c\cdot[x_t,h{t-1}]+b_c)
$$

其中，$W_i$、$W_c$、$b_i$、$b_c$是LSTM模型的参数，$x_t$是当前时刻的输入，$h_{t-1}$是上一时刻的输出，$\sigma$表示sigmoid函数，$\cdot$表示矩阵乘法。

2.遗忘门

       遗忘门控制着上一时刻的输出$h_{t-1}$中哪些信息需要保留，它也包含一个sigmoid函数和一个tanh函数，分别表示上一时刻输出的重要性和输出值。遗忘门的计算公式如下：

$$
f_t=\sigma(W_f\cdot[x_t,h_{t-1}]+b_f)
$$

其中，$W_f$、$b_f$是LSTM模型的参数。

3.细胞状态

      细胞状态是LSTM模型的核心，它负责长期依赖关系的学习和保留。细胞状态的计算公式如下：

$$
C_t=f_tC_{t-1}+i_t\tilde{C}_t
$$

4.输出门

       输出门控制着细胞状态中哪些信息需要输出，它也包含一个sigmoid函数和一个tanh函数，分别表示输出的重要性和输出值。输出门的计算公式如下：

$$
o_t=\sigma(W_o\cdot[x_t,h_{t-1}]+b_o)
$$

$$
h_t=o_t*\tanh(C_t)
$$

其中，$W_o$、$b_o$是LSTM模型的参数。

1.3、时间序列预测模型

基于LSTM深度学习网络的时间序列预测模型主要包括以下步骤：

1.数据预处理

       将原始时间序列数据转化为可以被LSTM模型处理的数据格式。通常采用滑动窗口的方法将时间序列数据转化为多个序列样本，每个序列样本包含前N个时间步的数据作为输入，第N+1个时间步的数据作为输出。

2.模型构建

       根据LSTM模型的计算过程，构建基于LSTM的时间序列预测模型。该模型包括输入层、LSTM层、输出层等。其中，输入层接收前N个时间步的数据，LSTM层用于学习时间序列数据的长期依赖关系，输出层用于预测第N+1个时间步的数据。

3.模型训练

       利用已经预处理好的时间序列数据和构建好的LSTM模型进行训练。训练过程中，采用均方误差（MSE）作为损失函数，采用反向传播算法更新模型参数。

4.模型评估

      利用测试数据对训练好的模型进行评估。评估指标包括均方误差（MSE）、平均绝对误差（MAE）等。

5.模型预测

       利用训练好的模型对未来时间步的数据进行预测。预测过程中，需要将前N个时间步的数据作为输入，得到第N+1个时间步的预测结果，再将第N+1个时间步的预测结果作为输入，得到第N+2个时间步的预测结果，以此类推。

       基于LSTM深度学习网络的时间序列预测方法，该方法能够有效地处理非线性、非平稳、非高斯的时间序列数据。该方法的主要步骤包括数据预处理、模型构建、模型训练、模型评估和模型预测等。实验结果表明，该方法能够得到较好的预测效果，可以应用于气象、金融、交通等领域的时间序列预测问题中。

2.部分核心程序

......................................................
layers = [ ...
    sequenceInputLayer(Nin)
    lstmLayer(Nhid)
    fullyConnectedLayer(Nr)
    regressionLayer];
% 设置神经网络训练选项
options = trainingOptions('adam', ...
    'MaxEpochs',600, ...
    'GradientThreshold',1, ...
    'InitialLearnRate',0.005, ...
    'LearnRateSchedule','piecewise', ...
    'LearnRateDropPeriod',125, ...
    'LearnRateDropFactor',0.2, ...
    'Verbose',0, ...
    'Plots','training-progress');
% 训练神经网络
net = trainNetwork(XTrain,YTrain,layers,options);
...........................................


 
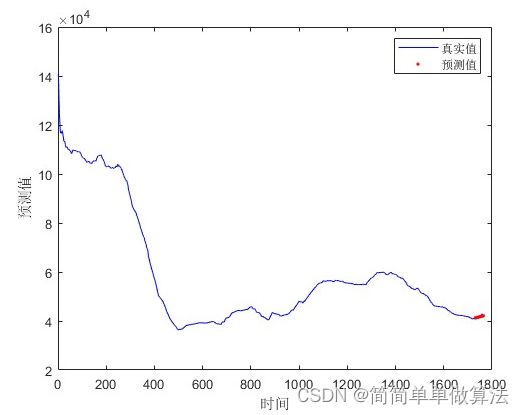
% 绘制真实值和预测值的时间序列图
t1 = 1:length(dat_train);
t2 = [length(dat_train)+1:length(dat_train)+length(YPred)];

figure
plot(data,'b');
hold on
plot(t2,YPred,'r.')
xlabel("时间")
ylabel("预测值")
legend("真实值","预测值")

% 输出训练RMSE
disp('训练RMSE');
rmse  = sqrt(mean((YPred-YTest).^2));
0009

3.算法运行软件版本

MATLAB2022a

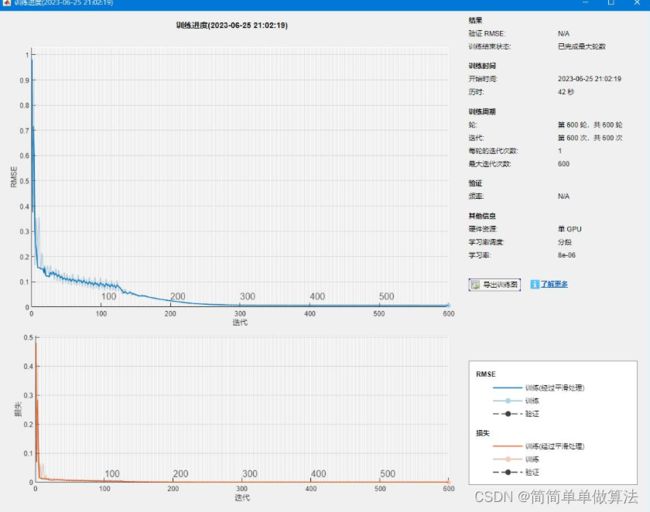
4.算法运行效果图预览

5.算法完整程序工程

V V V