动态规划入门第1课
1、从计数到选择 ---- 递推与DP(动态规划)
2、从递归到记忆 ---- 子问题与去重复运算
3、动态规划的要点
第1题 网格路1(grid1)
小x住在左下角(0,0)处,小y在右上角(n,n)处。小x需要通过一段网格路才能到小y家。每次,小x可以选择下面任意一个方向前进:
-
右方:从(x,y)到点(x+1,y);
-
上方:从(x,y)到点(x,y+1);
-
右上方:从(x,y)到点(x+1,y+1)。
问小x有多少种走法到达小y家。
输入格式
一行,一个整数n。1 ≤ n ≤ 500
输出格式
你的答案除以1 000 000 007的余数。
输入/输出例子1
输入:
2
输出:
13
样例解释
无
代码奉上:
#include
using namespace std;
long long n;
long long f[505][505];
const long long mod=1000000007;
int main(){
scanf("%lld",&n);
n+=1; //题目中是(0,0)到(n,n),我为了防止数组越界,要+1,也会方便很多。
f[0][0]=1; //初始化。
for(long long i=1;i<=n;i++)
for(long long j=1;j<=n;j++)
f[i][j]=(f[i-1][j-1]%mod+f[i-1][j]%mod+f[i][j-1]%mod)%mod; //动态转移方程。
printf("%d\n",f[n][n]%mod);
return 0;
}
小问题推导大问题 ------ 子问题概念
- 测试2
第1题 好的序列(seq)
一个长为k的序列b1, b2, ..., bk (1 ≤ b1 ≤ b2 ≤ ... ≤ bk ≤ n),如果对所有的 i (1 ≤ i ≤ k - 1),满足bi | bi+1,那么它就是好的序列。这里a | b表示a是b的因子,或者说a能整除b。
给出n和k,求长度为k的好的序列有多少个。
输入格式
一行,两个整数n,k。1 ≤ n,k ≤ 2000
输出格式
你的答案除以1 000 000 007的余数。
输入/输出例子1
输入:
3 2
输出:
5
样例说明
[1, 1], [2, 2], [3, 3], [1, 2], [1, 3]。
样例解释
无
代码奉上:
#include
#include
#define rr register
using namespace std;
int cwh=1000000007,n,k,f[2005][2005],ans;//用cwh表示1000000007更方便。
int main()
{
scanf("%d%d",&n,&k);
for(rr int i=1;i<=n;i++)
f[1][i]=1;//赋值
for(rr int i=1;i<=k;i++)//长度
for(rr int j=n;j>0;j--)
for(rr int k=1;k<=n/j;k++)//倍数
f[i][j*k]=(f[i][j*k]+f[i-1][j])%cwh;//方程
for(rr int i=1;i<=n;i++)
ans=(ans+f[k][i])%cwh;//求答案
printf("%d",ans);
return 0;
}
小问题推导大问题
两个方向:改进后面;从前面得到;
- 测试3
第1题 卡牌游戏(card)
有三种卡牌,记为A,B,C类型。每轮,小x可以选择的出牌方法有:
-
打出一张A牌;
-
打出一张B牌;
-
打出一张A牌和一张C牌;
-
打出两张B牌和三张C牌。
问小x有多少种方法出完所有的牌。只要有一轮出牌的方法不一样,就算作不同的方法。
输入格式
一行,三个整数a,b,c,依次表示卡牌A,B,C的数量。1 ≤ a,b,c ≤ 15
输出格式
你的答案除以1 000 000 007的余数。
输入/输出例子1
输入:
2 2 3
输出:
3
样例解释
无
代码奉上:
#include
using namespace std;
int a,b,c;
int f[55][55][55];
const int mod=1000000007;
int main(){
cin>>a>>b>>c;
f[0][0][0]=1;
for(int i=0;i<=a;i++){
for(int j=0;j<=b;j++){
for(int k=0;k<=c;k++){ //枚举A,B,C卡牌的数量
if(i>=1){f[i][j][k]+=f[i-1][j][k];f[i][j][k]%=mod;} //DP,记得特判,不然会越界。下同。
if(j>=1){f[i][j][k]+=f[i][j-1][k]%mod;f[i][j][k]%=mod;}
if(i>=1 && k>=1){f[i][j][k]+=f[i-1][j][k-1]%mod;f[i][j][k]%=mod;}
if(j>=2 && k>=3){f[i][j][k]+=f[i][j-2][k-3]%mod;f[i][j][k]%=mod;}
}
}
}
cout< 大问题分解为小问题 ------ 状态概念
小问题推导出大问题 ------- 计算方法;方程
f[ a ][ b ][ c ] =?
- 测试4
第1题 四面体(tetra)
一只蚂蚁从点A出发,每次行动可沿四面体的边来到另外一个点。问n次行动后,蚂蚁回到点A有多少种方法。
输入格式
一行,一个整数n。1 ≤ n ≤ 10^6
输出格式
你的答案除以1 000 000 007的余数。
输入/输出例子1
输入:
2
输出:
3
样例解释
无
代码奉上:
#include
using namespace std;
long long n;
long long f[1000000][6];
const long long mod=1000000007;
int main(){
scanf("%lld",&n);
f[0][1]=1;
for(int i=1;i<=n;i++){
f[i][1]=(f[i-1][2]%mod+f[i-1][3]%mod+f[i-1][4]%mod)%mod;
f[i][2]=(f[i-1][1]%mod+f[i-1][3]%mod+f[i-1][4]%mod)%mod;
f[i][3]=(f[i-1][2]%mod+f[i-1][1]%mod+f[i-1][4]%mod)%mod;
f[i][4]=(f[i-1][2]%mod+f[i-1][3]%mod+f[i-1][1]%mod)%mod;
}
printf("%d\n",f[n][1]);
return 0;
}
状态与阶段
- 测试5
- 第1题 网格取数1
有N*M的方格,每个方格里面有一个数字。你从左上角开始出发,每次可以进入右边一个方格或下面一个方格,不准出界。
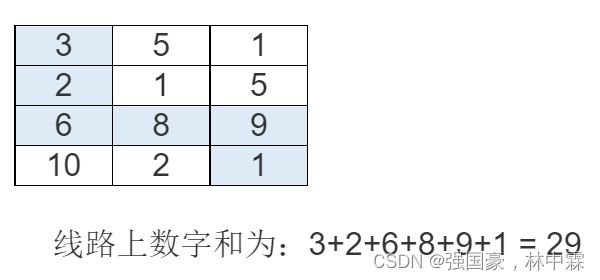
问你选择怎样的线路到达右下角时,线路上的数字和最大?
例如下面是一个4*3的方格,最优的路线如图所示:
输入格式
第1行:2个正整数N和M,范围[2,100]。
下面N行,每行M个整数,每个整数范围[-100,100]
输出格式
一个整数。
输入/输出例子1
输入:
3 3
1 2 3
4 5 6
9 9 9
输出:
32
样例解释
无
代码奉上:
#include
using namespace std;
long long n,m,a[1005][1005],b[1005][1005];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(i==1&&j==1)
b[i][j]=a[i][j];
else if(i==1)
b[i][j]=b[i][j-1]+a[i][j];
else if(j==1)
b[i][j]=b[i-1][j]+a[i][j];
else
b[i][j]=(b[i-1][j]>b[i][j-1])?b[i-1][j]+a[i][j]:b[i][j-1]+a[i][j];
}
}
cout< 总结: