机器学习方法与原则

机器学习方法与原则

评价指标

TODO

训练集、验证集与测试集

训练集与测试集

• 训练集（作业）： 模型可见样本标签，用于训练模型，样本数量有限。
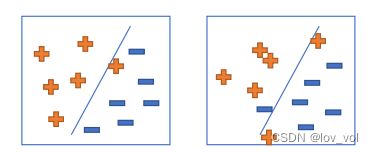
  • 在训练集上表现好的模型， 在其它未见样本上一定表现好么？ 小心过拟合
• 未见样本（所有没做过的题）往往有指数级别或者无穷多个。测试集和训练集都属于未见样本。
• 测试集（考试）： 用于评估模型在可能出现的未见样本上的表现
  • 尽可能与训练集互斥，即测试样本 尽量不在训练集中出现，主要估计泛化能力
  • 估计模型在整个未见样本的表现

训练集与测试集的划分方式

• 随机划分
  • 按比例，例如 9：1、8：2
  • 固定数目，例如测试集从全部样本中采样1w个， 其余为训练集
• 留一划分（leave- one-out）
  • 适用于数据量少的
  • 一个样本做测试，其余样本训练：常用于K近邻
    等算法的性能评估
• 特殊划分
  • 按时间划分（一般是天然有时间序列的， 而且时间很重要）， 例如 1-5月气象数据作训练， 6月气象数据作测试
  • 推荐系统中， 常把每个用户交互序列的最后一个样本作测试， 其余作训练。
  • …

验证集

• 从训练集中额外分出的集合，一般用于超参数的调整
  • 训练轮次、正则化权重、学习率等等
• 为什么不在训练集上调整超参数？过拟合训练集
• 为什么不在测试集上调整超参数？过拟合测试集
  • 针对当前测试集调出的参数可能只在当前测试集上较好
  • 使得测试集结果偏高，不能反映实际在所有未见样本上的效果
  • 类比： 针对某场考试的知识点分布作重点复习，不能准确反映学生对所有知识的掌握程度。
  • 举例： 机器学习竞赛中，针对公开部分的测试数据过度调参，不一定在隐蔽的全部测试数据上表好。

训练集、测试集与验证集

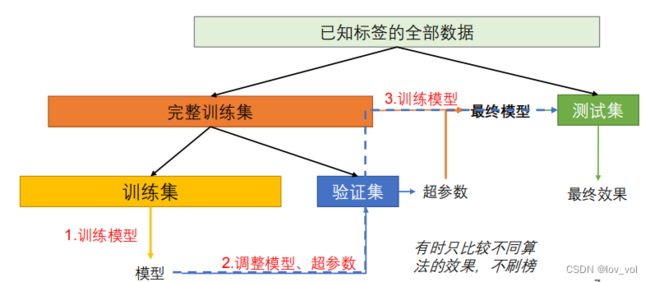
如果知识比较算法，只需要经过训练集和验证集处理就行， 不需要再经过完整训练集处理。

训练示例： 比如测试12月天气数据， 11月作为验证集，1-10月作为训练集， 经过1-10月数据的训练，并在验证集上调参， 确定$A(\alpha ,\beta )$函数好， 再经过完整训练集处理，得出$A^{{}^{\prime }}$, 在测试集上测试。

随机重复实验

问题

• 测试一次就足够了么？

  • 极端情况： 二分类中分类器随机输出，恰好测试集都对了（效果最好？）

• 数据随机性

  • 由 数据集划分带来的评价指标波动，如第一次负例都在下方， 第二次有个负例在上方

• 模型随机性

  • 由模型或学习算法本身带来的评价指标波动
  • 例如：神经网络初始化、训练批次生成 、比如局部最优的方法，起点不同会导致最终不一样，还比如使用到的random

方法

• 数据随机性

  • （数据足够多时）增多测试样本
  • （数据量有限时）重复多次划分数据集

• 模型随机性

  • 更改随机种子重复训练、测试

• 注意： 保持每次得到的评价指标独立同分布（iid）
  比如，第一次取这个好， 第二次就在这个的基础上再取，这样不符合独立同分布

• 报告结果： (多次随机试验的）评价指标的均值$\overline{X}=\frac{1}{n}{\sum }_{i=1}^n{X}_i$

  • 样本标准差（个体离散程度，反映了个体对样本均值的代表性） $S=\sqrt{{\sum }_{i=1}^n\frac{(X_i-\overline{X}{)}^2}{n-1}}$
  • 标准误差（样本均值的离散程度，反映了样本均值对总体均值的代表性）
    $StandardErroroftheMean,SEM=\frac{S}{\sqrt{n}}=\sqrt{{\sum }_{i=1}^n\frac{(X_i-\overline{X}{)}^2}{n(n-1)}}$

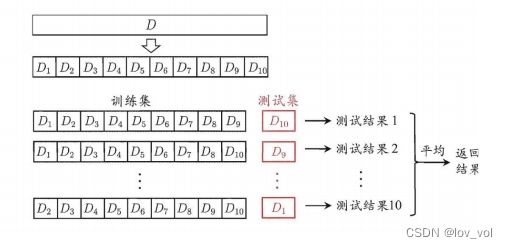
K折交叉验证(K-fold cross validation )

• 随机把数据集分成K个相等大小的不相交子集。
  选出一份作为测试集，一共k种情况， 分别训练， 得出k个测试结果，取平均得出最终结果。
  

优缺点

• 优点： 数据利用率高，适用于数据较少时
• 缺点： 训练集相互有交集，每一轮之间并不满足独立同分布，两轮之间至少k-2组数据相同

其它

• 增大K，一般情况下：

  • 所评估的模型效果偏差（bias）下降
  • 所估计的模型效果方差（variance）上升
  • 计算代价上升，更多轮次、训练集需求更大

• K 一般取5、10

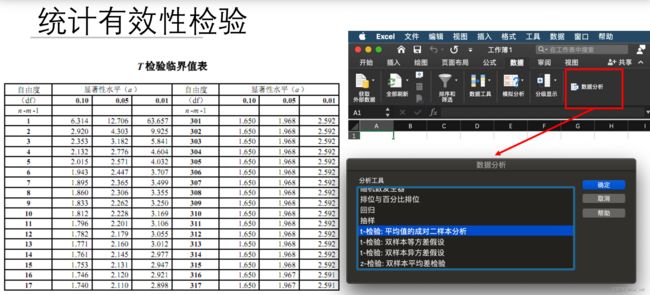
统计有效性检验

问题

假设的评估检验： 问题1

• 效果估计
  • 给一个假设在有限量数据上的准确率
  • 该准确率是否能够准确估计其它未见数据上的效果
    

假设的评估检验：问题2

• h₁ 在数据的一个样本集上表现优于h₂
• h₁总体上更好的概率有多大
  

解答

估计假设准确率 -Q1.1 解答

用到后面二项分布的知识

如何对一个假设h 在来自同一分布的未见样本上的准确率作出最好的估计？

**n个随机样本(测试集上的)中有r个被误分类的概率–二项分布 $P(r)=\frac{n!}{r!(n-r)!}{p}^r(1-p{)}^{n-r}$

$erro{r}_D(h)=p$, 真实错误率是p
样本错误率，$erro{r}_s(h)=\frac{r}{n}$ ，n次错了r次， s代表样本（sample）

$E[r]=np,E[erro{r}_S(h)]=E[\frac{r}{n}]=\frac{np}{n}=p=erro{r}_D(h)$ 样本错误率的期望值=真实错误率，也就是进行很多次后，样本错误率=真实错误率

${\sigma }_{erro{r}_s(h)}=\frac{{\sigma }_r}{n}=\frac{\sqrt{np(1-p)}}{n}=\sqrt{\frac{erro{r}_S(h)(1-erro{r}_S(h))}{n}}$

$测试集样本数n=100,错了r=12个样本错误率是12\%，则标准差\sigma =3.2\%$
$测试集样本数n=25,错了r=3个样本错误率是12\%，则标准差\sigma =6.5\%$

估计的两个重要性质

• 估计偏差 （Bias）
  • 如果 S 是训练集, error_S(h) 是有偏差的（偏乐观），
    $bias\equiv E[errorS(h)]-errorD(h)$
  • 对于无偏估计(bias =0), h(训练集的模型） 和 S（测试集样例） 必须独立不相关地产生
    → 不要在训练集上测试！
• 估计方差 （Varias）
  • 即使是S 的无偏估计, $errorS(h)$可能仍然和 $erro{r}_D(h)$ 不同
    • E.g. 之前的例子 (3.2% vs. 6.5%)
  • 需要选择无偏的且有最小方差的估计

估计假设准确率 – Q1.2解答

准确率的估计可能包含多少错误？
($erro{r}_S(h)对erro{r}_D(h)的估计有多好?$)

用到后面的正态知识
$均值\mu$其实就是样本的错误率

• 如果如果满足以下条件，估计更准确：
  • (测试集）S 包含 n >= 30个样本, 与h独立产生，且每个样本独立采样
• 那么有大约95%的概率**(ℎ)**落在区间 $erro{r}_D(h)\underline{+}1.96\sqrt{\frac{erro{r}_D(h)(1-erro{r}_D(h))}{n}}$
• 等价于,$erro{r}_D$落在区间$erro{r}_S(h)\underline{+}1.96\sqrt{\frac{erro{r}_D(h)(1-erro{r}_D(h))}{n}}$ (用到后面正态的等价，y: $\mu \underline{+}z\sigma$ => $\mu :y\underline{+}z\sigma$
• 近似等于，$erro{r}_S(h)\underline{+}1.96\sqrt{\frac{erro{r}_S(h)(1-erro{r}_S(h))}{n}}$ (无偏估计下，期望E(error_s)=error_D)

问题1解答总结

• 问题设定:

  • S(测试集）: n 随机独立样本, 且独立于假设 h(即bias=0)
  • n >= 30 & h 有 r 个错误

• **真实错误率$erro{r}_D$**落在以下区间有N% 置信度
  $erro{r}_S(h)\underline{+}{z}_N\sqrt{\frac{erro{r}_S(h)(1-erro{r}_S(h))}{n}}$
  

  推导置信区间的一般方法

  • 一般地，
    • 确定需要估计的变量 p, e.g. $erro{r}_D(h)$
    • 确定估计量Y (偏差, 方差), e.g. $erro{r}_S(h)$
      • 希望 : 小方差, 无偏估计
    • 确定Y 的分布 D (包括均值 & 方差)
    • 确定N% 置信区间 (L…U) •
      • 可能有 L=-∞ or U=∞
      • E.g. （对于正态分布）利用 $z_n$ 表查询相关值

• 也可应用在其他问题上

中心极限定理

• 简化了求解置信区间的过程

• 问题设定

  • 独立同分布Independent, identically distributed (iid)
    的随机变量$Y_1,...,Y_n$
  • 未知分布, 有均值 μ 和有限方差 σ2
  • 估计均值: $\overline{Y}\equiv \frac{1}{n}{\sum }_{i=1}^n{Y}_i$

• 中心极限定理

  • $\overline{Y}$服从正态分布 (n →∞)
  • 均值 $\mu$ , 方差${\sigma }^2/n$
  • 可以被归一化到标准正态分布，即$\mu =0,\sigma =1$

• 样本均值$\overline{Y}$ 的分布

  • 是已知的
  • 即使 $Y_i$ 的分布是未知的
  • 可以用来确定的$Y_i$均值方差

• 提供了估计的基础

  • 估计量的分布
  • 一些样本的均值

问题2的解答

• h1 在数据的一个样本集上表现优于 h2
  • h1 总体上更好的概率有多大？
    假设之间的差异
    

假设间的差异

• 在样本集合$S_1$ ($n_1$个随机样本)上测试$h_1$, 在$S_2(n_2)$上测试$h_2$
• 选择要估计的参数 $d\equiv erro{r}_D(h1)-erro{r}_D(h2)$
• 选择估计量
  • 无偏的 $\hat{d}\equiv erro{r}_{S_1}(h1)-erro{r}_{S_2}(h2)$
• 确定估计量 $\hat{d}$ 所服从的概率分布
  • $erro{r}_{S_1}(h1)$ , $erro{r}_{S_2}(h2)$ 近似服从正态分布
  • $\hat{d}$ 也近似正态分布
    • 均值 = d
    • 方差: 加和
      ${\sigma }_{\hat{d}}\approx \sqrt{\frac{erro{r}_{S_1}(h_1)(1-erro{r}_{S_1}(h_1))}{n_1}+\frac{erro{r}_{S_2}(h_2)(1-erro{r}_{S_2}(h_2))}{n_2}}$

证明正态分布和也是正态分布: http://en.wikipedia.org/wiki/Sum_of_normally_distributed_random_variables

• 确定区间（L,U)满足N%的概率落在区间
  $\hat{d}\underline{+}{z}_N\sqrt{\frac{erro{r}_{S_1}(h_1)(1-erro{r}_{S_1}(h_1))}{n_1}+\frac{erro{r}_{S_2}(h_2)(1-erro{r}_{S_2}(h_2))}{n_2}}$

假设检验

• 某些陈述可能是真的概率
  • E.g. 例如 $e_D(h_1)>e_D(h_2)$的概率
• 例子($n_1=n_2=100$)
  • $错误率e_{S_1}(h_1)=0.3,错误率e_{S_2}(h_2)=0.2,求e_D(h_1)>e_D(h_2)$的概率
  1. $\hat{d}\equiv erro{r}_{S_1}(h_1)-erro{r}_{S_2}(h_2)$
  2. $d\equiv erro{r}_{D_1}(h_1)-erro{r}_{D_2}(h_2)$
  3. 给定$\hat{d}=0.1,求e_D(h_1)>e_D(h_2)$的概率
  4. 给定$\hat{d}=0.1,求d>0$的概率， 也就是d + 0.1 > 0.1的概率，也就是d + 0.1 > $\hat{d}$
  5. $\hat{d}$在区间d + 0.1 > $\hat{d}$的概率
     • 注意： d是$\hat{d}$概率分布的均值
  6. $\hat{d}$在区间$\hat{d}<{\mu }_{\hat{d}}+0.1$的概率
     $\mu \underline{+}{z}_n\sigma$

统计有效性检验： z检验（举例1）

• z 检验适用于（独立同分布）
• $n_1=n_2=100,ac{c}_{S_1}(h_1)=0.3,ac{c}_{S_2}(h_2)=0.2$
• 则$\hat{d}\equiv ac{c}_{S_1}(h_1)-ac{c}_{S_2}(h_2)=0.1$
• 求$d\equiv ac{c}_{D_1}(h_1)-ac{c}_{D_2}(h_2)>0$的置信度
• 即求$\hat{d}<d+0.1$的概率（d>0,两边同时+0.1, 用$\hat{d}=0.1$推出）
• 又有${\sigma }_{\hat{d}}\approx \sqrt{\frac{erro{r}_{S_1}(h_1)(1-erro{r}_{S_1}(h_1))}{n_1}+\frac{erro{r}_{S_2}(h_2)(1-erro{r}_{S_2}(h_2))}{n_2}}=0.061$
• 则$\hat{d}<d+0.1\to \hat{d}<d+1.64{\sigma }_{\hat{d}}$ （是由 $\hat{d}<d+Z_n\sigma$, $Z_n=0.1/0.061\approx 1.64$推出)
• 即$Z_N=1.64$, 查正态分布表可知，双边置信度为90%,
• 则单边置信度95%
• 即$ac{c}_{D_1}(h_1)>ac{c}_{D_2}(h_2)$的置信度为95%

统计有效性检验： z检验（举例1）

• z 检验适用于（独立同分布）
• $n_1=n_2=30,ac{c}_{S_1}(h_1)=0.3,ac{c}_{S_2}(h_2)=0.2$
• 则$\hat{d}\equiv ac{c}_{S_1}(h_1)-ac{c}_{S_2}(h_2)=0.1$
• 求$d\equiv ac{c}_{D_1}(h_1)-ac{c}_{D_2}(h_2)>0$的置信度
• 即求$\hat{d}<d+0.1$的概率（d>0,两边同时+0.1, 用$\hat{d}=0.1$推出）
• 又有${\sigma }_{\hat{d}}\approx \sqrt{\frac{erro{r}_{S_1}(h_1)(1-erro{r}_{S_1}(h_1))}{n_1}+\frac{erro{r}_{S_2}(h_2)(1-erro{r}_{S_2}(h_2))}{n_2}}=0.111$
• 则$\hat{d}<d+0.1\to \hat{d}<d+0.90{\sigma }_{\hat{d}}$ （
• 即$Z_N=0.90$, 查正态分布表可知，双边置信度为68%,
• 则单边置信度84%
• 即$ac{c}_{D_1}(h_1)>ac{c}_{D_2}(h_2)$的置信度为84%

统计有效性检验：t检验

z检验只适合独立同分布， 非独立同分布可以使用t检验
交叉验证如果测试题不同可以用z检验，否则只能用t检验

• 记模型$h_1$的$n_1$次重复实验结果为$x_{11},x_{12},\dots ,x_{1n_1}$
  ${\overline{x}}_1=\frac{1}{n_1}{\sum }_{i=1}^{n_1}{x}_{1i},s_1^2=\frac{1}{n_1-1}{\sum }_{i=1}^{n_1}(x_{1i}-{\overline{x}}_1{)}^2$
• 记模型$h_2$的$n_2$次重复实验结果为$x_{21},x_{22},\dots ,x_{2n_2}$
  ${\overline{x}}_2=\frac{1}{n_2}{\sum }_{i=1}^{n_2}{x}_{2i},s_2^2=\frac{1}{n_2-1}{\sum }_{i=1}^{n_2}(x_{2i}-{\overline{x}}_2{)}^2$
• 在样本量及方差均不相等的假设下有
  • 检验量$t=({\overline{x}}_1-{\overline{x}}_2)/\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}$, 自由度$df=(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}{)}^2/(\frac{s_1^4}{n_1^2(n_1-1)}+\frac{s_2^4}{n_2^2(n_2-1)})$
• 若1 = 2 = 且 $d_i=x_{1i}-x_{2i}$独立且来自正态分布
• 可采用配对t检验（paired t-test），例如两组结果测试集依次相同时
• 即两个模型在同样划分的交叉验证或同样测试集的重复对比实验
  检验量$t=({\overline{x}}_1-{\overline{x}}_2)/\sqrt{\frac{{\sum }_{i=1}^n(d_i-\overline{d}{)}^2}{n(n-1)}}$, 自由度为 − 1
  • 根据检验量和自由度查t分布表可得置信度(类似根据$z_N$查正态分布表)

统计有效性

统计有效性检验(总结）

• 比较算法A和B的优劣
  • 准确率均值高就一定好？有随机性
  • A比B高多少才能有把握说A算法更好？显著性检验(N > 90% 95 % 99% 一般是选择大于99%
• 随机变量的样本个数较多时(一般>30)： z检验(利用中心极限定理)
  • 一般用于单次评测，随机变量为每个测试样本的对错
• 随机变量的样本个数较少时(一般<=30)：t检验
  • 一般用于多次评测如重复实验，随机变量为每次测试集上的指标

小结

• 评价指标：回归任务， 分类任务， 特定任务
• 训练集、验证集与测试集：随机划分， 留一划分，特殊划分
• 随机重复实验
• K折交叉验证
• 统计有效性检验：z检验，t检验

##抽样理论基础（Sample theory）

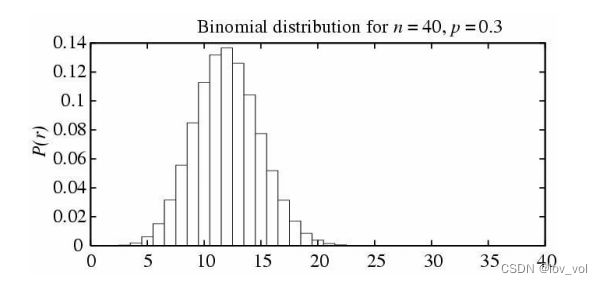
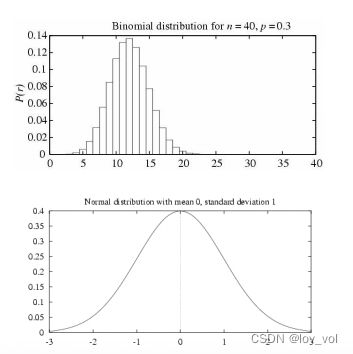
二项分布(Binomial Distribution)

• 伯努利实验
  • 只有 2 种输出:
    成功概率: $p$，失败概率: $q=1-p$
  • 用随机变量 $X$ 记录成功的次数
• 伯努利分布:
  • 抛硬币: 正面朝上的概率为 $p$, 抛 $n$ 次, 观察到 $r$ 次正面朝上
  • 若计 $X$~ $B(n,p)$， $P_r(X=r)=P(r)$ ，则
    $P(r)=\frac{n!}{r!(n-r)!}{p}^r(1-p{)}^{n-r}$
    

二项分布的应用场景

• 两个可能的输出 (成功/失败) ($Y=0或Y=1$)
• 每次尝试成功的概率相等 $Pr(Y=1)=p,其中p是一个常数$
• $n$ 次独立尝试
  • 随机变量 $Y_1,...,Y_n$
  • iid (independent identically distribution，独立同分布)
  • R: 随机变量, n 次尝试中 $Y_i=1$的次数,
• $P_r(R=r)$ ~ 二项分布
• 平均 (期望值): $E[R],\mu$
  • 二项分布: $\mu =np$
• 方差: $Var[R]=E[(R-E[R]{)}^2],{\sigma }^2(标准差\sigma )$
  • 二项分布: ${\sigma }^2=np(1-p)$
    

置信区间（confidence interval）

• 定义
  • 参数p 的N %置信区间是一个以N %的概率包含p 的区间, N% : 置信度
    ✓ 90.0%的置信度 ，年龄：[12, 24], p是年龄
    ✓ 99.9%的置信度，年龄：[3, 60]
    如 95%的错误率在12%～17%之间

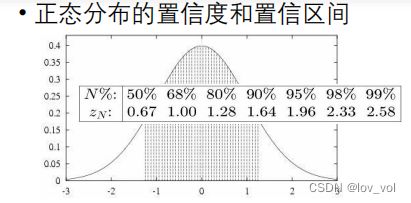
置信度与置信区间

• 如何得到置信区间?
  • 坏消息: 对二项分布来说很难
  • 好消息: 对正态分布来说很简单
    • 通过正态分布的某个区间（面积）来获得
      
• 指标y有$N\%$ 的可能性落在区间$\mu \underline{+}{Z}_N\sigma$
• 等价于, 均值 $\mu$ 有$N\%$ 的可能性落在区间$y\underline{+}{z}_N\sigma$
  $均值\mu$其实就是样本的错误率

正态分布

• 正态分布的概率密度函数
  $p(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{1}{2}(\frac{x-\mu }{\sigma }{)}^2}$
  

正态分布&二项分布

• 对于足够大的采样大小
  二项分布 ---->>>可以通过正态分布近似表示
• 经验法则: n>30, np(1-p)> 5 同时满足