算法与数据结构（十九）回溯法总结（子集&组合）

1. DFS 和回溯算法区别

DFS 是一个劲的往某一个方向搜索，而回溯算法建立在 DFS 基础之上的，但不同的是在搜索过程中，达到结束条件后，恢复状态，回溯上一层，再次搜索。因此回溯算法与 DFS 的区别就是有无状态重置

2.何时使用回溯算法

当问题需要 “回头”，以此来查找出所有的解的时候，使用回溯算法。即满足结束条件或者发现不是正确路径的时候(走不通)，要撤销选择，回退到上一个状态，继续尝试，直到找出所有解为止

3.怎么样写回溯算法(从上而下，※代表难点，根据题目而变化)

① 画出递归树，找到状态变量(回溯函数的参数)，这一步非常重要※
② 根据题意，确立结束条件
③ 找准选择列表(与函数参数相关),与第一步紧密关联※
④ 判断是否需要剪枝
⑤ 作出选择，递归调用，进入下一层
⑥ 撤销选择

4.回溯问题的类型

这里先给出，我总结的回溯问题类型，并给出相应的 leetcode题目(一直更新)，然后再说如何去编写。特别关注搜索类型的，搜索类的搞懂，你就真的搞懂回溯算法了,，是前面两类是基础，帮助你培养思维

类型	题目链接
子集、组合	子集、子集 II、组合、组合总和、组合总和 II
全排列	全排列、全排列 II、字符串的全排列、字母大小写全排列
搜索	解数独、单词搜索、N皇后、分割回文串、二进制手表

注意：子集、组合与排列是不同性质的概念。子集、组合是无关顺序的，而排列是和元素顺序有关的，如 [1，2] 和 [2，1] 是同一个组合(子集)，但 [1,2] 和 [2,1] 是两种不一样的排列！！！！因此被分为两类问题

5. 回到子集、组合类型问题上来(ABC 三道例题)

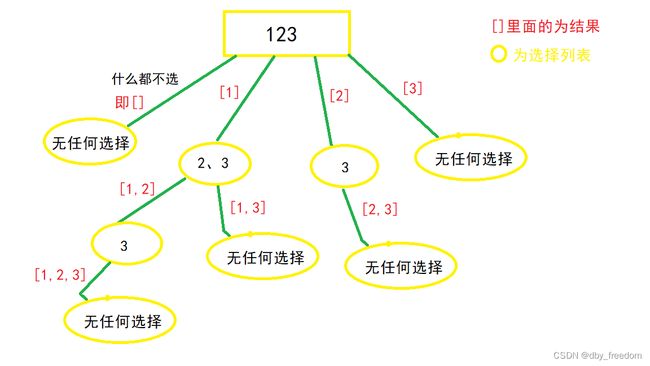
A、 子集 - 给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
解题步骤如下

①递归树

观察上图可得，选择列表里的数，都是选择路径(红色框)后面的数，比如[1]这条路径，他后面的选择列表只有"2、3"，[2]这条路径后面只有"3"这个选择，那么这个时候，就应该使用一个参数start，来标识当前的选择列表的起始位置。也就是标识每一层的状态，因此被形象的称为"状态变量",最终函数签名如下

C++

//nums为题目中的给的数组
//path为路径结果，要把每一条 path 加入结果集
void backtrack(vector<int>nums,vector<int>&path,int start)

②找结束条件
此题非常特殊，所有路径都应该加入结果集，所以不存在结束条件。或者说当 start 参数越过数组边界的时候，程序就自己跳过下一层递归了，因此不需要手写结束条件,直接加入结果集

C++

**res为结果集，是全局变量vector<vector<int>>res,到时候要返回的
res.push_back(path);//把每一条路径加入结果集

③找选择列表
在①中已经提到过了，子集问题的选择列表，是上一条选择路径之后的数,即

C++

for(int i=start;i<nums.size();i++)

④判断是否需要剪枝
从递归树中看到，路径没有重复的，也没有不符合条件的，所以不需要剪枝

⑤做出选择(即for 循环里面的)
C++

void backtrack(vector<int>nums,vector<int>&path,int start)
{
    for(int i=start;i<nums.size();i++)
    {
        path.push_back(nums[i]);//做出选择
        backtrack(nums,path,i+1);//递归进入下一层，注意i+1，标识下一个选择列表的开始位置，最重要的一步
    }
}

⑤撤销选择
整体的 backtrack 函数如下

C++

void backtrack(vector<int>nums,vector<int>&path,int start)
{
    res.push_back(path);
    for(int i=start;i<nums.size();i++)
    {
        path.push_back(nums[i]);//做出选择
        backtrack(nums,path,i+1);//递归进入下一层，注意i+1，标识下一个选择列表的开始位置，最重要的一步
        path.pop_back();//撤销选择
    }
}

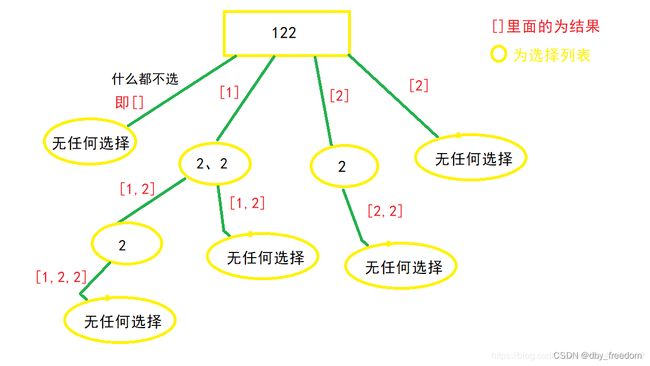
B、子集 II(剪枝思想)–问题描述:
给定一个可能 包含重复元素 的整数数组 nums，返回该数组所有可能的子集（幂集）。
输入: [1,2,2]
输出:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]

解题步骤 ①递归树

可以发现，树中出现了大量重复的集合，②和③和第一个问题一样，不再赘述，我们直接看第四步

④判断是否需要剪枝，需要先对数组排序，使用排序函数 sort(nums.begin(),nums.end())
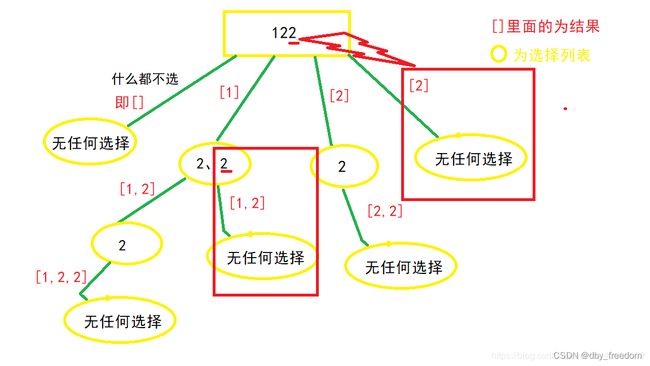
显然我们需要去除重复的集合，即需要剪枝，把递归树上的某些分支剪掉。那么应去除哪些分支呢？又该如何编码呢？

观察上图不难发现，应该去除当前选择列表中，与上一个数重复的那个数，引出的分支，如 “2，2” 这个选择列表，第二个 “2” 是最后重复的，应该去除这个 “2” 引出的分支

(去除图中红色大框中的分支)

编码呢，刚刚说到是 “去除当前选择列表中，与上一个数重复的那个数，引出的分支”，说明当前列表最少有两个数，当i>start时，做选择的之前，比较一下当前数，与上一个数 (i-1) 是不是相同，相同则 continue,

C++

void backtrack(vector<int>& nums,vector<int>&path,int start)
    {
        res.push_back(path);
        for(int i=start;i<nums.size();i++)
        {
            if(i>start&&nums[i]==nums[i-1])//剪枝去重
                continue;
        }
    }

⑤做出选择
C++

void backtrack(vector<int>& nums,vector<int>&path,int start)
    {
        res.push_back(path);
        for(int i=start;i<nums.size();i++)
        {
            if(i>start&&nums[i]==nums[i-1])//剪枝去重
                continue;
            temp.push_back(nums[i]);
            backtrack(nums,path,i+1);
        }
    }

⑥ 撤销选择
整体的backtrack函数如下

C++

** sort(nums.begin(),nums.end());
void backtrack(vector<int>& nums,vector<int>&path,int start)
    {
        res.push_back(path);
        for(int i=start;i<nums.size();i++)
        {
            if(i>start&&nums[i]==nums[i-1])//剪枝去重
                continue;
            temp.push_back(nums[i]);
            backtrack(nums,path,i+1);
            temp.pop_back();
        }
    }

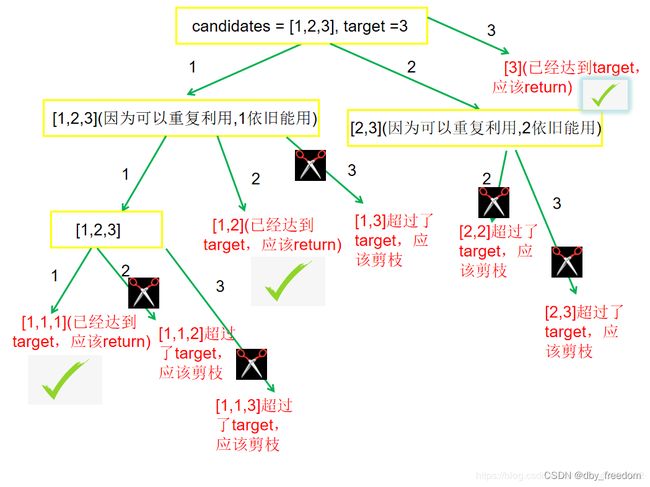
C、组合总和 - 问题描述
给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
输入: candidates = [1,2,3], target = 3,
所求解集为:
[
[1,1,1],
[1,2],
[3]
]

解题步骤 ①递归树

(绿色箭头上面的是路径，红色框[]则为结果，黄色框为选择列表)
从上图看出，组合问题和子集问题一样，1,2 和 2,1 `是同一个组合，因此 需要引入start参数标识，每个状态中选择列表的起始位置。另外，每个状态还需要一个 sum 变量，来记录当前路径的和，函数签名如下

C++

void backtrack(vector<int>& nums,vector<int>&path,int start,int sum,int target)

②找结束条件
由题意可得，当路径总和等于 target 时候，就应该把路径加入结果集，并 return

C++

 if(target==sum)
        {
            res.push_back(path);
            return;
        }

③找选择列表
C++

 for(int i=start;i<nums.size();i++)

④判断是否需要剪枝
从①中的递归树中发现，当前状态的sum大于target的时候就应该剪枝，不用再递归下去了

C++

   for(int i=start;i<nums.size();i++)
        {
            if(sum>target)//剪枝
                continue;
        }

⑤做出选择
题中说数可以无限次被选择，那么 i 就不用 +1 。即下一层的选择列表，从自身开始。并且要更新当前状态的sum

C++

   for(int i=start;i<nums.size();i++)
        {
            if(sum>target)
                continue;
            path.push_back(nums[i]);
            backtrack(nums,path,i,sum+nums[i],target);//i不用+1(重复利用)，并更新当前状态的sum
        }

⑥撤销选择
整体的 backtrack 函数如下

C++

void backtrack(vector<int>& nums,vector<int>&path,int start,int sum,int target)
{
   for(int i=start;i<nums.size();i++)
        {
            if(sum>target)
                continue;
            path.push_back(nums[i]);
            backtrack(nums,path,i,sum+nums[i],target);//更新i和当前状态的sum
            pacht.pop_back();
        }
}

总结：子集、组合类问题，关键是用一个 start 参数来控制选择列表！！最后回溯六步走：

①画出递归树，找到状态变量(回溯函数的参数)，这一步非常重要※
②根据题意，确立结束条件
③找准选择列表(与函数参数相关),与第一步紧密关联※
④判断是否需要剪枝
⑤作出选择，递归调用，进入下一层
⑥撤销选择

注：该文转载改变自，仅用于自身总结及学习交流使用：https://leetcode-cn.com/problems/subsets/solution/c-zong-jie-liao-hui-su-wen-ti-lei-xing-dai-ni-gao-/