岭回归和LASSO回归模型（简记Logistic回归分类模型）

线性回归模型的参数估计得到的前提是变量构成的矩阵可逆。在实际问题中，常出现的问题：

• 可能会出现自变量个数多于样本
• 自变量间存在多重共线性的情况

为解决这类问题，可基于线性回归模型扩展的回归模型：岭回归和LASSO回归模型¹进行处理。最后，对Logistic模型的特点做一简记。

一、岭回归模型

在线性回归模型的目标函数之上添加一个 L2 的正则项（也称为惩罚项），进而使得模型的回归系数有解。
$\lambda$ 是 L2 正则项平方的系数，用来平衡模型的方差（回归系数的方差）和偏差（真实值与预测值之间的差异）

目标函数加上L2正则项的示意图

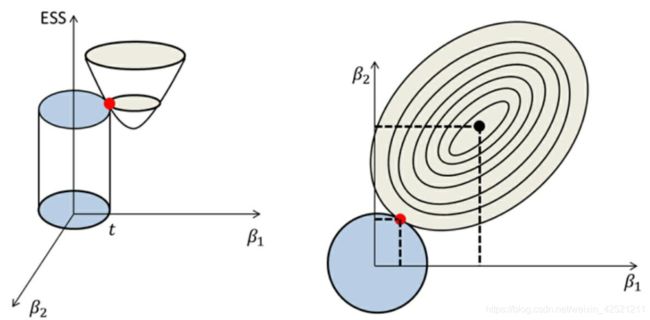
上图的示意比常见的示意图应该更好理解。抛物面与圆面的交点很难发生在轴上，即某个变量的回归系数 $\beta$ 为0，所以岭回归模型并不能从真正意义上实现变量的选择。

1 λ 值的确定

关于λ值的确定，通常可以使用两种方法：

• 一种是可视化方法
• 另一种是交叉验证法。

1.1 可视化方法确定 λ 值

通过绘制不同的λ值和对应回归系数的折线图确定合理的λ值。一般而言，当回归系数随着λ值的增加而趋近于稳定的点时就是所要寻找的λ值。
在Python中，可以使用sklearn子模块linear_model中的Ridge类实现模型系数的求解。

Ridge(
alpha=1.0, # 用于指定lambda值的参数，默认该参数为1。
fit_intercept=True, # bool类型参数，是否需要拟合截距项，默认为True
normalize=False, # bool类型参数，建模时是否需要对数据集做标准化处理，默认为False
copy_X=True, # bool类型参数，是否复制自变量X的数值，默认为True
max_iter=None, # 用于指定模型的最大迭代次数
tol=0.001, # 用于指定模型收敛的阈值
solver=‘auto’, # 用于指定模型求解最优化问题的算法，默认为’auto’，表示模型根据数据集自动选择算法
random_state=None # 用于指定随机数生成器的种子
)

# 导入第三方模块
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn.linear_model import Ridge
import warnings
warnings.filterwarnings("ignore")   # 忽略警告信息输出

# 读取数据
bingdata = pd.read_excel(r'diabetes.xlsx',sep='')
# 选择自变量、因变量
X,y = bingdata.ix[:,2:-1],bingdata.ix[:,-1]
# 将数据集拆分为训练集、测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size=0.2,random_state=123)

# 构造不同的 lambda值
lambds = np.logspace(-5,2,200)
# 构造空列表，用于存储模型的偏回归系数
ridge_coffs = []
# 求解不同lambda对应的系数值
for lambd in lambds:
    ridge = Ridge(alpha=lambd,normalize=True)
    ridge.fit(X_train,y_train)
    ridge_coffs.append(ridge.coef_)

# 绘制lambda 的对数与回归系数的关系
# 设置绘图风格
plt.style.use('seaborn')
# 为了画图中文可以正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] #指定默认字体
plt.rcParams['axes.unicode_minus'] = False  #解决保存图像时负号'-'显示为方块的问题

plt.plot(lambds,ridge_coffs)
# 对x轴做对数处理
plt.xscale('log')
# 设置x轴和y轴标签
plt.xlabel('Log($\lambda$)')
plt.ylabel('Cofficients')
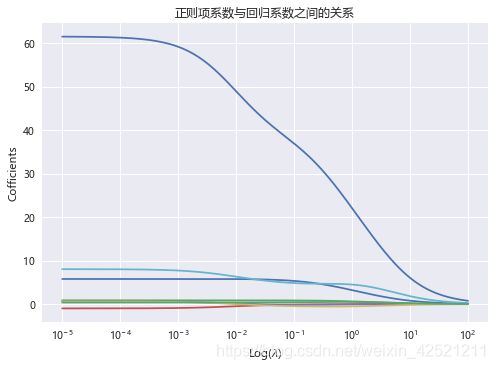
plt.title('正则项系数与回归系数之间的关系')
# 显示图形
plt.show()

使用plotly_express模块可视化，让图表好看点，并且可以互动。

# 加载模块
import plotly_express as px  

# 正则项系数与回归系数之间的关系
p_lam = [lambds] * 8
p_lam = pd.Series(pd.DataFrame(p_lam).values.ravel())
c_s = pd.DataFrame(ridge_coffs,columns=['c'+str(i) for i in range(1,9)])
c_res = pd.Series()
for i in range(8):
    temp = pd.Series(c_s['c'+str(i+1)])
    temp.index=len(lambds)*['c'+str(i+1)]
    c_res = pd.concat([c_res,temp])
c_res = pd.DataFrame(c_res)
c_res = c_res.reset_index()
xy_df= pd.concat([p_lam,c_res],axis=1)
xy_df.columns =['lambda','coef','coef_values']
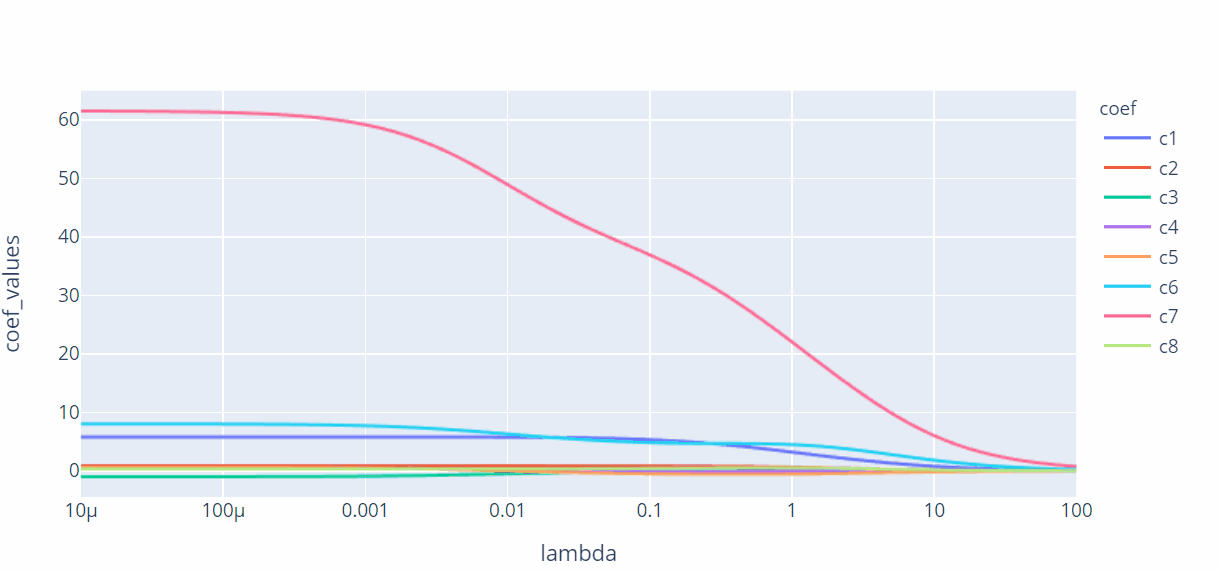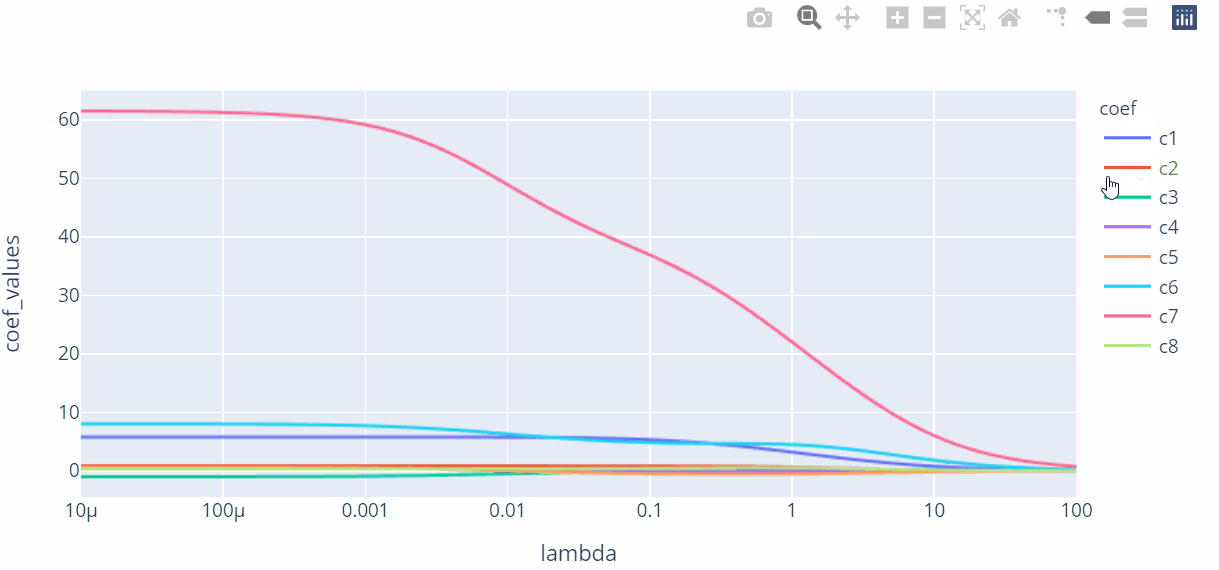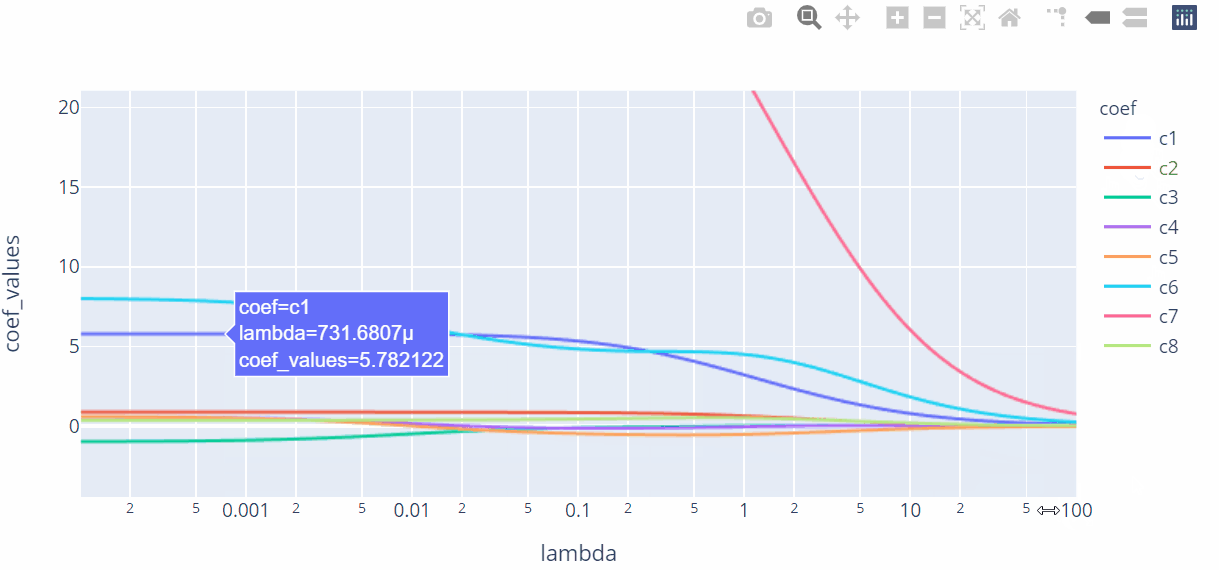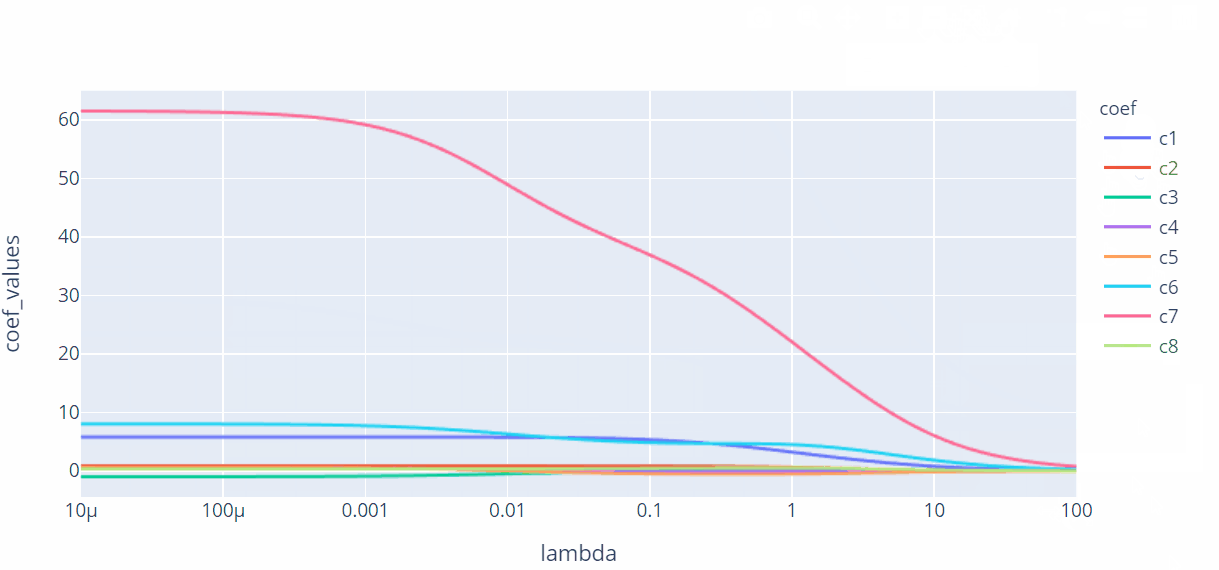
px.line(xy_df,x="lambda",y='coef_values',log_x=True,color='coef',height=400,width=600)

上图展现了不同的λ值与回归系数之间的折线图，图中的每条折线代表了不同的系数，对于比较突出的喇叭形折线，一般代表该变量存在多重共线性。

按照λ值的选择标准，发现λ值在0.01附近时，绝大多数变量的回归系数趋于稳定，故认为λ值可以选择在0.01附近。

1.2 交叉验证法确定λ值

可视化方法只能确定λ值的大概范围，为了能够定量地找到最佳的λ值，需要使用k重交叉验证的方法。该方法的操作思想可以借助下图来说明：

实现岭回归模型的k重交叉验证，可以使用sklearn子模块linear_model中的RidgeCV类。

RidgeCV(
alphas=(0.1, 1.0, 10.0),
fit_intercept=True,
normalize=False,
scoring=None, # 指定用于评估模型的度量方法
cv=None, # 指定交叉验证的重数
gcv_mode=None, #用于指定执行广义交叉验证的方法,取值有：“auto”、“svd”、“engin”
store_cv_values=False # bool类型参数，是否在每一个Lambda值下都保存交叉验证得到的评估信息，默认为False，只有当参数cv为None时有效。
)

使用十折交叉验证。

# 导入第三方模块
from sklearn.linear_model import RidgeCV
ridge_cv = RidgeCV(alphas=lambds,normalize=True,scoring='neg_mean_squared_error',cv=10)
# 模型拟合
ridge_cv.fit(X_train,y_train)
# 返回最佳的lambda值
ridge_best_lambda = ridge_cv.alpha_
print('最佳的lambda值为：',ridge_best_lambda)

最佳的lambda值为： 0.0013987131026472386
与可视化方法确定的λ值在0.01附近保持一致。该值的评判标准是：对于每一个λ值计算平均均方误差（MSE），然后从中挑选出最小的平均均方误差，并将对应的λ值挑选出来，作为最佳的惩罚项系数λ的值。

2 模型预测

建模的目的就是对未知数据的预测。使用交叉验证得到的最佳λ值构建岭回归模并进行预测。

# 基于最佳的lambda值建模
ridge = Ridge(alpha=ridge_best_lambda,normalize=True)
ridge.fit(X_train,y_train)
# 返回岭回归模型系数
ridge_coef = pd.Series(data=[ridge.intercept_]+ridge.coef_.tolist(),index =['Intercept']+X_train.columns.to_list())
print('岭回归模型系数:\n',ridge_coef)

# 模型预测
from sklearn.metrics import mean_squared_error # 均方误差MSE，评估模型效果
y_pred = ridge.predict(X_test)
# 预测效果验证  :均方根误差RMSE
rmse = np.sqrt(mean_squared_error(y_test,y_pred))
print("测试集均方根误差RMSE：",rmse)

岭回归模型系数:

变量名	变量值
Intercept	-334.048369
BMI	5.783170
BP	0.878213
S1	-0.859325
S2	0.480118
S3	0.450037
S4	7.609293
S5	58.340168
S6	0.365901

测试集均方根误差RMSE： 53.64384657387297

二、LASSO模型

岭回归不管怎么缩减，都会始终保留建模时的所有变量，无法降低模型的复杂度，为了克服这个缺点，运用而生LASSO回归。与岭回归模型类似，LASSO回归同样属于缩减性估计，而且在回归系数的缩减过程中，可以将一些不重要的回归系数直接缩减为0，即达到变量筛选的功能。LASSO回归为在岭回归模型中的惩罚项由平方和改成了绝对值，即惩罚项为L1正则式。

目标函数加上L1正则项的示意图

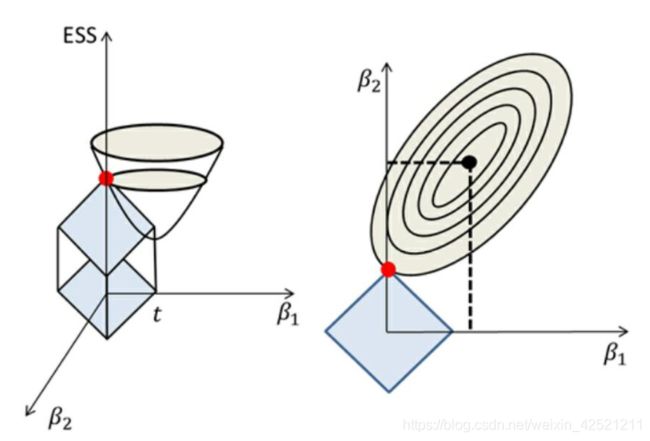
相比于圆面，L1正则项的方框顶点更容易与抛物面相交，从而起到变量筛选的效果。对于无法影响因变量的自变量，LASSO回归都将其过滤掉。

1 λ 值的确定

1.1 可视化方法确定 λ 值

在Python中，可以使用sklearn子模块linear_model中的Lasso类实现模型系数的求解。

Lasso(
alpha=1.0,
fit_intercept=True,
normalize=False,
precompute=False, # bool类型参数，是否在建模前通过计算Gram矩阵提升运算速度，默认为False
copy_X=True,
max_iter=1000,
tol=0.0001,
warm_start=False, # bool类型参数，是否将前一次的训练结果用作后一次的训练，默认为False
positive=False, # bool类型参数，是否将回归系数强制为正数，默认为False
random_state=None,
selection=‘cyclic’ # 指定每次迭代时所选择的回归系数，如果为’random’，表示每次迭代中将随机更新回归系数；如果为’cyclic’，则表示每次迭代时回归系数的更新都基于上一次运算
)

# 导入模块中的函数
from sklearn.linear_model import Lasso

# 空列表，用于存储模型的偏回归系数
lasso_coffs = []
for lambd in lambds:
    lasso = Lasso(alpha=lambd,normalize=True)
    lasso.fit(X_train,y_train)
    lasso_coffs.append(lasso.coef_)
# 绘制lambda与回归系数的折线图
plt.plot(lambds,lasso_coffs)
# 对x轴取对数
plt.xscale('log')
plt.xlabel('$\lambda$')
plt.ylabel('cofficients')
plt.show()

与岭回归模型绘制的折线图类似，出现了喇叭形折线，说明该变量存在多重共线性。当λ值落在0.05附近时，绝大多数变量的回归系数趋于稳定，所以，基本可以锁定合理的λ值范围，接下来需要通过定量的交叉验证方法获得准确的λ值。

1.2 交叉验证法确定λ值

Python的sklearn模块提供了现成的接口，只需调用子模块linear_model中的LassoCV类。

LassoCV(
eps=0.001, # 指定正则化路径长度，默认为0.001，指代Lambda的最小值与最大值之商
n_alphas=100, # 指定正则项系数Lambda的个数，默认为100个
alphas=None, # 指定具体的Lambda值列表用于模型的运算
fit_intercept=True,
normalize=False,
precompute=‘auto’,
max_iter=1000,
tol=0.0001,
copy_X=True,
cv=‘warn’, # 指定交叉验证的重数
verbose=False, # bool类型参数，是否返回模型运行的详细信息，默认为False
n_jobs=None, # 指定交叉验证过程中使用的CPU数量，即是否需要并行处理，默认为1表示不并行运行，如果为-1，表示将所有的CPU用于交叉验证的运算
positive=False,
random_state=None,
selection=‘cyclic’,
)

# 导入第三方模块
from sklearn.linear_model import LassoCV
# 交叉验证
lasso_cv = LassoCV(alphas=lambds,normalize=True,cv=10)
lasso_cv.fit(X_train,y_train)
# 输出最佳的lambda值
lasso_best_alpha = lasso_cv.alpha_
print("最佳lambda值：",lasso_best_alpha)

2 模型预测

使用交叉验证得到的最佳λ值构建LASSO回归模并进行预测。

# 基于最佳的lambda值建模
lasso = Lasso(alpha=lasso_best_alpha,normalize=True)
lasso.fit(X_train,y_train)
# 返回LASSO回归模型系数
lasso_coef = pd.Series(data=[lasso.intercept_]+lasso.coef_.tolist(),index =['Intercept']+X_train.columns.to_list())
print('lasso回归模型系数:\n',lasso_coef)

# 模型预测
from sklearn.metrics import mean_squared_error # 均方误差MSE，评估模型效果
y_pred = lasso.predict(X_test)
# 预测效果验证  :均方根误差RMSE
rmse = np.sqrt(mean_squared_error(y_test,y_pred))
print("测试集均方根误差RMSE：",rmse)

lasso回归模型系数:

Intercept	-346.957063
BMI	5.780151
BP	0.880328
S1	-0.985588
S2	0.593059
S3	0.600946
S4	8.039360
S5	61.497785
S6	0.362785

测试集均方根误差RMSE： 53.628899177363714

三、Logistic回归分类模型

1 模型特点

• 属于非线性模型，专门用来解决二分类的离散问题。又和线性回归模型有关，属于广义的线性回归分析模型；
• 该模型的一个最大特色，具有很强的解释性。

2 模型用途

可以借助该模型实现两大用途：

• 一个是寻找“危险”因素，例如，医学界通常使用模型中的优势比寻找影响某种疾病的“坏”因素；
• 另一个用途是判别新样本所属的类别，例如根据手机设备的记录数据判断用户是处于行走状态还是跑步状态。

3 模型参数的解释

• 发生比的作用只能解释为在同一组中事件发生与不发生的倍数。
• 使用发生比之比就可以解释模型参数的含义了。

4 模型的构建

可以借助于sklearn的子模块linear_model，调用LogisticRegression类。

LogisticRegression(
penalty=‘l2’,
dual=False, # bool类型参数，是否求解对偶形式，默认为False，只有当penalty参数为’l2’、solver参数为’liblinear’时，才可使用对偶形式
tol=0.0001,
C=1.0, #值越小，正则化项越大
fit_intercept=True,
intercept_scaling=1, # 当solver参数为’liblinear’时该参数有效，主要是为了降低X矩阵中人为设定的常数列1的影响
class_weight=None, # 用于指定因变量类别的权重，如果为字典，则通过字典的形式{class_label:weight}传递每个类别的权重；如果为字符串’balanced’，则每个分类的权重与实际样本中的比例成反比，当各分类存在严重不平衡时，设置为’balanced’会比较好；如果为None，则表示每个分类的权重相等
random_state=None,
solver=‘warn’,
max_iter=100,
multi_class=‘warn’,
verbose=0,
warm_start=False,
n_jobs=None,
l1_ratio=None,
)

---

1. 从零开始学Python数据分析与挖掘／刘顺祥著．—北京：清华大学出版社，2018ISBN 978-7-302-50987-5 ↩︎