6. 图像复原（上）

6.1 图像退化与复原

图像退化与复原的数学模型：

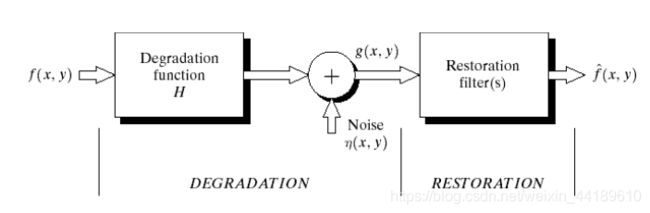
其中f(x,y)为原图像，经过H系统的退化并加上n(x,y)噪声后变成g(x,y)，这个g(x,y)就是我们可以拿到的图像，一般情况下H被看成线性移不变系统，而噪声n的形式可分为周期性的噪声和独立同分布的随机噪声。我们图像复原的目的就是从已知的g(x,y)中恢复处f(x,y)，但在实际中，我们并不知道f(x,y)，所以一般研究过程中，都是用已知的f(x,y)经过一个H并添加噪声来得到g，通过对g的恢复来得到f并和原图对比来比较复原效果好坏。
这里的噪声有很多种，下面我们就来讨论一下噪声的模型。

6.2 噪声模型

6.2.1 用imnoise添加噪声

IPT工具箱采用函数imnoise来使用噪声污染一幅图像，该函数的基本语法为：

g = imnoise(f, type, parameters);

其中，f是输入的图像，type和parameters是噪声类型和相应的参数。函数imnoice在给图像添加噪声之前，要将它转化为[0,1]内的double类图像。所以指定噪声参数时必须要考虑到，例如，要将均值为64，方差为400的高斯噪声添加到一幅uint8的图像上，我们可以将均值设为64/255，方差设为400/255^2，以便作为函数参数。该函数的语法形式如下：

G=imnoise(f,’gaussian’,m,var)
G=imnoise(f,’localvar’,V)
G=imnoise(f,’localvar’,image intensity,var)
G=imnoise(f,’salt&pepper’,d))
G=imnoise(f,’speckle’, var)
G=imnoise(f, ’poisson’)

6.2.2 产生具有指定分布的随机噪声

1）一个著名的结果: 如果w 是区间(0,1)上的一个均匀分布的随机变量，那么我们可以通过求解方程得到一个具有指定累积分布函数F(z)(CDF) 的随机变量z:

一个例子: 用瑞利CDF生成随机数z:

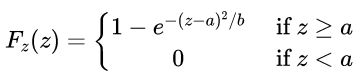
我们可以通过求解以下等式来获得:

得到：

2）随机变量表：

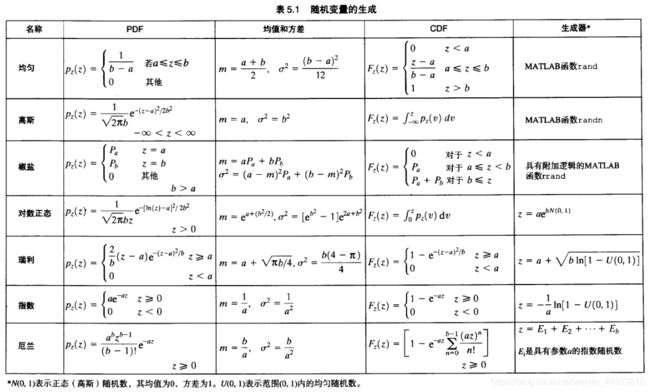
3）一些重要的概率密度函数的形状：

4）使用imnoise2生成具有指定分布的随机噪声
（1）从上面的表中可以看出每种分布都有两个参数，imnoice2函数的形式如下：

r = imnoice2(type, M, N ,a,b);

其中，type表示随机噪声服从的分布类型，M、N表示生成的随机数的行和列，a、b表示分布的参数。
（2）示例：

rg = imnoise2('gaussian',100000,1,0,1);
rr=imnoise2('rayleigh',100000,1,0,1);
ru=imnoise2('uniform',100000,1,0,1);
rl=imnoise2('lognormal',100000,1);
rex =imnoise2('exponential',100000,1);
rer =imnoise2('erlang',100000,1);


subplot(3,2,1);hist(rg,50);title('高斯分布');
subplot(3,2,2);hist(rr,50);title('瑞丽分布');
subplot(3,2,3);hist(ru,50);title('均匀分布');
subplot(3,2,4);hist(rl,50);title('对数正态');
subplot(3,2,5);hist(rex,50);title('指数分布');
subplot(3,2,6);hist(rer,50);title('厄兰分布');

6.2.3 使用imnoise3产生周期性噪声信号（在频率域滤波）

1）周期性噪声的模型为：

2）它的对应傅立叶变换：

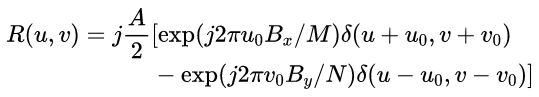
可以看出周期性信号对应的傅里叶变换是两个关于中心对称的脉冲，在傅里叶频谱中也就是两个小亮点，下面进行演示。
3）imnoise3的函数形式如下：

[r,R,S]=imnoise3(M,N,C);

其中M、N表示噪声大小，C表示在频域中的小亮点的坐标，r表示空域噪声模型，R表示傅里叶变换，S为正弦噪声模型的傅里叶的频谱。
4）示例：

C=[0 64;0 128;32 32;64 0;128 0;-32 32];
[r,R,S]=imnoise3(512,512,C);
%这里的S = abs（R）
subplot(1,2,1);imshow(S,[]);
subplot(1,2,2),imshow(r,[]);

6.2.4 噪声污染的例子

1）图像被独立噪声污染：


2）图像被周期性噪声污染：

6.2.5 估计噪声参数

1）通常通过对图像的傅里叶谱的审视来估计周期性噪声的的参数，例如通过肉眼去发现频谱中的频率尖峰。
2）尝试直接从图像推断噪声分量的周期性通常仅在简单的情况下是可行的。
3）在噪声尖峰非常明显，或者具有对干扰的频率分量一般位置的先验知识的情况下，才可以进行自动分析。
4）噪声PDF的参数可以部分从传感器规范中得知，但通常需要针对特定的成像环境估计它们，例如，一组“平坦”环境。
5）当仅有生成的图像可用时，通常可以从相对恒定灰度级的图像小区域中估计噪声PDF的参数。
6）最简单的方法就是利用图像中的采样数据来估计噪声的均值和方差。通过直方图的形状来辨识最接近PDF匹配。如果形状近似为高斯分布，均值和方差就是我们需要的全部了。对于
其他形状，我们可使用均值和方差来求解参数 a和 b。

7）统计矩与中心矩

其中0阶矩恒为1，为总概率，1阶矩恒为0，二阶矩为方差。通过计算均值和方差就可以算出相应的参数。
8）使用statmoments函数估计均值和矩

[v,unv]=statmoments(p,n)；

其中p为图像直方图向量，n为几阶矩，v为归一化矩的值，unv原始区间的矩
9）有时候我们需要通过图像特定范围来估计噪声，这就需要感兴趣区域，函数如下：

B=roipoly(f,c,r)

f是感兴趣图像，c和r是多边形顶点坐标对应的行坐标和列坐标，输出B是一个二值图像，感兴趣区域里的值为1，其余为0.为了交互性的使用感兴趣区域可以使用：

[B,c,r]=roipoly(f); % 鼠标选择

使用鼠标选择点。
示例：

f = imread('Fig0507(a)(ckt-board-orig).tif');
subplot(1,3,1);imshow(f);
[B c r] = roipoly(f);
subplot(1,3,2);imshow(B);

[p,npix] = histroi(f,c,r);
subplot(1,3,3);bar(p,1);

6.3 仅有噪音情况下的图像复原–空域滤波

如果只有噪音，图像退化模型可表示为：

6.3.1 空域噪声滤波器

1）算术平均滤波：

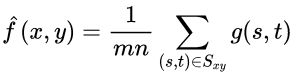
2）几何均值滤波器：

3）调和均值滤波器： 调和均值滤波器能很好地去除盐噪声，但不能滤除椒噪声。

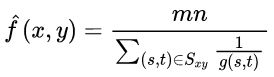
4）反调和均值滤波器：

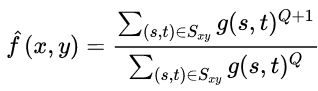
反调和均值滤波器非常适合消除盐和胡椒噪声的影响。当 Q > 0 时，该滤波器可消除椒噪声；当 Q < 0 时，它适合消除盐噪声。它不能同时消除椒盐噪声。
5）算术与几何均值滤波器的滤波效果

6）调和均值与反调和均值滤波器的滤波示例

7）中值滤波器：

8）中点滤波器：

9）最大、最小滤波器：

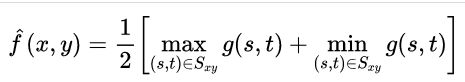
10）阿尔法均值滤波：

11）中值滤波器对椒盐噪声的滤波效果：
对椒盐噪声效果较好。

12）最大、最小值滤波器对椒盐噪声的滤波效果：

6.3.2 自适应空域中值滤波器

1）符号:

Z min = minimum intensity value in S xy
Z max = maximum intensity value in S xy
Z med = median intensity value in S xy
Z xy = intensity value at coor dinates x,y

2）自适应中值滤波算法

Level A:
If Z min < Z med < Z max , go to level B
else increase the window size
if window size ≤S max , repeat levelA
else output Z med
Level B:
If Z min < Z xy < Z max , output Z xy
else output Z med

3）自适应空域中值滤波器的滤波效果：

6.4 用频域滤波消除周期噪声

1）带阻滤波器:

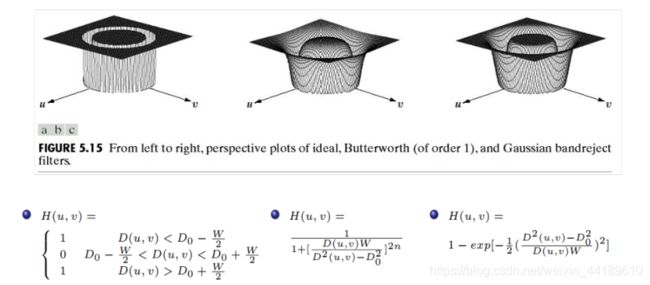
2）带阻滤波器的应用

3）带通阻滤波器:

4）陷波滤波器：

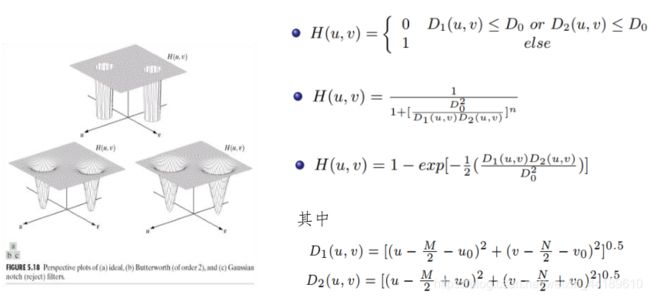
5）用陷波滤波器去除周期性噪声：

6）最佳陷波滤波算法：
（1）当存在多个干扰分量时，由于滤波过程中去除的图像信息过多，上述方法的滤波效果并不总是可以接受的。
（2）这里讨论的方法的最优是在最小化被复原图像局部方差意义下的。
（3）首先，通过如下计算获得对噪声的初始估计

其中FN(u,v)是获取噪声干扰模式的陷波滤波器。
（4）令：

我们将寻找确定调制函数w(x,y) , 来最小化f(x,y)的局部方差

目标函数：

进一步可得：

若令：

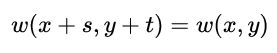
我们有：

为了最小化目标函数 , 我们要求解方程：

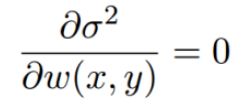
求得的结果为：

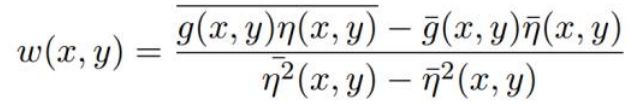
7）最佳陷波滤波算法的计算效果