【复习19-23天】【我们一起60天准备考研算法面试(大全)-第二十五天 25/60】
专注 效率 记忆
预习 笔记 复习 做题
欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录)
文章字体风格:
红色文字表示:重难点★✔
蓝色文字表示:思路以及想法★✔
如果大家觉得有帮助的话,感谢大家帮忙
点赞!收藏!转发!
本博客带大家一起学习,我们不图快,只求稳扎稳打。
由于我高三是在家自学的,经验教训告诉我,学习一定要长期积累,并且复习,所以我推出此系列。
只求每天坚持40分钟,一周学5天,复习2天
也就是一周学10道题
60天后我们就可以学完81道题,相信60天后,我们一定可以有扎实的代码基础!我们每天就40分钟,和我一起坚持下去吧!
qq群:878080619
第二十五天【考研408-数据结构(笔试)】
- 十八、BFS
-
- 1. 玛雅人的密码
- 2. 等差数列
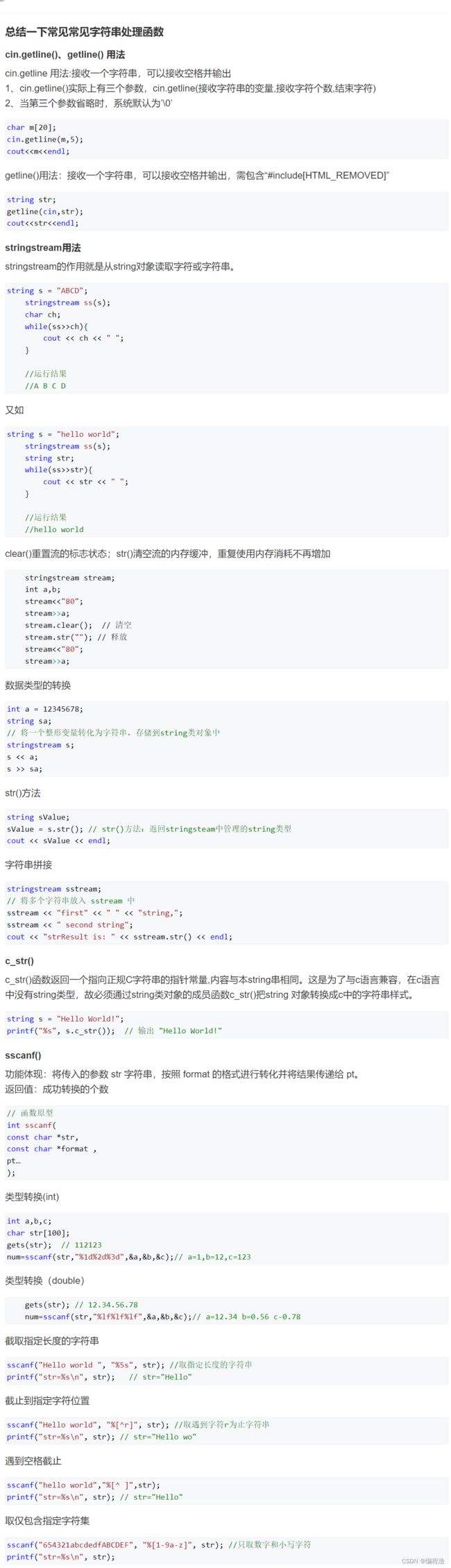
- 十九、字符串处理
-
- 1. 首字母大写
- 2. 日志排序
- 3. 字符串转换整数
- 二十、递归,画图
-
- 1. 重复者
- 二十一、背包问题
-
- 1. 01背包
- 2. 神奇的口袋( 体积恰好是 )
- 3. 整数拆分
- 二十二、高精度
-
- 1. N的阶乘
-
- 做法:预处理
- 2. 基本算术
- 3. 整数查询
十八、BFS
1. 玛雅人的密码
- 前者表示经过多次交换后当下的字符串的组成
- 后者表示达到当下的字符串状态,经过的交换次数
因为数字本身可能会重复出现,而且对于一个字符串交换它两个不同相邻位置得到的新字符串,也可能产生重复,但我们要求的是最少交换次数,因为BFS的性质,保证了可以实现最小,所以可以设置一个map映射组,来存储已经出现过的字符串情况,防止重复对相同组成的字符串再入队处理,以作到剪枝的作用,降低时间复杂度。
这道题进入BFS暴搜前,要做一些基本的判断,很容易就考虑不到,要做好了。
#include 2. 等差数列
根据样例分析出
只要每行有两个元素
那么该行就能推出所有等差数据
同理列也是
所以我们先遍历所有行和列
看哪些有两个元素的
然后根据这样行和列进行填充
填充过程中观察是否新数据使得对应的行或者列
变得大于两个元素,进而可以填充
那么该过程就想到了bfs
bfs队列存储的元素是什么呢?就是所在的行或者列
怎么判断是行还是列呢?
行的范围为(0-n)
列的范围(n,m+n)
#include 十九、字符串处理
1. 首字母大写
#include 2. 日志排序
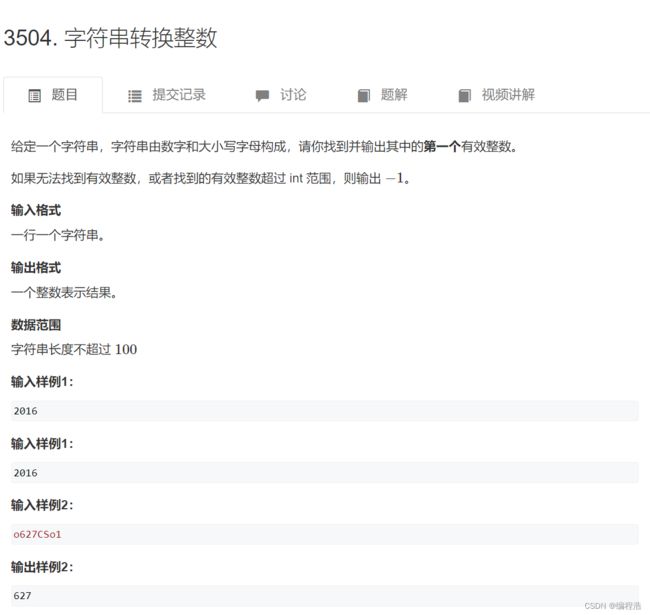
#include 3. 字符串转换整数
#include 二十、递归,画图
1. 重复者
所以需要递归
#include 二十一、背包问题
1. 01背包
#include 2. 神奇的口袋( 体积恰好是 )
#include3. 整数拆分
#include#include 二十二、高精度
1. N的阶乘
![]()
做法:预处理
#include 2. 基本算术
![]()
#include 3. 整数查询
![]()
#include