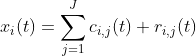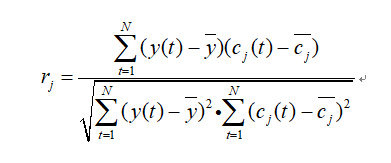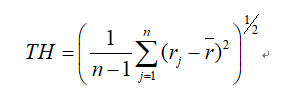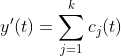EEMD算法原理及应用

目录

1.简介

2.原理

3.应用于信号去噪

3.1仿真信号

3.2信号的分解

3.3相关系数

 3.4信号的重构

4.总结

5.参考文献

---

1.简介

经验模态分解(Empirical Mode Decomposition,EMD)方法适合分析和处理非平稳、非线性信号, 但是该方法存在问题和不足之处，主要是：①用EMD分解得到的(本征模态函数)存在模态混叠现象；②末端效应影响分解效果。为了抑制EMD的模态混叠现象，法国的Handrin等人用EMD对白噪声分解后的结果进行统计，提出了基于噪声辅助分析的改进EMD方法，即集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)。

2.原理

EEMD方法的本质是一种叠加高斯白噪声的多次经验模式分解，利用了高斯白噪声具有频率均匀分布的统计特性，通过每次加入同等幅值的不同白噪声来改变信号的极值点特性，之后对多次EMD得到的相应IMF进行总体平均来抵消加入的白噪声，从而有效抑制模态混叠的产生。EEMD分解步骤如下：

（1）设定总体平均次数；

（2）将一个具有标准正态分布的白噪声加到原始信号上，以产生一个新的信号：

                               ，式中表示第  次加性白噪声序列，表示第  次试验的附加噪声信号，；

（3）对所得含噪声的信号分别进行EMD分解，得到各自和的形式：

                               

式中，为第  次加入白噪声后分解得到的第  个，是残余函数，代表信号的平均趋势，是的数量；

（4）重复步骤(2)和步骤(3)进行次，每次分解加入幅值不同的白噪声信号得到的集合为：

                                ，。

（5）利用不相关序列的统计平均值为零的原理， 将上述对应的进行集合平均运算，得到EEMD分解后最终的，即：

                               

式中，是EEMD分解的第  个，，；

3.应用于信号去噪

3.1仿真信号

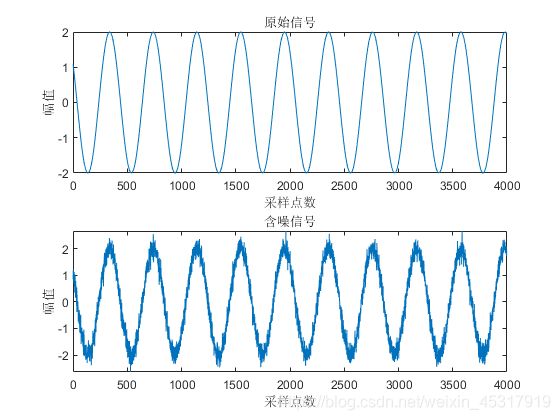
对原始信号，加入高斯白噪声，得到含噪信号，原始信号和含噪信号如图1所示。

3.2信号的分解

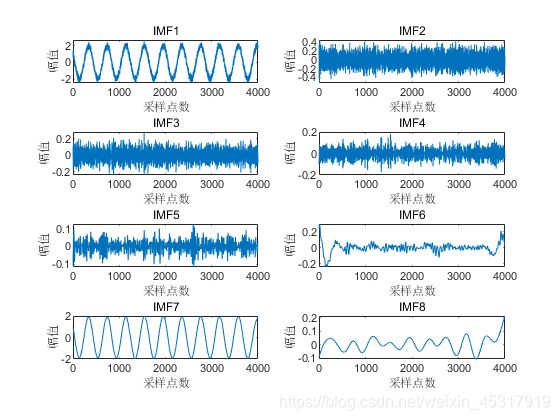
用EEMD算法对含噪信号进行分解，得到各个如图2所示。其中，IMF1是原始输入信号y，IMF2-IMF7是从高频到低频的IMF分量，IMF8是残余分量。

3.3相关系数

常用的相关系数法是将本征模式分量与原信号之间的相关系数作为一个指标，来判断哪些本征模式分量是信号的真实分量，哪些是虚假的、无意义的本征模式分量，将这些虚假本征模式分量剔除，作为残差的一部分。为了避免幅值较小而又是真实的被去除，将所有的本征模式分量与原信号进行归一化处理。本征模式分量和原信号之间的归一化相关系数为：

式中，为第  个与原信号的相关系数，为信号的采样点。

设定一阈值，由相关系数的标准差得到，即：

若，保留第  个，否则剔除第  个。

 3.4信号的重构

利用相关系数和阈值筛选出有效的  个，并对其进行叠加，即可得到去噪后的信号：

                                         

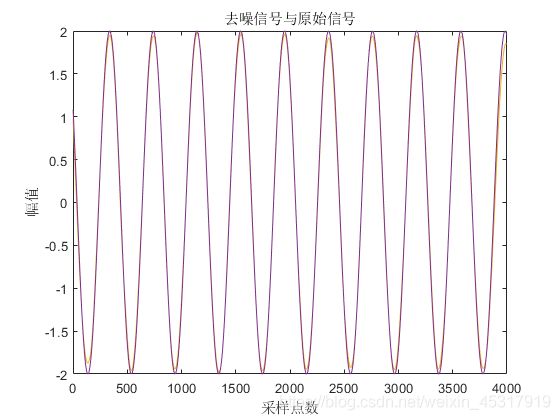
为了突出去噪效果，将去噪后的信号与原始信号放在同一坐标下，如图3所示，去噪后的信号与原始信号基本重合。

4.总结

EEMD算法是一种对非线性非平稳信号分析和处理的有效方法，解决了信号在分解过程出现的模态混叠问题，但也存在一些缺点：①分解过程中会存在残余的白噪声；②选取有效的完全依靠经验来确定。这些都影响了EEMD对信号分解重构的准确性。

本博文配套的源代码和EEMD工具见链接：EEMD算法应用于信号去噪

5.参考文献

[1]EEMD详解

[2]Wu Zhao-hua and Huang Norden E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009,1(1):1-41.

[3]王玉静,康守强,张 云,等.基于集合经验模态分解敏感固有模态函数选择算法的滚动轴承状态识别方法[J].电子与信息学报,2014,36(3):595-600.