Gumbel Softmax Trick

算法学习之gumbel softmax
【Learning Notes】Gumbel 分布及应用浅析
gumbel-softmax(替代argmax)
**重参数化技巧（Gumbel-Softmax）

重参数化技巧（re-parameters trick）

从高斯分布$N(\mu ,{\sigma }^2)$从采样$x$，改为 从标准分布$N(0,1)$中采样$z$, 再得到$x=z\ast \sigma +\mu$。这样做的好处是 将随机性转移到了$z$这个常量上，而$\sigma$和$\mu$则当作仿射变换网络的一部分（可学习参数）。

直接采样导致梯度不可导。

---

在VAE中，期望encoder学习分布$N(\mu ,{\sigma }^2)$，在从中采样一个$z$，给decoder解码。但这个采样操作是不可导的，所以使用到了重参数化技巧。

让encoder学习均值$\mu$和标准差$\sigma$，我们只需要从标准分布$N(0,1)$中采样噪声$q$，再得到$[z=q\ast \sigma +\mu ]\in N(\mu ,{\sigma }^2)$即可。

Gumbel softmax trick

解决随机采样不可导问题。

【Learning Notes】Gumbel 分布及应用浅析

例如，

对于，$\text{logits}=(x_1,x_2,...,x_k)$，我们需要（按概率）采样得到其中的一个下标，如1, 2, …。

基于Softmax的采样

利用softmax归一化$\text{logits}$，

$${\pi }_i=\frac{e^{x_i}}{{\sum }_{j=1}^k{e}^{x_j}}$$

这样得到的${\sum }_{i=1}^k{x}_i=1$。然后得到的每个${\pi }_i\in (0,1)$可以看作概率，然后使用这个概率去抽样下标。

numpy实现的soft-max方法

x = torch.randn(10)
size = 100000
def sample_with_softmax(logits, size):
    # size:     抽取次数
    # 默认有放回采样
    prob = F.softmax(logits)
    indices = torch.multinomial(prob, size, replacement=True)
    return indices

indices_softmax = sample_with_softmax(x, size)

print(x)
print(indices_softmax)

基于Gumbel-max的采样

x = torch.randn(10)
size = 100000
def sample_with_gumbel_max(logits, size):
    gumbel_dist = torch.distributions.gumbel.Gumbel(0, 1)
    noise = gumbel_dist.sample((size, logits.shape[-1]))
    indices = np.argmax(logits + noise, axis=-1)
    return indices

indices_gumbel_max = sample_with_gumbel_max(x, size)

print(indices_gumbel_max)

---

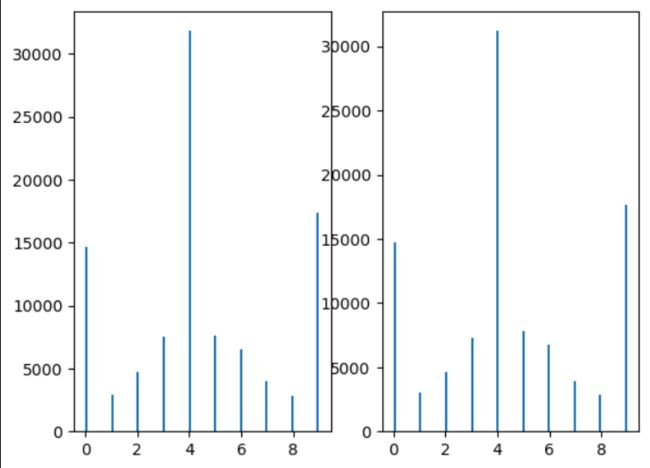
可以证明，Gumbel-max方法的采样效果等价于softmax采样的方法。

如果我们分别利用 两种方法，进行多次采样，得到如下图。

import matplotlib.pylab as plt
import numpy as np
import torch
from torch.nn import functional as F


x = torch.randn(10)
size = 100000
def softmax(x):
    x -= np.max(x)
    return np.exp(x) / np.sum(np.exp(x))

def sample_with_softmax(logits, size):
    # size:     抽取次数
    # 默认有放回采样
    prob = F.softmax(logits)
    indices = torch.multinomial(prob, size, replacement=True)
    return indices

indices_softmax = sample_with_softmax(x, size)

print(x)
print(indices_softmax)

def sample_with_gumbel_max(logits, size):
    gumbel_dist = torch.distributions.gumbel.Gumbel(0, 1)
    noise = gumbel_dist.sample((size, logits.shape[-1]))
    indices = np.argmax(logits + noise, axis=-1)
    return indices

indices_gumbel_max = sample_with_gumbel_max(x, size)

print(indices_gumbel_max)

fig, axes = plt.subplots(1, 2)
axes[0].hist(indices_softmax, bins=100)
axes[1].hist(indices_gumbel_max, bins=100)

横坐标是下标，纵坐标是下标出现的次数。对随机生成的10大小的logits，采样10万次。

这里，解决了随机采样的问题。（利用argmax我们也可以进行随机采样）

---

但如上两种采样方式，都会导致不可导的问题。

• sample_with_softmax中的np.random.choice
• sample_with_gumbel_max中的np.argmax

那有没有什么方法使它可导呢？

基于Gumbel-softmax采样

def sample_with_softmax_hard(logits, size, tau=1):
    y = F.softmax(logits / tau)
    y_hard = torch.eye(y.shape[-1])[torch.argmax(y, dim=-1)]        # ont-hot
    y_hard = y + (y_hard - y).detach()            # straight-through estimator   直接复制梯度
    return y_hard

直接将梯度复制，回传跨过argmax。称为gradient straight-through。

• 这里的tau是一个温度系数，这里暂不提及，见下文。
• 在前向过程中，我们得到的是y_hard，反向过程中计算的梯度是y。

但在sample_with_softmax_hard中，无法实现随机采样。这里我们结合上面的gumbel-max的方法。

def sample_with_gumbel_softmax(logits, size, tau=1):
    gumbel_dist = torch.distributions.gumbel.Gumbel(0, 1)
    noise = gumbel_dist.sample((size, logits.shape[-1]))
    y = F.softmax((logits+noise) / tau)
    y_hard = torch.eye(y.shape[-1])[torch.argmax(y, dim=-1)]        # ont-hot
    y_hard = y + (y_hard - y).detach()            # straight-through estimator   直接复制梯度
    return y_hard

即，给logits加上一个gumbel噪声，使得argmax能够实现随机抽样。

这里，解决了梯度的不可导。

---

Softmax中的温度系数tau

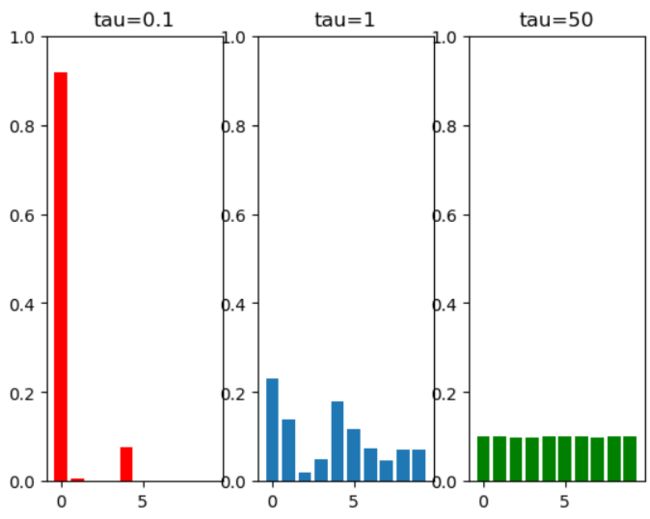
temperature 是大于零的参数，它控制着softmax的 soft 程度。温度越高，生成的分布越平滑；温度越低，生成的分布越接近离散的 one-hot 分布。 下面示例对比了不同温度下，softmax 的结果。

def softmax_plus(x, tau=1):
    y = F.softmax(x / tau)
    return y

x = torch.randn(10)
a = softmax_plus(x, tau=0.1)
b = softmax_plus(x, tau=1)
c = softmax_plus(x, tau=50)

fig, axes = plt.subplots(1, 3)
axes[0].bar(list(range(0, 10)), a, color='red')
axes[0].set_ylim(0, 1)
axes[0].set_title('tau=0.1')
axes[1].bar(list(range(0, 10)), b)
axes[1].set_ylim(0, 1)
axes[1].set_title('tau=1')
axes[2].bar(list(range(0, 10)), c, color='green')
axes[2].set_ylim(0, 1)
axes[2].set_title('tau=50')
plt.show()

横坐标是类别，纵坐标是softmax之后的值。可见，随着温度的升高，生成的概率趋于平滑。