对卷积和全连接之间关系的学习（1*1卷积与全连接层可以互换吗？）

1.对于卷积和全连接

首先我们看一张图，它是一张关于卷积的操作：

然后在看关于全连接的操作：

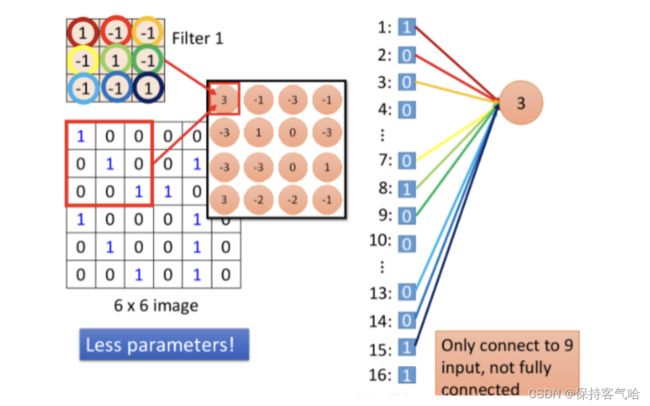
从上面两张图中可以看出卷积的过程和全连接的过程，我们利用粉色的卷积核在image上进行卷积，进行内积计算得到输出值3，如下图；那么在全连接中是如何实现的呢？

其实在全连接中相当于将6✖️6的image，也就是把6✖️6的36个pixel拉直成向量作为输入，在上图中的右边可以看到一个粉色的神经元里面的输出结果是3，它是通过一些线连接到刚才的向量上，这些线是带有权重的；当我们利用卷积核进行卷积的时候，此时卷积核考虑的9个与其重合的元素刚好对应刚才拉直的向量中编号为1，2，3，7，8，9，13，14，15的值（就是上图与彩色线相连的值），那么这些彩色线上的权重也刚好对应卷积核中的9个值，即（[[1,-1,-1],[-1,1,-1],[-1,-1,1]]），但是要注意，全连接层中的一个神经元（比如粉色3）并不是只有彩色线连接，而是还有其他线连接并且也有权重，只是除掉彩色线其他线上的权重计算结果为0，并不影响最终神经元的输出。（这里只是我看到的解释，但是我有个疑问，难道彩色线上对应的不可以是其他权重吗？只要最终的输出一样就行啊。）

所以，相比之下，全连接中的一个神经元必须连接到36个神经元，但是卷积只需要连接9个输入，这是对于检测其中一个pattern来说的，所以这样就能看出卷积的参数要少于全连接；

2.卷积中的共享参数

当我们需要另一个个pattern，也就是卷积中我们按照步距为1进行移动时，比如图中的输出结果-1，可以看出对于卷积而言，卷积核不变，所以虽然关注不同的patterm权重参数依然不变，依然共享。但是对于全连接层来说，它就会有一组不同的权重，虽然途中彩色线的权重是和卷积核中的9个一样的，但是没画出来的线中的权重是与刚才粉色3那个神经元不一样的。即每一个神经元有自己独立的权重，这样一来又可以看出卷积的参数量大大少于全连接的参数了；

3.关于1*1卷积和全连接等价的问题

图中，卷积核有3个输入通道，2个输出通道，$(K_{0,0},K_{0,1},K_{0,2})$对应输出的第一个通道的参数，$(K_{1,0},K_{1,1},K_{1,2})$对应输出的第二个通道的参数。输出由输入的浅色部分与卷积核浅色部分逐一相乘，如下：

$$I_{0,i,j}\times K_{0,0}+I_{1,i,j}\times K_{0,1}+I_{2,i,j}\times K_{0,2}$$

我们可以将$(I_{0,i,j},I_{1,i,j},I_{2,i,j})$等输入在不同通道上的向量理解成MLP网络中的特征，将$(K_{0,0},K_{0,1},K_{0,2})$等理解成MLP网络中的权重参数，特征与权重逐一相乘，这与全连接层的运算几乎一致。那么，1x1卷积层可用来完成全连接层所需要完成的工作，但是参数量上卷积要比全连接少的多。

4.关于卷积替换全连接

在3中我们知道用1*1卷积在某些情况下能够替代全连接，并能减少参数量，那如果我们的卷积核大小不是1呢？还能够替代吗？

如上图所示我们对3*3大小通道数为3的特征图进行卷积操作，采用3个3✖️3大小通道为3的卷积核大小进行卷积，得到的3个输出；

可以对应于图中的全连接操作，其中每组相同颜色的线代表一组权重，不同颜色对应的权重不一样，故根据输出可以看出有三组不同的权重，每组颜色有9个，故总共3*9=27个

对于卷积而言我们使用3个不同的卷积核，也相当于三组不同的权重，权重数量是3*9=27个

所以我们可以发现，当卷积核大小与特征图大小一样时，全连接和卷积是可以相互替换的，并且参数量是一样的。（这里是个人想法，目前还不太明白到底对不对）

5.1*1卷积的作用

1.不改变图像空间结构
全连接层会破坏图像的空间结构，例如把维度拼接成一个一维数组， 而1* 1卷积层不会破坏图像的空间结构，保留图像局部特征，卷积具有空间位置不变性。

2、输入可以是任意尺寸
全连接层的输入尺寸是固定的，因为全连接层的参数个数取决于图像大小，需要预先设定好，而卷积层的输入尺寸是任意的，因为卷积核的参数个数与图像大小无关。

3、升降维+信息交互
一张448* 448* 100 的图片在20个卷积核上做1* 1的卷积，那么结果的大小为448* 448* 20。1* 1 卷积的作用是让网络根据需要能够更灵活地控制数据的通道数（即实现不同通道之间的信息交互），通过1* 1卷积，可以将不同分支的feature map通道数调整到需要的大小，也可以升维。

4、引入非线性
卷积层之后经过激活函数，1* 1的卷积在前一层的学习表示上加了非线性激活，提升网络的非线性；

原文链接：https://blog.csdn.net/qq_44832832/article/details/128665285