红黑树删除——C语言
红黑树的删除——C语言
昨天理解了红黑树的定义、插入,旋转(左旋右旋)及相关代码实现,今天继续红黑树的删除。
可以先进行总结的是:红黑树的删除也是分两步走——第一步:像一个普通二叉查找树一样删除结点;第二步:对删除后的树进行修正。具体操作如下:
1、第一步:像一个普通二叉查找树一样删除结点并根据被删除结点的颜色决定下一步该怎么做。
//(二叉查找树删除①当待删除结点有两个孩子的时候,找到右孩子的左叶子或左孩子的右叶子,替换删除;②当待删除结点一个孩子的时候,把它的孩子接在待删除结点父结点上再删除;③叶子结点直接删除)
·当被删除结点是红色时——不需要修正,删除操作结束;
·当被删除结点是黑色时——需要进行修正(见第二步)。
2、第二步:对删除后的树进行修正。
//待修正结点为N
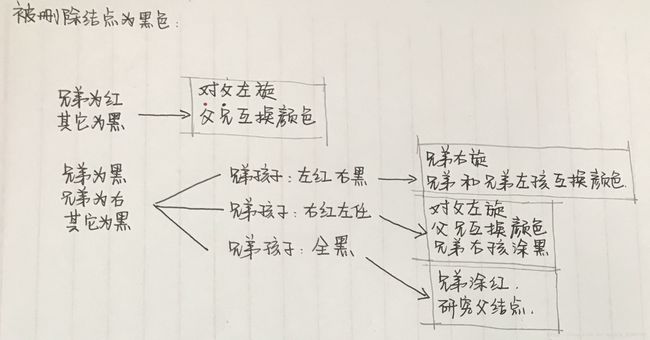
·N兄弟为红,其它都为黑时——对N父亲左旋,父兄互换颜色;
·N兄弟为黑,且N兄弟为右时——
·若N兄弟左孩子为红,右孩子为黑——N兄弟右旋,N兄弟和N兄弟左孩子互换颜色;
·若N兄弟右孩子为红,左孩子任意——N父亲左旋,N兄弟和N父亲互换颜色,兄弟右孩子涂黑;
·若N兄弟左,右孩子都为黑——N的兄弟涂红,研究父节点。
·最后待修正结点不管什么颜色都涂黑。
删除结点代码实现:
//删除
void rbtree_delete(RBRoot *root,Node *node)
{
Node *temp,*child,*parent;//替换结点
int color;
//当node有俩孩子时
if((node->lchild!=NULL)&&(node->rchild!=NULL))
{
//找到待删除结点的后继结点,即右子树的最左边的叶子结点
temp=node->rchild;
parent=node->parent;
while(temp->lchild!=NULL)
{
temp=temp->lchild;
}
//判断待删除结点是否为根节点
if(node->parent!=NULL)
{//不为根
if(node==node->parent->lchild)
{
node->parent->lchild=temp;
}
else
{
node->parent->rchild=temp;
}
}
else
{//为根
root->node=temp;
}
parent=temp->parent;//parent标记temp父结点
//child是temp的右孩子,temp必然没有左孩子,必然要对child进行调整;
child=temp->rchild;
//判断temp是否为node的父节点
if(parent==node)
{//是,直接替代
parent=temp;
}
else
{//不是,调整
//child若存在,则设为parent的左孩子
if(child!=NULL)
{
child->parent=parent;
}
parent->lchild=child;
temp->rchild=node->rchild;
node->rchild->parent=temp;
}
temp->parent=node->parent;
temp->color=node->color;
temp->lchild=node->lchild;
node->lchild->parent=temp;
}
else
{//若只有1个孩子
if(node->lchild!=NULL)
{
child=node->lchild;
}
else
{
child=node->rchild;
}
parent=node->parent;
color=node->color;
if(child!=NULL)
{
child->parent=parent;
}
if(parent!=NULL)
{//node不为根时
if(parent->lchild==node)
{
parent->lchild=child;
}
else
{
parent->rchild=child;
}
}
else
{//node为根
root->node=child;
}
}
if(color==BLACK)
{
rbtree_delete_fixup(root, child, parent);
free(node);
return;
}
} 删除修正代码实现:
//删除修正
void rbtree_delete_fixup(RBRoot *root,Node *node,Node *parent)
{
Node *bro;
int color;
while((node!=root->node)&&(node->color!=BLACK||node==NULL))//当待调结点是根结点并且是黑色的或者是空的,就跳出循环
{
if(parent->lchild==node)
{//若待调结点是左孩子
bro=parent->rchild;
if(bro->color==RED)
{//兄弟为红,其他为黑
rbtree_left_rotate(root,parent);//对父左旋
color=parent->color;//父兄交换颜色
parent->color=bro->color;
bro->color=color;
bro=parent->rchild;
}
if(bro->color==BLACK)
{// 兄弟为黑,其他为红
if(bro->lchild!=NULL&&bro->rchild!=NULL)
{
if(bro->lchild->color==RED&&bro->rchild->color==BLACK)
{//兄弟左孩子为红,右孩子为黑
rbtree_right_rotate(root,bro);//兄弟右旋
color=bro->color;//兄弟和兄弟左孩子交换颜色
bro->color=bro->lchild->color;
bro->lchild->color=color;
bro=parent->rchild;
}
if(bro->lchild->color==BLACK&&bro->rchild->color==BLACK)
{//兄弟左右孩子都为黑
bro->color=RED;//兄弟涂红
node=parent;//研究父结点
parent=node->parent;
}
if(bro->rchild->color==RED)
{// 兄弟右孩子为红,左孩子任意
rbtree_left_rotate(root,parent);//对父左旋
color=parent->color;//父兄交换颜色
parent->color=bro->color;
bro->color=color;
bro->rchild->color=BLACK;//兄弟右孩子涂黑
bro=parent->rchild;
node = root->node;
break;
}
}
}
}
else
{//若待调结点是右孩子
bro=parent->lchild;
if(bro->color==RED)
{
rbtree_left_rotate(root,parent);
color=parent->color;
parent->color=bro->color;
bro->color=color;
bro=parent->lchild;
}
if(bro->color==BLACK)
{
if(bro->lchild!=NULL&&bro->rchild!=NULL)
{
if(bro->lchild->color==RED&&bro->rchild->color==BLACK)
{
rbtree_right_rotate(root,bro);
color=bro->color;
bro->color=bro->lchild->color;
bro->lchild->color=color;
bro=parent->lchild;
}
if(bro->lchild->color==BLACK&&bro->rchild->color==BLACK)
{
bro->color=RED;
node=parent;
parent=node->parent;
}
if(bro->rchild->color==RED)
{
rbtree_left_rotate(root,parent);
color=parent->color;
parent->color=bro->color;
bro->color=color;
bro->rchild->color=BLACK;
bro=parent->lchild;
node = root->node;
break;
}
}
}
}
}
node->color=BLACK;
} 完整代码:
#include
#include
#define RED 0
#define BLACK 1
//定义红黑树结点
typedef struct RBTreeNode
{
char color;//颜色
int key;//值
struct RBTreeNode *lchild;//左孩子
struct RBTreeNode *rchild;//右孩子
struct RBTreeNode *parent;//父结点
}Node,*RBTree;
//定义红黑树根结点
typedef struct rb_root
{
Node *node;
} RBRoot;
//创建红黑树,返回红黑树的根
RBRoot* creat_rbtree()
{
RBRoot *root=(RBRoot*)malloc(sizeof(RBRoot));//定义根结点,并分配空间
root->node=NULL;//初始化
return root;
}
//新建一个结点
Node* creat_rbtree_node(int key,Node *parent,Node *lchild,Node *rchild)
{
Node* p;
p=(Node*)malloc(sizeof(Node));
p->key=key;
p->lchild=lchild;
p->rchild=rchild;
p->color=BLACK;
return p;
}
//左旋
void rbtree_left_rotate(RBRoot *root,Node *x)
{
Node *y=x->rchild;//设置x的右结点等于y
//首先,先找到y的左孩子,它最终被x收养为右孩子
x->rchild=y->lchild;
if (y->lchild!= NULL)
y->lchild->parent = x;
y->parent=x->parent;
//x->rchild=y->lchild;
//y->lchild->parent=x;
//y缺了左孩子,x成为y的左孩子
if(x->parent==NULL)//当x为根结点的时候
{
root->node=y;//将y设为根结点
}
else//当x不是根节点的时候
{
//y->parent=x->parent;//y接替x做别人的儿子
if(x->parent->lchild==x) //要确定y是做的左孩子还是右孩子
{
x->parent->lchild=y;
}
else
{
x->parent->rchild=y;
}
}
y->lchild=x;//x就位
x->parent=y;
//printf("(对关键字%d进行左旋)",x->key);
}
//右旋
void rbtree_right_rotate(RBRoot *root,Node *y)
{
Node *x=y->lchild;
y->lchild=x->rchild;
//找到x的右孩子,它最终被y收养为左孩子
if(x->rchild!=NULL)
{
x->rchild->parent=y;
}
x->parent=y->parent;
//此时x的右孩子是空的,y来当x的右孩子
if(y->parent==NULL)//如果y为根结点
{
root->node=x;//将x设为根节点
}
else//当y不是根节点的时候
{
//y->parent=x->parent;//x接替y做别人的儿子
if(y->parent->rchild==y) //要确定x是做的左孩子还是右孩子
{
y->parent->rchild=x;
}
else
{
y->parent->lchild=x;
}
}
x->rchild=y;//y就位
y->parent=x;
//printf("(对关键字%d进行右旋)",y->key);
}
//插入修正
void rbtree_insert_fixup(RBRoot *root, Node *node)
{
Node *parent, *gparent;
// 若父节点存在,并且父节点的颜色是红色
while ((parent = node->parent) && (parent->color==RED))
{
gparent = parent->parent;
//若“父节点”是“祖父节点的左孩子”
if (parent == gparent->lchild)
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->rchild;
if (uncle && uncle->color==RED)
{//父、叔变黑,爷变红,对爷进行判断
uncle->color=BLACK;
parent->color=BLACK;
gparent->color=RED;
node = gparent;
continue;
}
}
// Case 2条件:叔叔是黑色,且当前节点是右孩子
if (parent->rchild == node)
{
Node *tmp;
rbtree_left_rotate(root, parent);//父左旋
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是左孩子。
parent->color=BLACK;
gparent->color=RED;
rbtree_right_rotate(root, gparent);
}
else//若“z的父节点”是“z的祖父节点的右孩子”
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->lchild;
if (uncle && (uncle->color==RED))
{
uncle->color=BLACK;
parent->color=BLACK;
gparent->color=RED;
node = gparent;
continue;
}
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子
if (parent->lchild == node)
{
Node *tmp;
rbtree_right_rotate(root, parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子。
parent->color=BLACK;
gparent->color=RED;
rbtree_left_rotate(root, gparent);
}
}
// 将根节点设为黑色
root->node->color=BLACK;
//printf("对关键字%d进行插入修正",node->key);
}
//插入
void rbtree_insert(RBRoot *root,Node *node)
{
Node *y=NULL;
Node *x=root->node;
while(x!=NULL)//x为叶子结点跳出循环
{
y=x;
if(x->key>node->key)
{
x=x->lchild;
}
else
{
x=x->rchild;
}
}
node->parent=y;
if(y!=NULL)
{
if(node->keykey)
{
y->lchild=node;
}
else
{
y->rchild=node;
}
}
else
{
root->node=node;//若y为NULL,说明树为空,则将node设为根节点
}
node->color=RED;//将颜色设为红色
//插入修正
rbtree_insert_fixup(root, node);
}
int insert_rbtree(RBRoot *root,int key)
{
Node *node;//新建一个结点
node=creat_rbtree_node(key,NULL,NULL,NULL);
if(node==NULL) return -1;
else rbtree_insert(root,node);
return 0;
}
/*
* 中序遍历"红黑树"
*/
void inorder(RBTree tree)
{
if(tree != NULL)
{
inorder(tree->lchild);
printf("%d", tree->key);
if(tree->color==0)
{
printf("(RED) ");
}
else
{
printf("(BLACK) ");
}
inorder(tree->rchild);
}
}
void inorder_rbtree(RBRoot *root)
{
if (root)
inorder(root->node);
}
//遍历查找结点key
Node* search(RBTree x,int key)
{
if(x==NULL)
{
printf("\n**********删除失败,查无此数**********\n");
}
if(x->key==key)
{
return x;
}
if(x->keyrchild,key);
}
else
{
search(x->lchild,key);
}
}
//删除修正
void rbtree_delete_fixup(RBRoot *root,Node *node,Node *parent)
{
Node *bro;
int color;
while((node!=root->node)&&(node->color!=BLACK||node==NULL))//当待调结点是根结点并且是黑色的或者是空的,就跳出循环
{
if(parent->lchild==node)
{//若待调结点是左孩子
bro=parent->rchild;
if(bro->color==RED)
{//兄弟为红,其他为黑
rbtree_left_rotate(root,parent);//对父左旋
color=parent->color;//父兄交换颜色
parent->color=bro->color;
bro->color=color;
bro=parent->rchild;
}
if(bro->color==BLACK)
{// 兄弟为黑,其他为红
if(bro->lchild!=NULL&&bro->rchild!=NULL)
{
if(bro->lchild->color==RED&&bro->rchild->color==BLACK)
{//兄弟左孩子为红,右孩子为黑
rbtree_right_rotate(root,bro);//兄弟右旋
color=bro->color;//兄弟和兄弟左孩子交换颜色
bro->color=bro->lchild->color;
bro->lchild->color=color;
bro=parent->rchild;
}
if(bro->lchild->color==BLACK&&bro->rchild->color==BLACK)
{//兄弟左右孩子都为黑
bro->color=RED;//兄弟涂红
node=parent;//研究父结点
parent=node->parent;
}
if(bro->rchild->color==RED)
{// 兄弟右孩子为红,左孩子任意
rbtree_left_rotate(root,parent);//对父左旋
color=parent->color;//父兄交换颜色
parent->color=bro->color;
bro->color=color;
bro->rchild->color=BLACK;//兄弟右孩子涂黑
bro=parent->rchild;
node = root->node;
break;
}
}
}
}
else
{//若待调结点是右孩子
bro=parent->lchild;
if(bro->color==RED)
{
rbtree_left_rotate(root,parent);
color=parent->color;
parent->color=bro->color;
bro->color=color;
bro=parent->lchild;
}
if(bro->color==BLACK)
{
if(bro->lchild!=NULL&&bro->rchild!=NULL)
{
if(bro->lchild->color==RED&&bro->rchild->color==BLACK)
{
rbtree_right_rotate(root,bro);
color=bro->color;
bro->color=bro->lchild->color;
bro->lchild->color=color;
bro=parent->lchild;
}
if(bro->lchild->color==BLACK&&bro->rchild->color==BLACK)
{
bro->color=RED;
node=parent;
parent=node->parent;
}
if(bro->rchild->color==RED)
{
rbtree_left_rotate(root,parent);
color=parent->color;
parent->color=bro->color;
bro->color=color;
bro->rchild->color=BLACK;
bro=parent->lchild;
node = root->node;
break;
}
}
}
}
}
node->color=BLACK;
}
//删除
void rbtree_delete(RBRoot *root,Node *node)
{
Node *temp,*child,*parent;//替换结点
int color;
//当node有俩孩子时
if((node->lchild!=NULL)&&(node->rchild!=NULL))
{
//找到待删除结点的后继结点,即右子树的最左边的叶子结点
temp=node->rchild;
parent=node->parent;
while(temp->lchild!=NULL)
{
temp=temp->lchild;
}
//判断待删除结点是否为根节点
if(node->parent!=NULL)
{//不为根
if(node==node->parent->lchild)
{
node->parent->lchild=temp;
}
else
{
node->parent->rchild=temp;
}
}
else
{//为根
root->node=temp;
}
parent=temp->parent;//parent标记temp父结点
//child是temp的右孩子,temp必然没有左孩子,必然要对child进行调整;
child=temp->rchild;
//判断temp是否为node的父节点
if(parent==node)
{//是,直接替代
parent=temp;
}
else
{//不是,调整
//child若存在,则设为parent的左孩子
if(child!=NULL)
{
child->parent=parent;
}
parent->lchild=child;
temp->rchild=node->rchild;
node->rchild->parent=temp;
}
temp->parent=node->parent;
temp->color=node->color;
temp->lchild=node->lchild;
node->lchild->parent=temp;
}
else
{//若只有1个孩子
if(node->lchild!=NULL)
{
child=node->lchild;
}
else
{
child=node->rchild;
}
parent=node->parent;
color=node->color;
if(child!=NULL)
{
child->parent=parent;
}
if(parent!=NULL)
{//node不为根时
if(parent->lchild==node)
{
parent->lchild=child;
}
else
{
parent->rchild=child;
}
}
else
{//node为根
root->node=child;
}
}
if(color==BLACK)
{
rbtree_delete_fixup(root, child, parent);
free(node);
return;
}
}
void delete_rbtree(RBRoot *root,int key)
{
Node *z,*node;
z=search(root->node,key);
if(z!=NULL)
{
rbtree_delete(root,z);
}
}
int main()
{
int a[15]={2,10,6,7,15,4,14,1,13,3,8,12,5,9,11};
int i;//计数器
int key;
int n=sizeof(a)/sizeof(int);
printf("**********原始数据**********\n");
for(i=0;i 运行结果:
总结:学会了看代码,根据自己总结的思路敲下来,但是细节还是容易出错,望自己能多看多敲。快被蚊子咬死了啊啊啊啊啊!╰(‵□′)╯
我真是个小聪明━┳━ ━┳━
思路参考
代码参考