数据结构-顺序表详解(含完整代码)
文章目录
- 1.线性表的顺序存储结构
-
- 1.1定义
- 1.2 数据长度和线性表长度的区别
- 1.3顺序存储的结构代码
- 1.4顺序表中基本操作的实现
-
- 1.4.1自定义变量
- 1.4.2 初始化
- 1.4.3 查找
- 1.4.4 插入
- 1.4.5 删除
- 1.4.6 打印
- 1.5完整代码实现(*==结合完整代码再看模块理解更快==*)
- 1.6顺序表的优缺点
-
- 1.6.1 优点
- 1.6.2 缺点

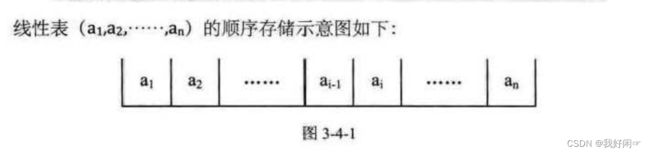
1.线性表的顺序存储结构
1.1定义
1.2 数据长度和线性表长度的区别
数据长度: 是存放线性表的存储空间的长度,存储分配后这个量一般是不变的。
线性表长度: 线性表长度是线性表数据元素的个数,会随着插入和删除操作的进行,这个量也会发生改变。
1.3顺序存储的结构代码
#define MAXSIZE 20 /*存储空间初始分配量*/
typedef int ElemType; /*ElemType的类型根据实际情况而定*/
//存储
typedef struct
{
ElemType data[MAXSIZE]; /*数组存储数据元素,最大值为MAXSIZE*/
int length; /*线性表当前长度*/
}SqList;
1.4顺序表中基本操作的实现
1.4.1自定义变量
为了方便读者对后续代码的理解,我将我自定义的一些变量放在该部分的开头
#define OK 1
#define ERROR 0
#define MAXSIZE 20 /*存储空间初始分配量*/
typedef int ElemType; /*ElemType的类型根据实际情况而定*/
typedef int Status;
1.4.2 初始化
顺序表初始化操作就是构造一个空的顺序表。
代码如下:
//初始化操作
void InitList(SqList* L)
{
int i = 0;
for (i = 0;i < MAXSIZE;i++)
{
L->data[i] = 0;
}
L->length = 0;
}
1.4.3 查找
两种不同的查找
1.顺序表按数据值查找,返回位序:
【算法步骤】
①从第一个元素起,依次将其值和e相比较,若找到与e相等的元素L.elem[i],则查找成功,返回该元素序号i+1。
②若查遍整个顺序表都没有找到,则查找失败,返回0。
【算法描述】【伪代码】
//顺序表按数据值查找,返回位序
Status LocateElem(SqList L, ElemType e)
{//在顺序表中查找值为e的数据元素,返回其序号
int i = 0;
for (i = 0;i < L.length;i++)
{
if (L.data[i] == e)
return i + 1; //查找成功
}
return 0; //查找失败
}
【算法分析】
最好的情况:查找1次
最坏的情况:查找n次
平均情况:(1+n)/2次
时间复杂度为:O(n)
2.获得元素操作,顺序表按位序查找,返回数据值
【算法步骤】
①判断指定的位置序号i值是否合理(i>=1&&i<=L.length)以及顺序表是否可查找,若不合理,返回ERROR。
②获得合理位序的数据值,返回OK。
【算法描述】【伪代码】
//获得元素操作,顺序表按位序查找,获得数据值
Status GetElem(SqList L, int i, ElemType* e)
{
if (L.length == 0 || i<1 || i>L.length)
{
return ERROR;
}
*e = L.data[i-1];
return OK;
}
【算法分析】
时间复杂度为:O(1)
1.4.4 插入
【算法步骤】
①判断插入位置i是否合法(i>=1&&i<=L.length+1),若不合法返回ERROR。
②判断顺序表的存储空间是否已满,若满则返回ERROR。
③将第n个至第i个位置的元素依次向后移动一个位置,空出第i个位置(i=n+1时无需移动)。
④将要插入的新元素e放入第i个位置。
⑤表长加1。
【算法描述】【伪代码】
//插入操作
Status ListInsert(SqList* L, int i, ElemType e)
{
int j;
if (L->length == MAXSIZE) /*顺序表已满*/
return ERROR;
if (i<1 || i>L->length+1)
return ERROR; /*当i不在范围内*/
if (i >= 1 && i <= L->length) /*写这个条件便于理解*/
{
for (j = L->length - 1;j >= i - 1;j--)
{
L->data[j + 1] = L->data[j]; /*将插入位置及之后的元素后移一位*/
}
}
L->data[i - 1] = e; /*将新元素插入*/
L->length++; /*表长加1*/
return OK;
}
【算法分析】
当在顺序表中某个位置插入一个数据元素时,其主要时间耗在数据元素移动上,而移动元素的个数(n-i)取决于插入元素的位置。
最好的情况:插入到表尾,移动0次
最坏的情况:插入到表头,移动n次
平均情况:n/2次
时间复杂度:O(n)
1.4.5 删除
【算法步骤】
①判断删除位置是否合法(i>=1&&i<=n),若不合法则返回ERROR。
②将第i+1个至第n个元素依次向前移动一个位置(i=n时无需移动)
③表长减1
【算法描述】【伪代码】
//删除操作
Status ListDelete(SqList* L, int i, ElemType* e)
{
int j;
if (L->length == 0)
return ERROR; /*线性表为空*/
if (i<1 || i>L->length)
return ERROR; /*删除位置不正确*/
*e = L->data[i - 1];
if (i >= 1 && i <= L->length)
{
for (j = i ;j < L->length;j++)
{
L->data[j - 1] = L->data[j]; /*将删除位置后继元素前移*/
}
}
L->length--; //线性表减1
return OK;
}
【算法分析】
当要删除顺序表中某个位置的元素,其主要时间耗在数据元素的移动上,而移动的个数(n-i)取决于要删除的位置。
最好的情况:删除顺序表中最后一个元素,移动0次
最坏的请况:删除顺序表中第一个元素,移动n-1次
平均情况:移动(n-1)/2
时间复杂度:O(n)
1.4.6 打印
直接【伪代码】
//打印操作
void print(SqList L)
{
int i = 0;
for (i = 0;i < L.length;i++)
printf("%d ", L.data[i]);
printf("\n");
}
1.5完整代码实现(结合完整代码再看模块理解更快)
//顺序表的整体实现
#define OK 1
#define ERROR 0
#define MAXSIZE 20 /*存储空间初始分配量*/
typedef int ElemType; /*ElemType的类型根据实际情况而定*/
typedef int Status;
//存储
typedef struct
{
ElemType data[MAXSIZE]; /*数组存储数据元素,最大值为MAXSIZE*/
int length; /*线性表当前长度*/
}SqList;
//初始化操作
void InitList(SqList* L)
{
int i = 0;
for (i = 0;i < MAXSIZE;i++)
{
L->data[i] = 0;
}
L->length = 0;
}
//顺序表按数据值查找,返回位序
Status LocateElem(SqList L, ElemType e)
{//在顺序表中查找值为e的数据元素,返回其序号
int i = 0;
for (i = 0;i < L.length;i++)
{
if (L.data[i] == e)
return i + 1; //查找成功
}
return 0; //查找失败
}
//获得元素操作,顺序表按位序查找,获得数据值
Status GetElem(SqList L, int i, ElemType* e)
{
if (L.length == 0 || i<1 || i>L.length)
{
return ERROR;
}
*e = L.data[i-1];
return OK;
}
//插入操作
Status ListInsert(SqList* L, int i, ElemType e)
{
int j;
if (L->length == MAXSIZE) /*顺序表已满*/
return ERROR;
if (i<1 || i>L->length+1)
return ERROR; /*当i不在范围内*/
if (i >= 1 && i <= L->length)
{
for (j = L->length - 1;j >= i - 1;j--) /*将要插入位置后数据元素向后移一位*/
{
L->data[j + 1] = L->data[j];
}
}
L->data[i - 1] = e; /*将新元素插入*/
L->length++; /*表长加1*/
return OK;
}
//删除操作
Status ListDelete(SqList* L, int i, ElemType* e)
{
int j;
if (L->length == 0)
return ERROR; /*线性表为空*/
if (i<1 || i>L->length)
return ERROR; /*删除位置不正确*/
*e = L->data[i - 1];
if (i >= 1 && i <= L->length)
{
for (j = i ;j < L->length;j++)
{
L->data[j - 1] = L->data[j]; /*将删除位置后继元素前移*/
}
}
L->length--; //线性表减1
return OK;
}
//打印操作
void print(SqList L)
{
int i = 0;
for (i = 0;i < L.length;i++)
printf("%d ", L.data[i]);
printf("\n");
}
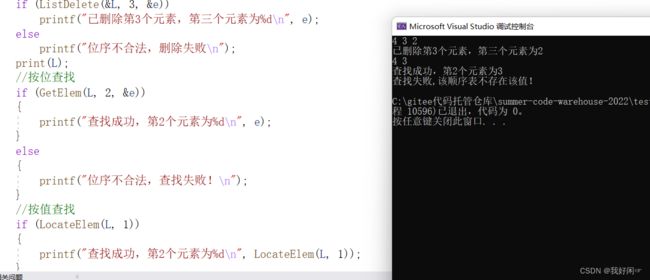
int main()
{
SqList L; //声明一些顺序表
InitList(&L);
//插入一些元素
ListInsert(&L, 1, 2);
ListInsert(&L, 1, 3);
ListInsert(&L, 1, 4);
print(L);
int e = 0; //将需要的元素带回
if (ListDelete(&L, 3, &e))
printf("已删除第3个元素,第三个元素为%d\n", e);
else
printf("位序不合法,删除失败\n");
print(L);
//按位查找
if (GetElem(L, 2, &e))
{
printf("查找成功,第2个元素为%d\n", e);
}
else
{
printf("位序不合法,查找失败!\n");
}
//按值查找
if (LocateElem(L, 1))
{
printf("查找成功,第2个元素为%d\n", LocateElem(L, 1));
}
else
{
printf("查找失败,该顺序表不存在该值!\n");
}
return 0;
}
1.6顺序表的优缺点
1.6.1 优点
顺序表可以随机存取表中任意元素,其存储位置可用一个简单、直观的公式来表示。
1.6.2 缺点
在做插入和删除操作时,需要移动大量元素。另外数组有长度相对固定的静态特性,当表中元素个数较多且变化较大时,操作过程相对复杂,必然导致存储空间的浪费。