【LeetCode刷题】动态规划实战——0-1背包问题(附Python代码)
1. 理论基础
动态规划是一种用空间换时间的方法,
如果需要重复计算某个数,就把它记下来,以避免重复运算。——by 左神
适用范围:结果仅与状态有关,与达到该状态的路径无关。
注:之所以有这个使用范围限制,是因为 dp 表仅记录状态信息,没有记录是如何达到该状态的。
解题步骤:
【1】问题拆解。看问题是否能拆解成若干子问题。
【2】定义状态。确定 dp 表的维度。
【3】确定状态转移方式。这里要做到不遗漏,找到每一条达到该状态的路径。
【4】确定初始状态。根据状态转移方式,确定所需的初始状态。
(以上,略去教科书上的概念,写写我自己的理解,如有不准确的地方请大佬们指正)
2. 0-1 背包问题
变量说明:
背包容量为 bag
物品共有 num 个
物品的重量为 weights :[w_0,w_1,…,w_num-1]
物品的价值为 values:[v_0,v_1,…,v_num-1]
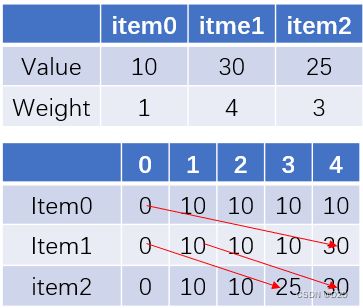
2.1 二维 dp 表
定义 dp[item][w] 为 当背包容量为 w 时,考虑前 item 项物品,背包所装物品的最大价值。
因此,dp[item] 的价值,与 dp[item-1] 的价值相关。
首先要判断 第 item 号物品是否能够装入当前背包,如果可以,则在 dp[item-1] 的基础上得到 dp[item] 的路径有两条:
- 选择装第 item 项物品
d p [ i t e m ] [ w ] = d p [ i t e m − 1 ] [ w − w e i g h t s [ i t e m ] ] + v a l u e s [ i t e m ] dp[item][w] = dp[item - 1][w - weights[item]] + values[item] dp[item][w]=dp[item−1][w−weights[item]]+values[item] - 选择不装第 item 项物品
d p [ i t e m ] [ w ] = d p [ i t e m − 1 ] [ w ] dp[item][w] = dp[item - 1][w] dp[item][w]=dp[item−1][w]
def bagTwoDe(bag, weights, values):
"""
关于第 item 号物品
不装: dp[item][w] = dp[item - 1][w]
装: dp[item][w] = dp[item - 1][w - weights[item]] + values[item]
发现可以做一些空间优化
"""
num = len(weights)
dp = [[0] * (bag + 1) for _ in range(num)]
for item in range(num):
for b in range(1, bag + 1):
if weights[item] > b:
dp[item][b] = dp[item - 1][b]
else:
dp[item][b] = max(dp[item - 1][b - weights[item]] + values[item], dp[item - 1][b])
return dp[-1][-1]
写一个测试用的例子
if __name__ == '__main__':
bag = 4
weights = [1, 4, 3]
values = [10, 30, 25]
a = bagTwoDe(bag, weights, values)
print(a)
2.2一维 dp 表
其实可以发现如果把dp[item- 1]那一层拷贝到dp[item]上,表达式完全可以是:dp[item][w] = max(dp[item][w], dp[item[w - weights[item]] + values[item]);因此,dp 表仅需要最后一行就可以了。代码如下
def bagOneDe(bag, weights, values):
"""
用一维数组存储时,背包重量应该倒序遍历,防止需要的数值被修改
"""
nums = len(weights)
dp = [0] * (bag + 1)
for item in range(nums):
for b in range( bag,-1,-1):
if weights[item] <= b:
dp[b] = max(dp[b], dp[b - weights[item]] + values[item])
return dp[-1]
if __name__ == '__main__':
bag = 4
weights = [1, 4, 3]
values = [10, 30, 25]
b = bagOneDe(bag, weights, values)
print(b)
3. Leetcode 上关于0-1背包的题目
416 分割等和子集
class Solution:
def canPartition(self, nums: List[int]) -> bool:
target = sum(nums) / 2
if int(target) != target:
return False
else:
target=int(target)
n=len(nums)
# col range(0,target)
# row range(0,n)
dp=[0]*(target+1)
for item in nums:
for w in range(target,-1,-1):
if item<=w:
dp[w]=max(dp[w],dp[w-item]+item)
if dp[-1]==target:
return True
else:
return False
1049. 最后一块石头的重量 II
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
# 0-1 bag
stonesum = sum(stones)
target = stonesum >> 1
dp = [0] * (target + 1)
for i in stones:
for j in range(target, -1, -1):
if i <= j:
dp[j] = max(dp[j], dp[j - i] + i)
return stonesum-2*dp[-1]