【0-1背包问题】——回溯法

问题描述：

        给定的n种物品和一个容量W的背包，物品i的重量为wi，价值为vi。问如何选择装入背包的物品，使得装入背包中的物品总价值最大？

问题分析：

        基本思想就是遍历这棵树，以枚举所有情况，最后进行判断，如果重量不超过背包容量，且价值最大的话，该方案就是最后的答案。        

        按照回溯法的算法框架，首先需要定义问题的解空间，然后确定解空间的组织结构,最后进行搜索。搜索前要解决两个关键问题，一是确定问题是否需要约束条件(用于判断是否有可能产生可行解),如果需要，如何设置?二是确定问题是否需要限界条件(用于判断是否有可能产生最优解)，如果需要，如何设置?

解题步骤：

        1.定义问题的解空间

        2.确定解空间的组织结构

        3.搜索解空间（设置约束条件、限界条件）

例如：

i	1	2	3	4	5
w(重量)	2	2	6	5	4
v(价值）	3	6	5	4	6

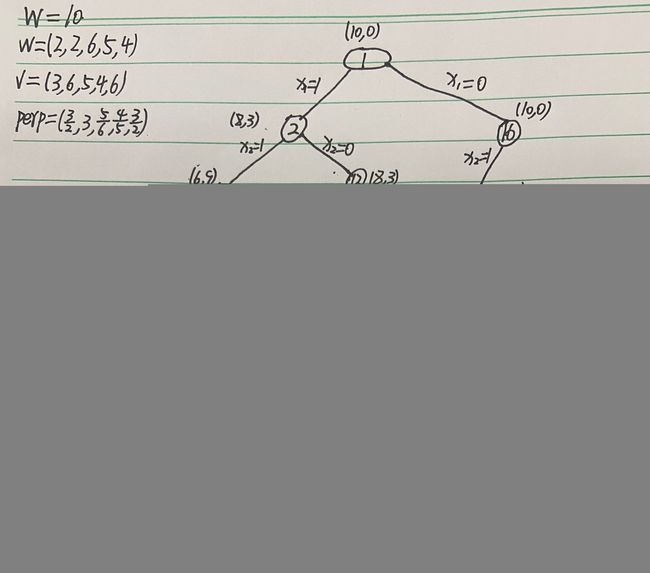
搜索过程演示（自己手画的各位凑合着看）：

问题建模：

        约束条件：wi<=W`(W`为包的剩余容量)  ∑wixi<=W.

        限界条件：cp+brp>bestp

        cp:已装入背包的前t种物品的总价值;

        brp:表示剩余容量所能容纳的从第t+1种物品到第n种物品的最大价值;

        计算方法：事先计算出物品单位重量的价值，按从大到小排序，依次装入背包，将剩余容量装满得到的价值，即为brp;

        bestp:当前已将找到的最大解的价值（初值为0）。

算法设计：

伪码：

        上界函数：Bound(i)

1.cleft<- c-cw //剩余容量
2.b<- cp
3.While i<=n and w[i]<=cleft do  // 以物品单位重量价值递减序装入物品
4.	  cleft<- cleft-w[i]
5.	  b<- b+p[i]
6.	  i<-i+1
7.end while
8.if i<=n then   //装满背包，第i件物品未装入，分割装入
9.	  b<-b+p[i]/w[i]*cleft
10.end if
11.return b

        回溯函数：Backtrack(t)

1.if t>n then  //递归结束的判定
2.	for j to n do
3.	  bestx[j]<-x[j]
4.	bestp<- cp
5.	return
6.end if
7.if cw+w[t]<=c then  //搜索左子树
8.	x[t]<-1
9.	cw<- cw+w[t]
10.	cp<- cp+v[t]
11.	Backtrack(t+1) // 深度搜索下一层  
12.	cw<- cw-w[t]   //回溯
13.	cp<- v[t]   //回溯
14.end if
15.if Bound(t+1)>bestp then  // 搜索右子树
16.    x[t]<-0
17.    Backtrack(t+1)
18.end if

算法分析：

时间复杂度分析：

        判断约束函数需0(1),在最坏情况下有2^n-1个左孩子，约束函数耗时最坏为0(2^n)。

        计算上界限界函数需要O(n)时间,在最坏情况下有2^n-1个右孩子需要计算上界,限界函数耗时最坏为O(n2^n)。

        0-1背包问题的回溯算法所需的计算时间为0(2^n)+O(n2^n)=O(n2^n)。

源码：

#include 
#include  
using namespace std;

//各个物品的重量　weight 各个物品的价值value 
double w[6]={0,2,2,6,5,4},v[6]={0,3,6,5,4,6};
double c=10; // 背包容量 
double cw=0.0; //当前背包重量　current weight
double cp=0.0; //当前背包中物品总价值　current value
double bestp=0.0;  // 当前最优价值best price 
double perp[6]; // 单位物品价值(排序后)per price 
int order[6]; //物品编号
int x[6]; //是否装入背包 
int n=5; // 物品个数 

// 排序 
void knapsack(){
    int temporder = 0;
    double temp = 0.0;
	
	for(int i=1;i<=n;i++){
		order[i]=i;
		perp[i]=v[i]/w[i]; //计算单位价值(单位重量的物品价值)
	}
    for(int i=1;i<=n-1;i++){
    	for(int j=1;j<=n-1-i;j++){
    		if(perp[j]>perp[j+1]){
    			temp = perp[j+1];  //冒泡对perp[]排序 
            	perp[j+1]=perp[j]; 
            	perp[j]=temp;
 
            	temporder=order[j+1];//冒泡对order[]排序 
            	order[j+1]=order[j];
            	order[j]=temporder;
 
            	temp = v[j+1];//冒泡对v[]排序
            	v[j+1]=v[j];
            	v[j]=temp;
 
            	temp=w[j+1];//冒泡对w[]排序
            	w[j+1]=w[j];
            	w[j]=temp;
			}
		}
	}

} 


// 计算上界函数，为了剪枝 
double Bound(int i){
	double cleft= c-cw; // 剩余背包容量
	double b=cp; // 记录当前背包的总价值cp，最后求上界
	
	// 以物品单位重量价值递减次序装入物品
	while(i<=n && w[i]<=cleft){
		cleft -= w[i];
		b+=v[i];
		i++;
	} 
	// 装满背包 
	if(i<=n)
		b+=v[i]/w[i]*cleft;
	return b; // 返回计算出的上界 
}



// 回溯函数  
void backtrack(int i){
	// 用i来指示到达的层数(第几步，从0开始)，同时也表示
	// 当前选择完了几个物品 
	
	// 递归结束的判定 
	if(i>n) {
		bestp = cp;
		return;
	}
	
	// 如若左子节点可行，则直接搜索左子树；
	// 对于右子树，先计算上界函数，以判断是否进行剪枝  
	if(cw+w[i]<=c){  // 将物品i放入背包，搜索左子树 
		x[i]=1;  
		cw +=w[i]; // 同步当前背包的重量 
		cp +=v[i]; // 同步当前背包的价值 
		backtrack(i+1); // 深度搜索下一层 
		cw-=w[i]; //回溯 
		cp-=v[i]; // 回溯 
	}
	
	// 如若符合条件则搜索右子树 
	if(Bound(i+1)>bestp){
		x[i]=0;
		backtrack(i+1);
	}
		
}


int main(){
	
	knapsack();
	backtrack(1); 
	
	printf("最优价值为：%lf\n",bestp);
    printf("需要装入的物品编号是：");
    for(int i=1;i<=n;i++)
    {
        if(x[i]==1)
            printf("%d ",order[i]);
    }

	return 0;
} 

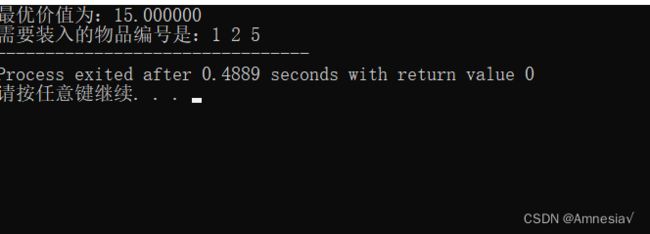
测试结果：

参考：

(12条消息) 【回溯法】－－01背包问题_回溯法求解0-1背包问题_荷叶田田_的博客-CSDN博客

若有侵权，请联系作者删除。

自身的专业水平不高，有什么不足之处，欢迎指正。