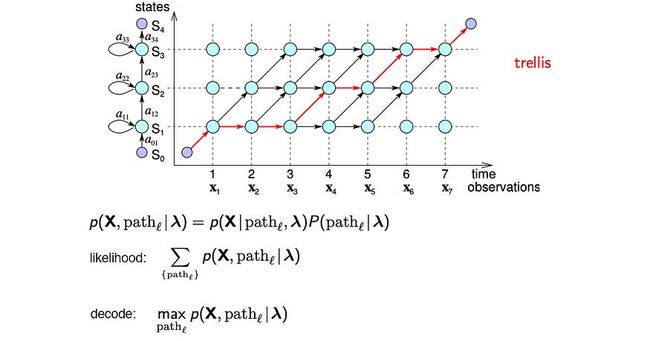
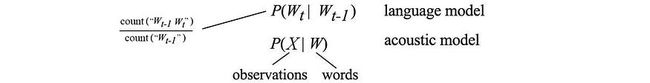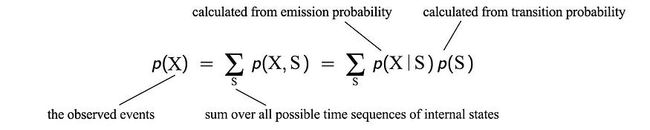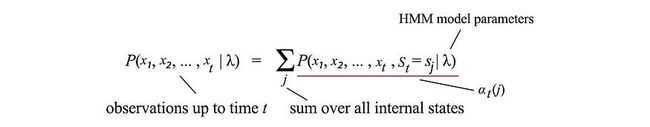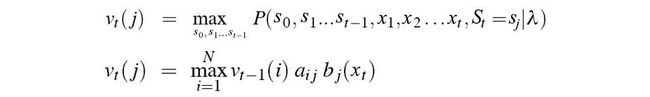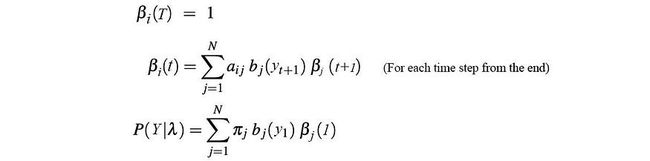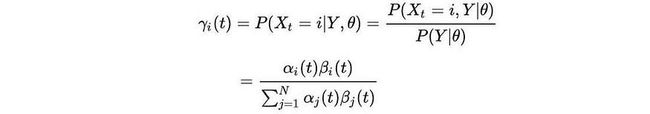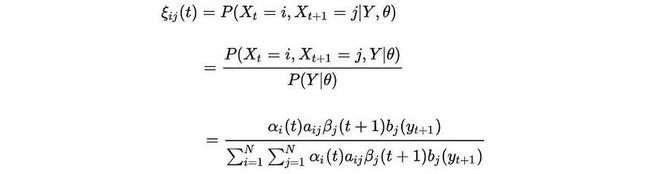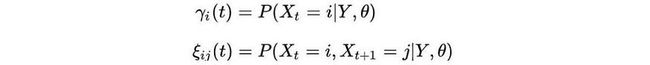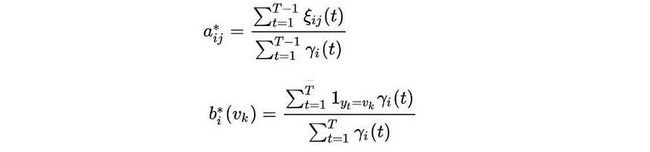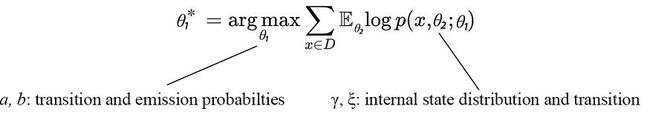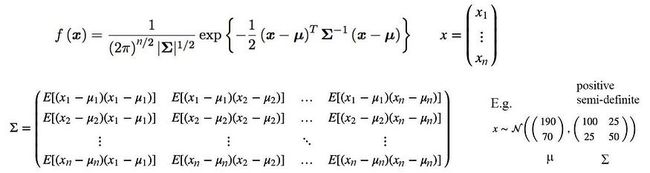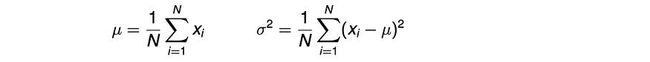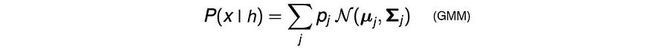【NLP】语音识别 — GMM, HMM
一、说明
在语音识别的深度学习(DL)时代之前,HMM和GMM是语音识别的两项必学技术。现在,有将HMM与深度学习相结合的混合系统,并且有些系统是免费的HMM。我们现在有更多的设计选择。然而,对于许多生成模型来说,HMM仍然很重要。但无论状态如何,语音识别都有助于我们更好地理解HMM和GMM在ML环境中的应用。所以停止长脸,让我们有时花在上面。
二、自动语音识别 (ASR)
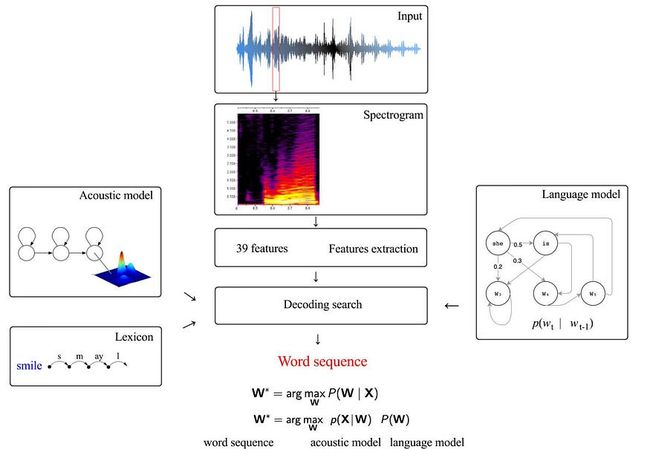
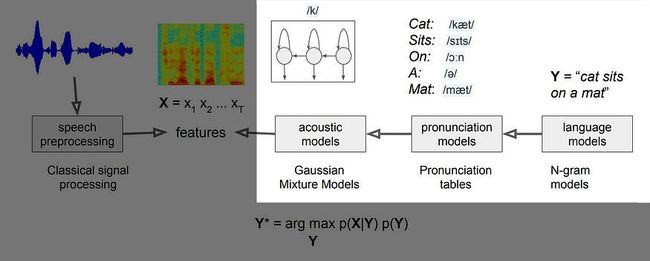
让我们先了解一下高级概述。下图是语音识别的高级体系结构,它将HMM(隐马尔可夫模型)与语音识别联系起来。
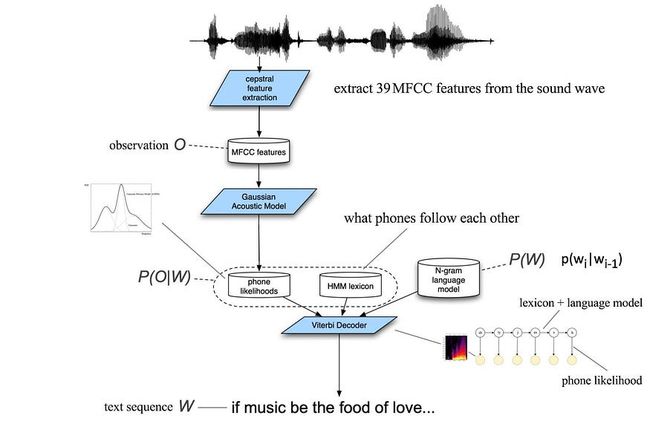
从音频剪辑开始,我们滑动宽度为 25 毫秒、间隔 10 毫秒的窗口以提取 MFCC 特征。对于每个窗口框架,将提取 39 个 MFCC 参数。语音识别的主要目标是构建一个统计模型,从特征向量 X 序列推断文本序列 W(例如“猫坐在垫子上”)。
一种方法查找所有可能的单词序列(最大长度有限),并找到与输入声学特征最匹配的单词序列。
该模型依赖于构建语言模型 P(W)、发音词典模型和声学模型 P(X|W)(生成模型),如下所示。
从源代码修改
发音模型可以使用表格将单词转换为音素,或者语料库已经使用音素转录。声学模型是关于在给定一系列电话而不是单词的情况下对一系列特征向量进行建模。但我们将继续使用符号 p(X|W) 作为声学模型。只是要注意。
语言模型是关于单词序列的可能性。例如,“我看电影”比“我看电影”或“我看苹果”的可能性更大。它根据前面的单词预测下一个单词。如果我们用一阶马尔可夫链近似它,下一个单词将仅取决于当前单词。我们可以通过计算语料库中单词对的出现来估计它。
通过结合声学模型和语言模型,我们搜索具有最大可能性的文本序列。
这种方法听起来很间接,搜索看起来效率低下或不可能。但是p(X|W)在语音识别中建模要容易得多。可以使用高斯混合模型 (GMM) 对电话的特征分布进行建模。我们将通过训练数据来学习它。手机和相应可观测值之间的转换可以使用隐马尔可夫模型 (HMM) 进行建模。因此,如果我们能找到一种有效搜索电话序列的最佳方法,这听起来可能还不错。
HMM 模型由隐藏变量和可观察量组成。下面的顶部节点表示电话,底部节点表示相应的可观察量(音频功能)。水平箭头演示了电话序列中真实标签“她只是......”的过渡。
在语音识别中,可观察量可以用从相应的音频帧中提取的39个MFCC特征来表示。好消息是,使用此HMM模型,我们不需要逐个搜索电话序列。否则,复杂性会随着电话数量的增加呈指数级增长。使用维特比算法或其他HMM方法,我们可以在多项式时间内找到最佳序列。我们稍后会回到这个问题。
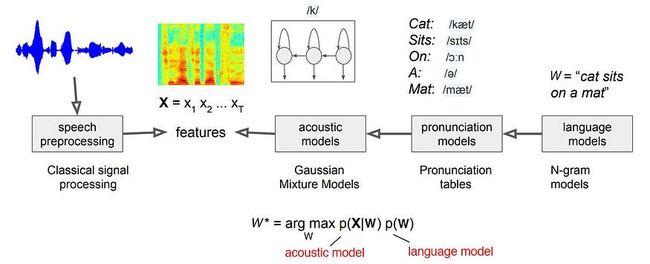
下图是自动语音识别 (ASR) 的可能实现。结合有关词典,声学模型和语言模型的信息,我们可以使用Viterbi解码器找到最佳的电话序列。
从源代码修改(O在这里与X相同)
让我们快速回顾一下,我们可以用HMM对声学模型P(X|W)进行建模。HMM 模型上的箭头将表示电话转换或指向可观察量的链接。为了对我们观察到的音频特征进行建模,我们从训练数据中学习GMM模型。因此,让我们先在一般背景下更多地了解HMM和GMM。
三、隐马尔可夫模型
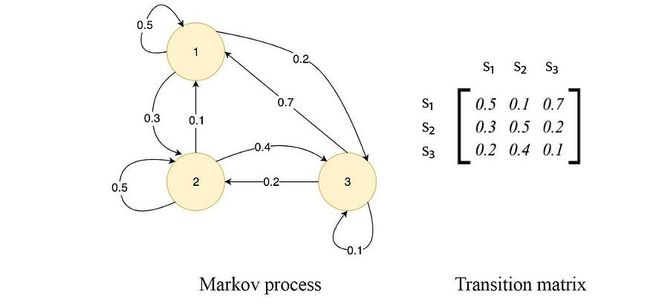
马尔可夫链包含系统的所有可能状态以及从一个状态过渡到另一个状态的概率。
一阶马尔可夫链假设下一个状态仅取决于当前状态。为简单起见,我们通常将其称为马尔可夫链。
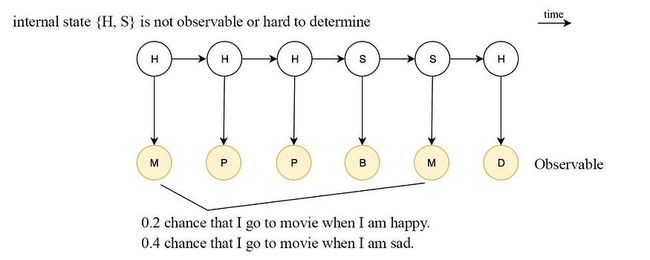
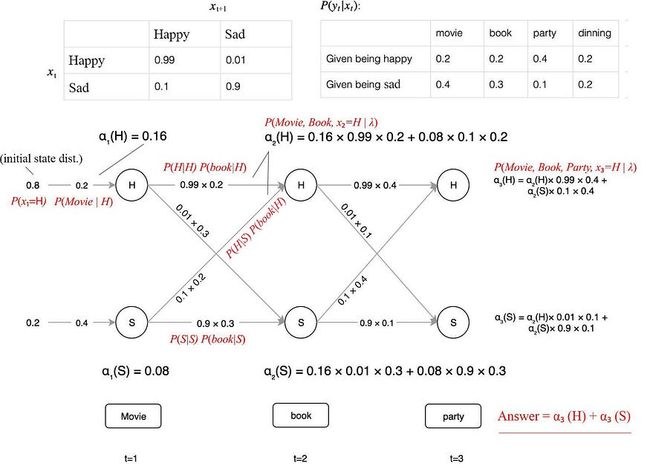
这个模型将更容易处理。然而,在许多 ML 系统中,并非所有状态都是可观察的,我们称这些状态为隐藏状态或内部状态。有些人可能会将它们视为输入的潜在因素。例如,要知道我是快乐还是悲伤可能并不容易。我的内部状态将是 {H 或 S}。但是我们可以从观察中得到一些提示。例如,当我高兴时,我有0.2的机会看电影,但当我悲伤时,这个机会上升到0.4。在给定内部状态的情况下观察可观测物的概率称为发射概率。从一个内部状态过渡到另一个内部状态的概率称为转移概率。
对于语音识别,可观察量是每个音频帧中的内容。我们可以使用 MFCC 参数来表示它。让我们看看我们可以用 HMM 做什么。
前向算法的可能性
HMM 由跃迁和发射概率建模。
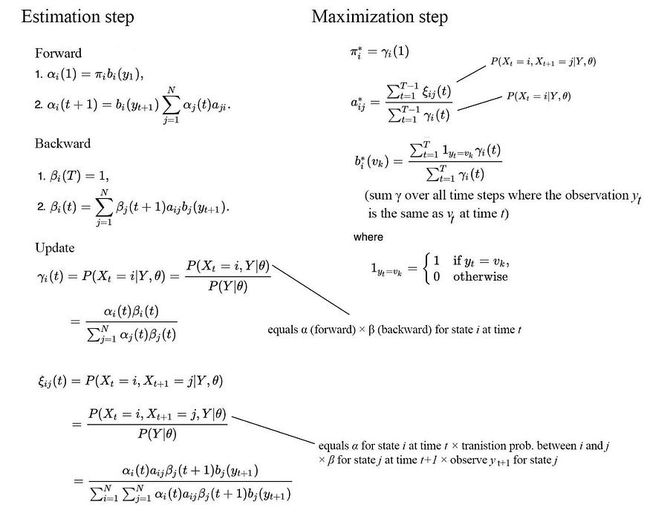
给定学习了HMM模型,我们可以使用前向算法来计算观察的可能性。我们的目标是总结所有可能状态序列的观测概率:
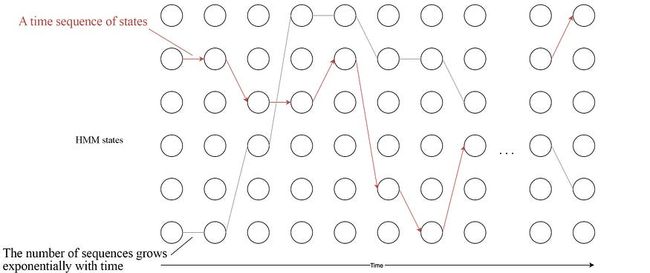
但我们必须聪明地做到这一点。我们不能一次对所有可能的状态序列求和。它具有指数级的复杂性。
我们的策略将采用分而治之的方法。如果我们可以递归地表达计算,我们就可以将问题分解为中间步骤。在 HMM 中,我们使用时间 t-1 和/或 t+1 的结果来解决时间 t 的问题。下面的圆圈代表时间 t 时的 HMM 隐藏状态 j。因此,即使状态序列的数量随时间呈指数增长,如果我们能够随时间递归地表达计算,我们也可以线性求解它。
这是打破指数诅咒的动态编程的思想。在时间 t 处,截至时间 t 的观测概率为:
让我们将红色下划线的项重命名为t(j)(前向概率α并检查我们是否可以递归表示它。由于当前观测值仅取决于当前状态,因此α可以表示为:
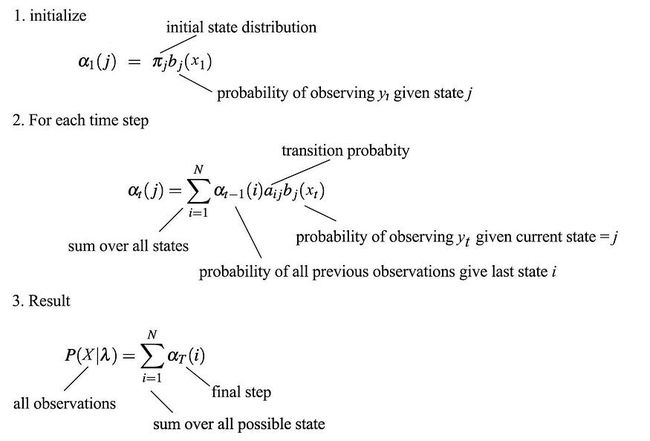
所以它确实有一个递归关系。以下是使用递归计算给定模型 λ 的观测值可能性的步骤。我们不是单独对每个状态序列求和,而是计算从时间步长 1 到结束(时间 T)的α。如果有 k 个内部状态,则复杂度将仅为 O(k²T),而不是指数。
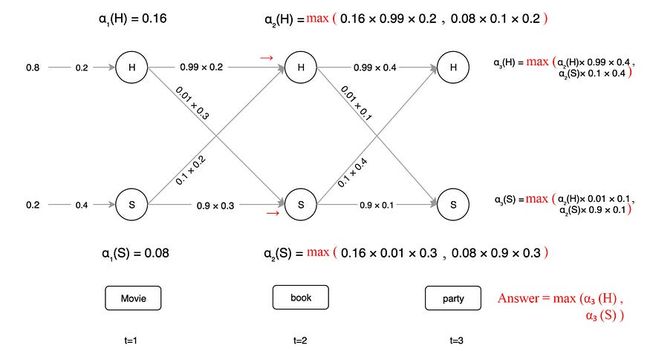
下面是一个示例,我们从左侧的初始状态分布开始。然后我们将α的值向右传播。我们计算每个状态的α,并为每个时间步重复此操作。
接下来,给定HMM模型,我们如何找到给定观察序列的内部状态。此过程称为解码。这对于语音识别尤其有趣。如果我们有一个音频剪辑,则内部状态代表电话。语音识别可以被视为在给定音频剪辑的情况下找到这些内部状态。
解码(查找内部状态 — 维特比算法)
同样,我们希望递归地表达我们的组件。给定时间 t 处的状态为 j,vt(j) 是观测序列与最优状态序列的联合概率。
因此,不仅可以完成,方程类似于前向算法,只是求和被最大函数替换。维特比算法不是在前向算法中对所有可能的状态序列求和,而是采用最可能的路径。
从源代码修改
查找最大化观测值可能性的内部状态类似于似然法。我们只是用最大函数替换求和。
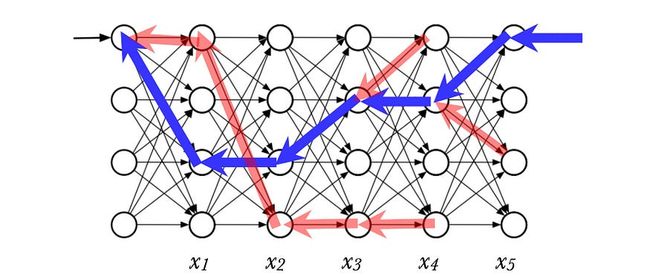
在这个算法中,我们还记录了在时间t(上面的红色箭头)通向每个节点的最大路径,即我们回溯每个节点的最佳路径。例如,我们从 t=1 的快乐状态 H 过渡到 t=2 的快乐状态 H。
源
学习(鲍姆-韦尔奇算法/前向-后向算法)
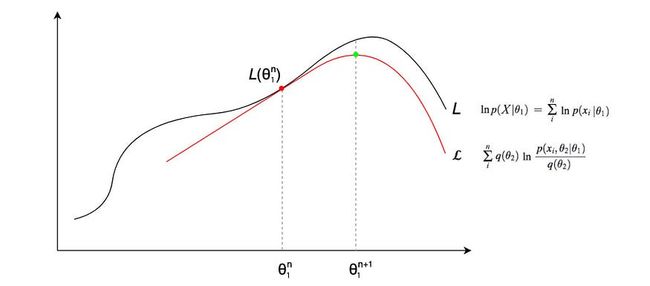
现在,它涉及到困难的部分。我们如何学习HMM模型?这可以通过Baum-Welch算法(前向-后向算法)来完成,以学习跃迁和发射概率。这项任务听起来不可能完成,因为在我们的计算中,这两种概率都非常纠结。但从某种角度来看,如果我们知道状态占用概率(时间t的状态分布),我们就可以推导出发射概率和转移概率。如果我们知道这两个概率,我们可以推导出时间 t 的状态分布。这就是我们在EM算法中讨论的先有鸡还是先有蛋的问题。EM算法在迭代步骤中解决了这个问题。在每一步中,我们优化一个潜在变量,同时修复其他潜在变量。想象一下,每个迭代步骤都会改进解决方案。即使对于连续空间,我们的工作精度也有限,因此,需要探索和改进的是有限的状态。因此,如果我们保持迭代,解决方案将收敛。
因此,鲍姆-韦尔奇算法是EM算法的特例也就不足为奇了。
让我们熟悉以下新符号。
我们已经熟悉前向算法中的α(前向概率)。β(后向概率)是它在相反方向上的近亲(在给定时间 t 的状态 i 的情况下看到所有即将到来的观测值的概率)。我们可以递归地表达它,类似于α但方向相反(又名向后算法)。
要学习HMM模型,我们需要知道我们是什么状态才能最好地解释观察结果。这将是状态占领概率γ — 给定所有观测值的时间 t 的状态 i 的概率。
给定固定的HMM模型参数,我们可以应用前向和后向算法来计算观测值的α和β。γ可以通过简单地将α乘以β来计算,然后重新规范化它。
ξ 是在给定所有观测值的时间 t 之后从状态 i 过渡到 j 的概率。它可以通过类似α和β来计算。
直观地说,使用固定的HMM模型,我们使用给定的观测值细化状态占用概率(γ)和转移(ξ)。
鸡和蛋的部分来了。一旦细化了γ和ξ(θ₂)的分布,我们就可以对最佳跃迁和发射概率(θ₁:a,b)进行点估计。
我们修复一组参数以改进其他参数,并继续迭代,直到解决方案收敛。
EM 算法通常定义为:
在这里,E步建立了p(γ,ξ | x,a,b)。然后,M步长找到a,b,大致最大化下面的目标。
以下是该算法的回顾:
因此,给定训练数据中的所有观察结果,Baum-Welch 算法可以学习 HMM 模型。但是,请记住保持开放的心态。在语音识别中,问题要复杂得多,许多解决方案有时无法很好地扩展。
四、声学模型
从源代码修改
在 ASR 中,我们可以使用发音表为文本序列 Y 生成电话。接下来,我们需要为这些手机创建一个声学模型。
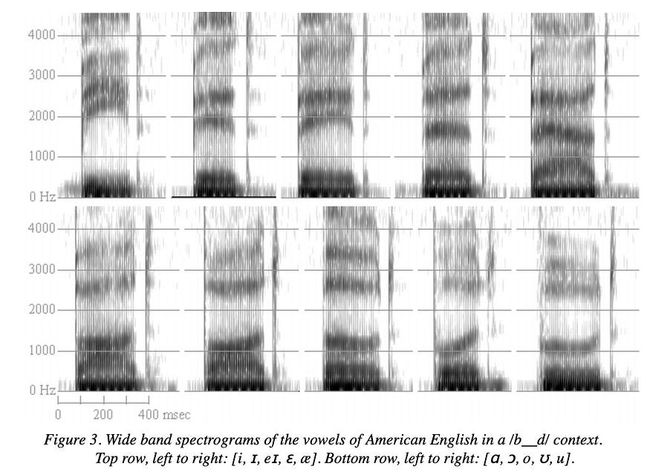
几十年来,人们对语音学的研究已经完成。专家可以通过直接读取频谱图来识别元音和辅音。
源
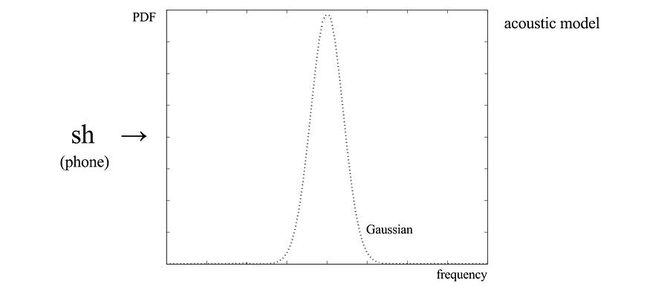
但是同样,我们需要一个更密集的声学模型表示,这样我们就可以确定给定手机P(X|phone)的音频特征向量X的可能性。
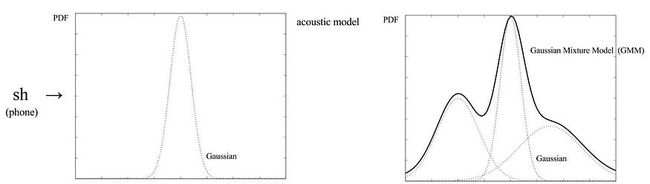
使用 MFCC,我们从音频帧中提取 39 个特征。让我们简化图片,并假设每帧只有一个特征。对于状态“sh”(电话),可以使用正态分布对此功能的值进行建模。
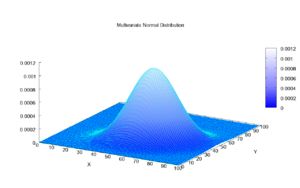
要将概念扩展到 39 个特征,我们只需要一个包含 39 个变量的多元正态分布。下图可视化了两个变量的二元正态分布。
以下是多元正态分布的定义。
其中 Σ 是测量变量之间相关性的协方差矩阵。MFCC 参数具有很好的属性。有相对独立的。因此,Σ的非对角线元素可以简单地设置为零。
但是,多维度思考太难了。因此,我们将坚持使用一维示例进行说明。观测特征 x 的似然 p(x| q) 将计算为它与正态分布 q 的峰值有多远:
给定不同的手机,我们可以计算相应的概率密度值,并将其归类为具有最高值的手机。为了学习这种高斯分布,我们可以简单地从训练数据点xi进行估计。
这些方程可以通过最大化训练数据的可能性来证明。
源
所以这个高斯模型很容易从训练数据中学习,并为我们提供了一个很好的P(x|μ,σ²)。在语音识别的背景下,我们可以学习每部手机的高斯模型(μ,σ²)。这用作可能性概率。这也充当HMM中的发射概率。
不幸的是,即使我们使用多元高斯分布,这个概念也是幼稚的。如果这是真的,学习外语口语会简单得多。这种可能性比单个峰值钟形曲线更复杂。为了解决这个问题,我们切换到高斯混合模型(GMM)。这允许分布是多模态的,即我们允许一个特征有几个可能的值。这提供了语音变体的灵活性。
例如,右侧的GMM将三个具有不同权重的高斯分布组合在一起,形成一个新的概率密度(3分量GMM)。该模型仍然非常密集,6 个高斯参数加上 3 个权重。
直观地,可以在m模式之一附近观察到特定手机的特征值。但某些值可能比其他值更有可能。因此,我们引入权重来指示哪些更有可能。当内部 HMM 状态为 j 时,观察到的特征向量的可能性为:
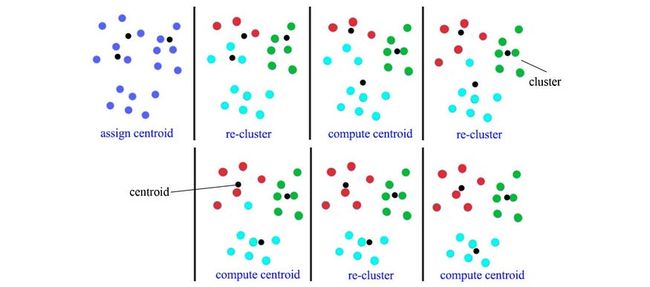
为了学习 GMM,例如对于 2 分量 GMM,我们馈送从训练数据中提取的特征以拟合这两个集群的参数。从概念上讲,我们从这些参数的初始或随机猜测开始。我们找到每个数据样本应属于哪个集群。然后我们根据关联的数据点重新计算聚类参数。
是的,我们将使用 EM 算法迭代解决方案,直到它收敛。在EM中,我们使用软赋值而不是硬赋值。对于硬分配,我们分配每个数据样本所属的特定集群(点估计)。在软赋值中,它将是一个概率分布。因此,样本有可能属于集群。然后,我们根据此软分配重新计算集群参数。由于我们已经多次介绍过这一点,因此我们不会详细说明如何进一步训练它。
回顾一下,给定一部手机,我们可以使用 GMM 学习可观察量的特征向量。这种概率分布允许我们计算给定电话 P(x|s) 的语音片段的可能性——这也是给定 HMM 内部状态的发射概率。
五、矢量量化
在整个过程中,我们尝试对声学信号的更密集表示进行建模。GMM是一种流行的方法。或者,在我们从语料库中提取一组训练的特征向量后,我们将这些特征分组到 k 个聚类中,比如使用 k 均值聚类。这将创建一个大小为 k 的代码本来编码音频帧。
k=3 表示二维数据
有了这个索引,我们可以开始使用它来训练 HMM。训练模型后,我们也可以使用它来解码音频剪辑。这种方法称为矢量量化,并用于早期研究。但与GMM相比,它不太受欢迎。因此,我们只是希望您意识到这一点。
六、反思
GMM 对给定手机的特征向量的观测概率分布进行建模。它提供了一种原则性方法来测量手机和我们观察到的音频帧之间的“距离”。
另一方面,HMM产生了一个关于状态如何过境和观察的原则模型。由于观测值的概率可以用HMM建模为:
方程源
其中 h 是隐藏状态(电话)。给定手机功能的可能性可以使用GMM建模。