javaSE 数组的定义与使用
文章目录
- 一、数组是什么?
- 二、数组的使用
-
- 2.1创建与初始化
-
- 动态初始化
- 静态初始化
- 2.2数组的使用
- 2.3遍历数组
-
- 索引从0开始的原因
- 数组越界
- 两种遍历数组的区别
- 三、数组作为引用数据类型
-
- 3.1数组作为方法参数
- 3.2引用数据类型的理解(重难点)
-
- 练习 实现一个copyOf的方法
- 3.3认识null
- 四、数组练习
-
- 4.1数组转换为字符串
- 4.2数组copyOf方法
- 4.3找数组中最大元素
- 4.3二分查找(重点)
-
- 二分查找(递归思路)
- 4.4判断是否是一个有序数组(重点,找反例)
- 4.5冒泡排序(重点)
-
- 优化冒泡排序(易错点)
- 4.6数组逆序
- 4.7数组的数字排列问题(重难点,双引用)
- 五、数组面试题(简单)
-
- 5.1 leetcode两数之和
- 5.2 leetcode136 只出现一次的数字
- 5.3 leetcode169 多数元素
-
- 摩尔投票法(重点掌握)
- 5.4 leetcode1550 存在三个连续奇数
一、数组是什么?
一次定义N个相同数据类型的变量,我们就把这种结构称之为数组。
在Java中, 数组中包含的变量必须是相同类型
二、数组的使用
2.1创建与初始化
动态初始化
静态初始化
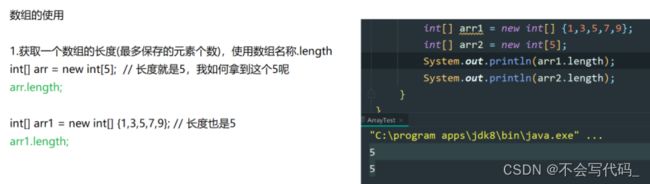
2.2数组的使用
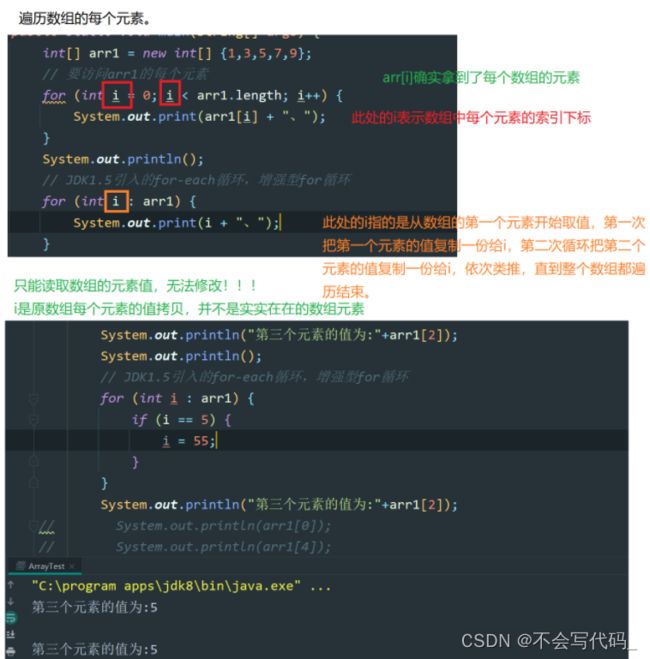
2.3遍历数组
索引从0开始的原因
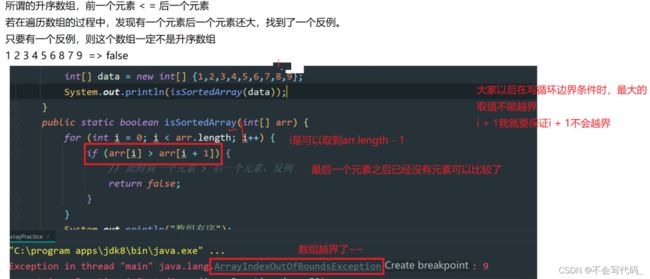
数组越界
下标访问操作不能超出有效范围 [0, length - 1] , 如果超出有效范围, 会出现下标越界异常。

两种遍历数组的区别
注意事项:1.for循环遍历数组,边界条件一定不能取到arr.length
2.for循环的i是索引下标,for-each中的i是个临时变量
3.for-each拿到的数组元素不能被修改,for循环可以修改
三、数组作为引用数据类型
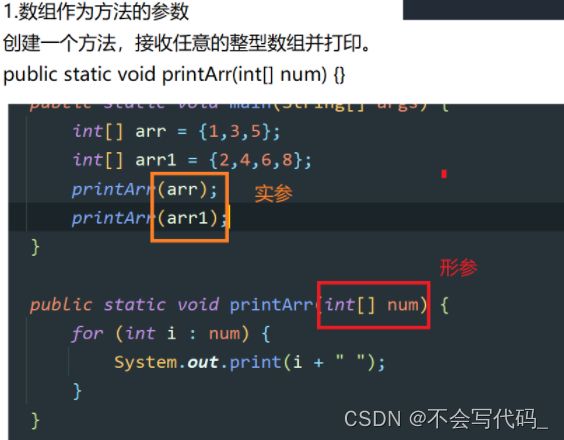
3.1数组作为方法参数
3.2引用数据类型的理解(重难点)

注意事项:方法中的局部变量和形参都在栈中存储
方法调用结束就会出栈,例如下图中的蓝色方框swap方法
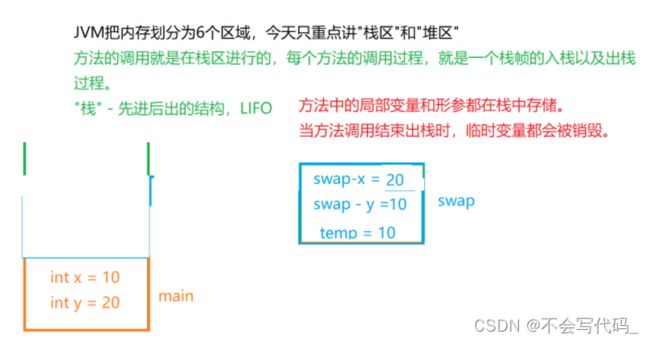
数组引用:

创建的对象都在堆中,实实在在存在的,引用名称是保存在栈中的,里面保存元素存储的地址。此时调用swapArr方法,压入栈中,里面也保存指向堆内存数组的地址。
数组引用进阶:此时swap方法中传递的形参还是main方法中arr在堆内存中的地址了(图中紫色箭头所示),但是传入在swap方法中arr又指向new的新对象的地址(图中红色横线所示),swap里的arr和mian方法中的arr虽然数值和名称相同,但是是两个完全不同的对象(新对象就是堆内存中的灰色方框)。所以此时swap交换的并不是main方法的arr。当方法调用结束后,swap中arr引用就释放了(图中紫色方框弹出栈顶)但是对象还存在。详情看图中的内存情况。
记住:看见new关键字,一定在堆内存开辟了一个新的空间

解决方法:swap方法修改返回值类型为整形数组,并且最后return交换的数组返回main方法中,main方法中用一个新入栈的ret引用接收。
内存分析:在栈中压入一个swap中的arr引用指向新地址(0x300)。交换后的地址(0x300)交给压入栈中的新引用ret。方法调用结束后swap中arr就弹出栈顶。


练习 实现一个copyOf的方法
//实现一个copyOf方法
public static int[] copyOf(int[] arr){
int[] newArr=new int[arr.length];
for (int i = 0; i < arr.length; i++) {
newArr[i]=arr[i];
}
return newArr;
}
如何证明新数组不是原来的数组?
只需要修改原数组arr【0】=一个新的val,再打印原数组,看看val是否发生变化即可。

内存分析:方法内部创建新数组,和原数组大小,内容完全相同,只是堆内存地址不同。
3.3认识null
null 在 Java 中表示 “空引用” , 也就是一个无效的引用
int[] arr = null;
System.out.println(arr[0]);
// 执行结果 Exception in thread "main" java.lang.NullPointerException at Test.main(Test.java:6)
四、数组练习
4.1数组转换为字符串
//自己实现一个toString方法
public static String arr2String(int[] arr){
String str="[";
for (int i = 0; i < arr.length; i++) {
str+=arr[i];
//最后一个要特殊处理,不加逗号
if(i!= arr.length-1){
str+=",";
}
}
return str;
}
4.2数组copyOf方法
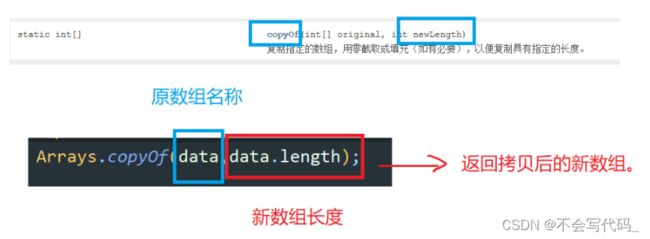
当拷贝的新数组小于原数组长度时:

当拷贝的新数组大于原数组长度时:
注意是默认值,不是0,比如double就是0.0!
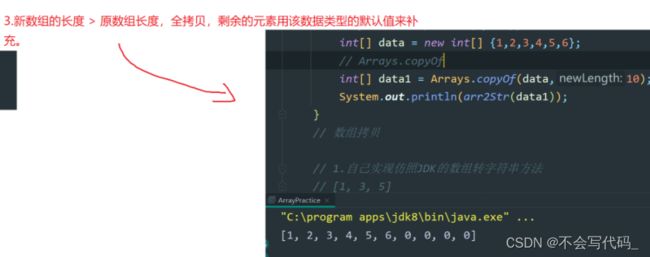
补充:数组的区间拷贝

4.3找数组中最大元素
public static int max(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return max;
}
4.3二分查找(重点)
条件:只能在有序的数组中才可以使用
绿色字体为二分查找的基本思想

循环的终止条件:
一定是left小于等于right
如果left==right,这个索引位置一定还有一个元素

还需要注意int mid一定是在while循环内定义的,每次循环左边界或者右边界都会发生变化
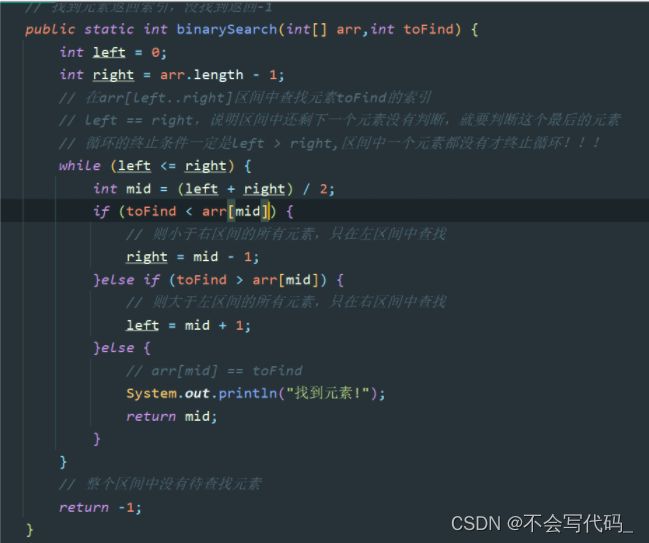
二分查找是一个对数级别算法:

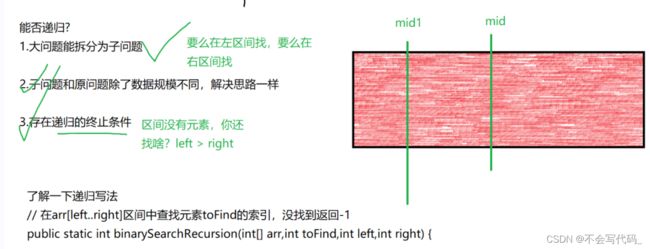
二分查找(递归思路)
/**
* 进阶-递归二分查找
* 语义:在数组data的区间left--right中查找目标元素val,返回数组下标
* */
public static int binaryRecursion(int[] data,int val,int left,int right){
//边界条件
if(left>right){
//空区间找不到,直接返回-1;
return -1;
}
int mid=(left+right)/2;
if(data[mid]==val){
return mid;
}else if(val<data[mid]){
//小于区间右侧元素
//根据语义:剩下的做区间交给子方法去找
return binaryRecursion(data,val,left,mid-1);
}
//同理
return binaryRecursion(data,val,mid+1,right);
}
4.4判断是否是一个有序数组(重点,找反例)
易错点:循环边界条件一定是arr.length-1,保证i+1(最大值)不可以越界
/* *
* 判断数组是否有序
* */
public static boolean isSortArray(int[] data){
for (int i = 0; i < data.length-1; i++) {
if(data[i]>data[i+1]){
//找到一个反例
return false;
}
}
return true;
}
4.5冒泡排序(重点)
代码示例:
/**
* 冒泡排序
* */
public static void bubbleSort(int[] data){
//待排序的元素,就是数组内所有元素,排好一个就加一个
for (int i = 0; i < data.length; i++) {
//当前元素需要比较的次数
//-1是为了防止比较时数组越界
//-i可以理解为减去已经排好的元素
for (int j = 0; j < data.length-1-i; j++) {
//比较前一个元素与后一个元素
if(data[j]>data[j+1]){
int temp=data[j];
data[j]=data[j+1];
data[j+1]=temp;
}
}
}
}
易错点:
第二个for循环-1就是为了防止数组越界(参照4.4判断数组是否有序),-i则是理解为减去已经排序好的元素个数。
优化冒泡排序(易错点)
第一个优化点:arr.length-1 减少一个待排序的元素,因为前面所有元素排序之后,剩下的最后一个元素一定是已经排序好了(自己画个图),不用再去遍历数组
第二个优化点:如果一个数组已经是有序数组了,可以在每次内层for循环元素比较之前加个标志符boolean变量,并初始化为true。最后比较完之后如果状态标志符不变,说明已经是有序数组,没有进入倒数第二个if语句进行比较,,第二个for循环结束后,进入最后一个if语句提前结束。

/**
* 冒泡排序优化
*/
public static void bubbleSort1(int[] data) {
for (int i = 0; i < data.length-1; i++) {
//当前元素需要比较的次数
//-1是为了防止比较时数组越界
//-i可以理解为减去已经排好的元素
boolean isSwapped = true;
for (int j = 0; j < data.length - 1 - i; j++) {
//比较前一个元素与后一个元素
if (data[j] > data[j + 1]) {
isSwapped = false;
int temp = data[j];
data[j] = data[j + 1];
data[j + 1] = temp;
}
}
//只有等于ture才可以进入if语句
//所以要保证isSwapped一直等于true才可以
//保证的前提就是不进入if语句(已经有序的数组)
if (isSwapped) {
break;
}
}
}
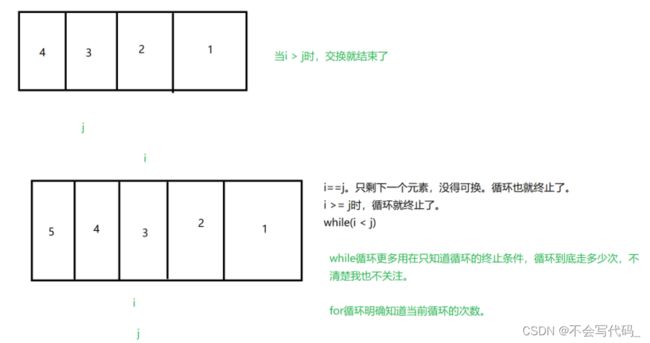
4.6数组逆序
注意事项:通过奇数个和偶数个元素数组我们发现,循环的终止条件就是i>=j
/**
* 数组逆序
* */
public static void reverse(int[] data){
int i=0;
int j= data.length-1;
while (i<j){
int temp=data[i];
data[i]=data[j];
data[j]=temp;
i++;
j--;
}
}
4.7数组的数字排列问题(重难点,双引用)
核心思路:双引用,两个下标分别指向第一个元素和最后一个元素。用前一个下标从左往右找到第一个奇数, 用后一个下标从右往左找到第一个偶数, 然后交换两个位置的元素。
易错点:可能数组中存在全是奇数或者全是偶数的情况,所以即使在遍历过程中(代码示例中第二、三个while循环),也必须保证i
/**
* 数字排列问题:偶数在前,奇数在后
* */
public static void transform(int[] data){
int i=0;
int j= data.length-1;
//i和j相等时,不管是奇数还是偶数都可以不用交换了
while(i<j){
//从前遍历找奇数,所以循环条件就是遇到偶数向后遍历
while(i<j&&data[i]%2==0){
i++;
}
//走出循环说明此时data[i]遇到了奇数
//从后往前遍历寻找偶数,所以循环条件就是遇到奇数一直向前遍历
while (i<j&&data[j]%2!=0){
j--;
}
//走出循环说明此时data[j]一定是个偶数
//交换三连
int temp=data[i];
data[i]=data[j];
data[j]=temp;
//易错点
i++;
j--;
}
}
五、数组面试题(简单)
5.1 leetcode两数之和
添加链接描述
易错点:不能返回同一个索引,所以终止条件是j>i
public int[] twoSum(int[] nums, int target) {
int[] ret=new int[2];
for (int i = 0; i < nums.length; i++) {
//从后向前,终止条件是当j<=i停止
for (int j = nums.length-1; j >i ; j--) {
if(nums[i]+nums[j]==target){
ret[0]=i;
ret[1]=j;
return ret;
}
}
}
return null;
}
5.2 leetcode136 只出现一次的数字
添加链接描述
易错点:
第一个:int count定义的位置
第二个:内层for循环的起始值(不可以等于i)

public int singleNumber(int[] nums) {
for (int i = 0; i < nums.length; i++) {
//统计每个数字出现的次数
//一定要定义在第一个for循环之内
//每遍历一个数字之前,要把之前数字出现次数置为0
int count=0;
//第二个for循环也必须从头开始遍历
for (int j = 0; j < nums.length; j++) {
if(nums[i]==nums[j]){
count++;
}
}
if(count==1){
return nums[i];
}
}
return -1;
}
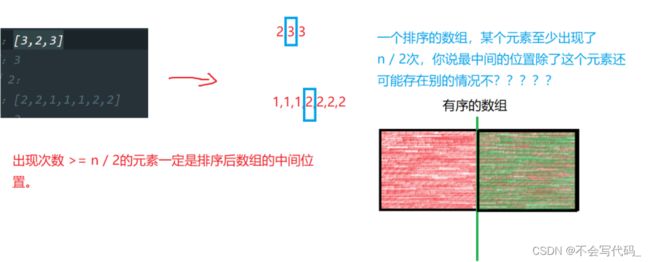
5.3 leetcode169 多数元素
添加链接描述
核心思路:属于技巧类型的题目,如果给数组排序,这个多数元素,一定位于排序后的arr.length/2的索引位置处
public int majorityElement(int[] nums) {
Arrays.sort(nums);
return nums[nums.length/2];
}
}
摩尔投票法(重点掌握)
时间效率比上面的高,摩尔投票法是O(n),上面的是nlogN
核心思路:一样的数字加1,不一一样的数字减1,相当于一对一抵消了,而且遍历一次就结束得出答案。只要计数器变成了0,就要换候选人,换成当前遍历到的元素

public int majorityElements(int[] nums) {
//摩尔投票法
//首先让第一个元素当候选人
int candidate=nums[0];
//新候选人总会给自己投一票,所以count==1
int count=1;
for (int i = 1; i < nums.length; i++) {
if(nums[i]==candidate){
count++;
}else {
count--;
}
if(count==0){
//更换候选人
candidate=nums[i];
count=1;
}
}
//遍历结束后一定是count>=1的元素(出现次数最多的)
return candidate;
}
}
5.4 leetcode1550 存在三个连续奇数
添加链接描述
易错点:第二个if语句要包含在第一个if语句中,题目要求是连续的三个奇数,连续相加等3就可以返回。但只要遇到偶数,直接让计数器count=0,重现开始计数。
/**
* 存在三个连续奇数
* */
public boolean threeConsecutiveOdds(int[] arr) {
int count=0;
for (int i = 0; i < arr.length; i++) {
if (arr[i] % 2 != 0) {
count++;
if (count == 3) {
return true;
}
} else {
count = 0;
}
}
return false;
}
}