【数据结构】二叉树前中后层序遍历代码实现以及各种操作与二叉树OJ题目
目录
一、二叉树的遍历
1、前序遍历
2、后续遍历
3、中序遍历
二、二叉树简单的操作
1、计算节点个数
1.二叉树所有节点个数
2.二叉树叶子节点个数
3.二叉树第K层节点个数
2、二叉树的高度
3、二叉树是否存在key
1.二叉树中是否存在key
2.寻找二叉树中key节点
三、二叉树OJ题目
1、力扣OJ：相同的树
2、力扣OJ：另一颗树的子树
3、力扣OJ：平衡二叉树
4、力扣OJ：对称二叉树
5、力扣OJ：层序遍历
6、牛客OJ：完全二叉树
一、二叉树的遍历
1、前序遍历
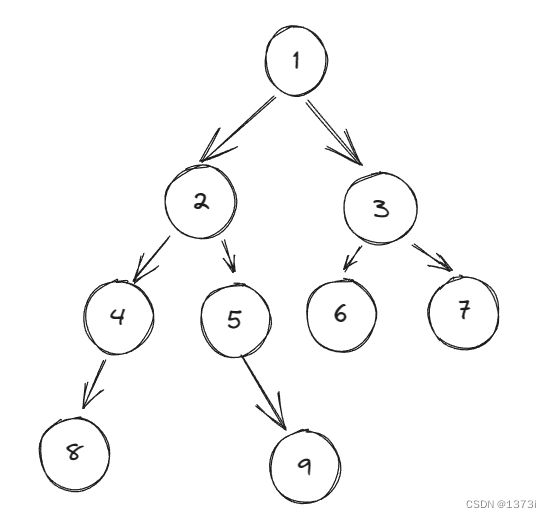
二叉树的前序遍历，顾名思义就是将根节点放在最前面进行遍历，也就是先遍历跟节点，然后再遍历左节点，最后右节点。如下图，按照前序遍历对这棵树进行遍历，我们先要遍历跟节点，然后左子树最后右子树 1-》2 -》4 -》8 -》5 -》9 -》 3 -》6 -》 7
144. 二叉树的前序遍历 - 力扣（LeetCode）
https://leetcode.cn/problems/binary-tree-preorder-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List preorderTraversal(TreeNode root) {
// 1. 创建List
List res = new ArrayList<>();
// 2. 判断如果为空则直接返回
if (root == null) {
return res;
}
// 3. 先将根节点的值存入List
res.add(root.val);
// 4. 再去遍历他的左子树，将遍历的结果存入List
res.addAll(preorderTraversal(root.left));
// 5. 最后遍历右子树，再将结果存入List
res.addAll(preorderTraversal(root.right));
// 6. 最后返回
return res;
}
} 2、后序遍历
与前序遍历不同的是后序遍历是先遍历左节点然后右节点最后遍历根节点
145. 二叉树的后序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-postorder-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List postorderTraversal(TreeNode root) {
// 1. 创建List
List res = new ArrayList<>();
// 2. 如果根节点为空则直接返回
if (root == null) {
return res;
}
// 3. 遍历左子树并将结果存入List
res.addAll(postorderTraversal(root.left));
// 4. 遍历右子树并将结果存入List
res.addAll(postorderTraversal(root.right));
// 5. 最后遍历根节点
res.add(root.val);
// 6. 返回List
return res;
}
} 3、中序遍历
中序遍历就是先遍历左节点，然后遍历根节点，最后再遍历右节点
94. 二叉树的中序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-inorder-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List inorderTraversal(TreeNode root) {
// 1. 创建List存储数据
List res = new ArrayList<>();
// 2. 如果根节点为空则直接返回res
if (root == null) {
return res;
}
// 3. 先遍历左子树，将左子树的数据存入List
res.addAll(inorderTraversal(root.left));
// 4. 再遍历根节点
res.add(root.val);
// 5. 最后遍历右子树
res.addAll(inorderTraversal(root.right));
// 6. 返回数据
return res;
}
} 二、二叉树简单的操作
1、计算节点个数
1.二叉树所有节点个数
在计算节点个数的时候，采用子问题法将二叉树看作若干个子二叉树，则节点个数=当前节点的左子树个数+右子树节点个数+1，此时我们只需要进行递归遍历即可
public int size(TreeNode root) {
// 1. 如果根节点为空则返回0
if (root == null) {
return 0;
}
// 2. 节点个数 = 左子树节点个数 + 右子树节点个数 + 1（自身）
return size(root.left) + size(root.right) + 1;
}2.二叉树叶子节点个数
与上树不同的是，我们只需计算叶子节点个数即可，那么叶子节点有什么特点呢，他的左右节点都为null，根据这一特点，我们可以知道一颗二叉树的叶子节点个数就 = 左子树叶子节点个数 + 右子树叶子节点个数
public int leafSize(TreeNode root) {
// 1. 如果根节点为空则返回0
if (root == null) {
return 0;
}
// 2. 如果该节点是叶子节点 则返回0
if (root.left == null && root.right == null) {
return 1;
}
// 3. 叶子节点 = 左子树叶子节点个数 + 右子树叶子节点个数
return leafSize(root.left) + leafSize(root.right);
}3.二叉树第K层节点个数
我们在遍历整个树的过程中，第k层节点的个数 = 左子树第k层的个数 + 右子树第k层的个数
public int getKSize(TreeNode root, int k) {
// 1. 如果根节点是空则返回0
if (root == null) {
return 0;
}
// 2. 如果此时是第k层节点，则返回1
if (k == 1) {
return 1;
}
// 3. 第k层节点个数 = 左子树k层个数 + 右子树k层个数
return getKSize(root.left,k - 1) + getKSize(root.right, k - 1);
}2、二叉树的高度
二叉树的高度其实就是左子树与右子树两个树的最大高度+1，而左子树的高度也就是左子树的左子树与左子树的右子树高度最大值+1
public int height(TreeNode root) {
// 1. 如果根节点为空则返回0
if (root == null) {
return 0;
}
// 2. 树的高度 = max（左子树高度，右子树高度） + 1
return Math.max(height(root.left),height(root.right)) + 1;
}3、二叉树是否存在key
1.二叉树中是否存在key
二叉树中是否存在key，我们可以在遍历的时候进行判断，如果存在则返回，只要左子树或者右子树中的一个有就存在
public boolean contains(TreeNode root, int key) {
// 如果根节点为空，则返回false
if (root == null) {
return false;
}
// 如果相同则存在
if (root.val == key) {
return true;
}
return contains(root.left,key) || contains(root.right,key);
}2.寻找二叉树中key节点
在上面操作的基础上，我们如果发现这个节点后可直接将该节点进行返回
public TreeNode find(TreeNode root, int key) {
// 1. 如果根节点为空则不存在
if (root == null) {
return null;
}
// 2. 如果找到则直接返回该节点
if (root.val == key) {
return root;
}
// 3. 遍历左子树寻找该节点
TreeNode left = find(root.left,key);
if (left != null) {
// 3.1 找到则返回
return left;
}
// 4. 遍历右子树寻找该节点
TreeNode right = find(root.right,key);
if (right != null) {
// 4.1 找到则返回
return right;
}
// 5. 走到此处说明左子树与右子树都没有，则返回null
return null;
}三、二叉树OJ题目
1、力扣OJ：相同的树
100. 相同的树 - 力扣（LeetCode）https://leetcode.cn/problems/same-tree/
判断两颗二叉树是否相同，我们只需在遍历时判断这两棵树是否相同，可能存在以下几种情况 
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
// 1. 如果都为空则相同
if (p == null && q == null) return true;
// 2. 如果一个有节点 一个没有则不相同
if (p == null && q != null || q == null && p != null) return false;
// 3. 如果节点的值不同,则两个树不相同
if (p.val != q.val) return false;
// 4. 此时说明根节点相同，还需要满足左子树相同并且右子树也相同
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
}2、力扣OJ：另一颗树的子树
572. 另一棵树的子树 - 力扣（LeetCode）https://leetcode.cn/problems/subtree-of-another-tree/
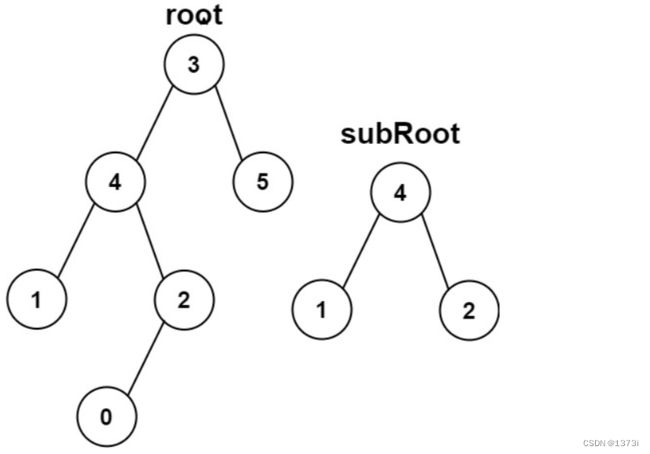
我们需要拿着子树与二叉树的根节点进行比较，看是否是相同的树，如果不是则与他的左子树进行比较，如果也不是则与他的右子树进行比较，以此类推，所有此处我们需要使用上一题的代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSameTree(TreeNode p,TreeNode q) {
// 1. 如果都为空则相同
if (p == null && q == null) return true;
// 2. 如果一个有节点 一个没有则不相同
if (p == null && q != null || q == null && p != null) return false;
// 3. 如果节点的值不同,则两个树不相同
if (p.val != q.val) return false;
// 4. 此时说明根节点相同，还需要满足左子树相同并且右子树也相同
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
// 1. 如果两个树其中一个是空则返回false
if (root == null || subRoot == null) return false;
// 2. 只要他与根节点 或者 左子树 或者 右子树 其中一个树相同，则他就是子树
return isSameTree(root,subRoot) || isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot);
}
}3、力扣OJ：平衡二叉树
110. 平衡二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/balanced-binary-tree/
以下是对平衡二叉树的定义
那么判断一棵树是否是平衡二叉树，只需要根节点是平衡二叉树且他的左右子树都是平衡二叉树即可，因为需要判断左右子树的高度差，所有我们需要将前面求树的高度的代码用在此处
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
return Math.max(maxDepth(root.left),maxDepth(root.right)) + 1;
}
public boolean isBalanced(TreeNode root) {
// 1. 如果根节点为空则返回真
if (root == null) {
return true;
}
// 2. 根节点满足 && 左右子树满足
return Math.abs(maxDepth(root.left) - maxDepth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
}但是上述代码的时间复杂度O(n^2)，那么可以优化上述代码吗，我们在上述代码中在求左右子树高度的时候其实可以在递归遍历的时候进行处理，当求高度递归过程中发现存在根节点的左右子树高度差不满足<=1时就可返回一个负值表示，该二叉树中存在不平衡的子树，进而根据求高度时的返回值来判断是否是平衡二叉树了。这种实现方式时间复杂度则为O(n)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int maxDepth(TreeNode root) {
// 1. 如果根节点为空则高度为0
if (root == null) {
return 0;
}
// 2. 计算左右子树高度
int left = maxDepth(root.left);
int right = maxDepth(root.right);
// 3. 判断是否满足平衡二叉树
if (left != -1 && right != -1 &&Math.abs(left - right) <= 1) {
return Math.max(left,right) + 1;
} else {
// 3.1 不满足则返回-1
return -1;
}
}
public boolean isBalanced(TreeNode root) {
// 1. 如果根节点为空则返回真
if (root == null) {
return true;
}
// 2. 根据求高度时返回值判断
return maxDepth(root) >= 0;
}
}4、力扣OJ：对称二叉树
101. 对称二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/symmetric-tree/
我们只需要判断根节点的左右子树是否对称即可
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
// 1. 处理特殊情况
if (root == null) {
return true;
}
// 2. 只要左子树与右子树对称即可
return isSymmetric(root.left,root.right);
}
private boolean isSymmetric(TreeNode root1,TreeNode root2) {
// 1. 如果两颗树都为空则对称
if (root1 == null && root2 == null) return true;
// 2. 如果一棵树为空另一颗树不为空则不对称
if (root1 == null && root2 != null || root1 != null && root2 == null) return false;
// 3. 如果值不相同也不对称
if (root1.val != root2.val) return false;
// 4. 最后递归判断root1的左子树与root2的右子树，root1的右子树与root2的左子树是否相同
return isSymmetric(root1.left,root2.right) && isSymmetric(root1.right,root2.left);
}
}5、力扣OJ：层序遍历
102. 二叉树的层序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-level-order-traversal/二叉树的层序遍历，此处我们使用队列来进行处理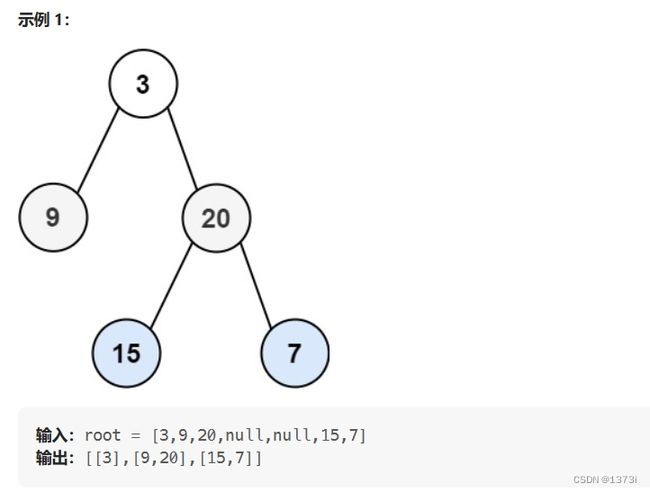
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List> levelOrder(TreeNode root) {
// 1. 如果根节点为空则直接返回
List> res = new ArrayList<>();
if (root == null) {
return res;
}
// 2. 将根节点存入队列
Queue queue = new LinkedList<>();
queue.offer(root);
// 3. 循环处理
while (!queue.isEmpty()) {
// 3.1 计算该层元素个数
int size = queue.size();
List row = new ArrayList<>();
// 3.2 开始将该层元素存入row，并将下一层元素存入queue
while (size-- != 0) {
// 3.2.1 弹出队顶元素
TreeNode top = queue.poll();
// 3.2.2 将值存入row
row.add(top.val);
// 3.2.3 将下一层节点存入queue
if (top.left != null) queue.offer(top.left);
if (top.right != null) queue.offer(top.right);
}
// 3.3 将row存入res
res.add(row);
}
// 4. 返回
return res;
}
} 6、牛客OJ：完全二叉树
判断是不是完全二叉树_牛客题霸_牛客网 (nowcoder.com)https://www.nowcoder.com/practice/8daa4dff9e36409abba2adbe413d6fae?tpId=196&tqId=39379&ru=/exam/oj
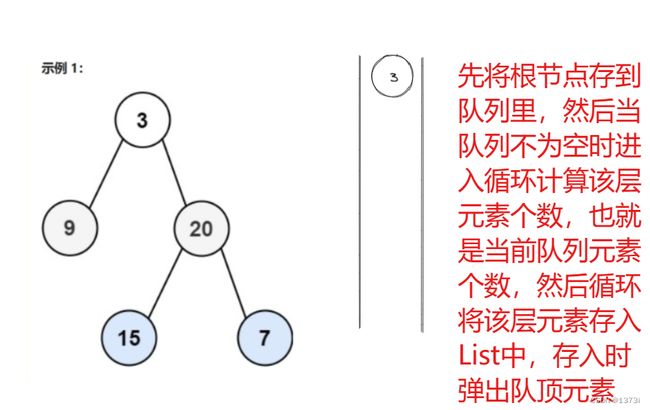
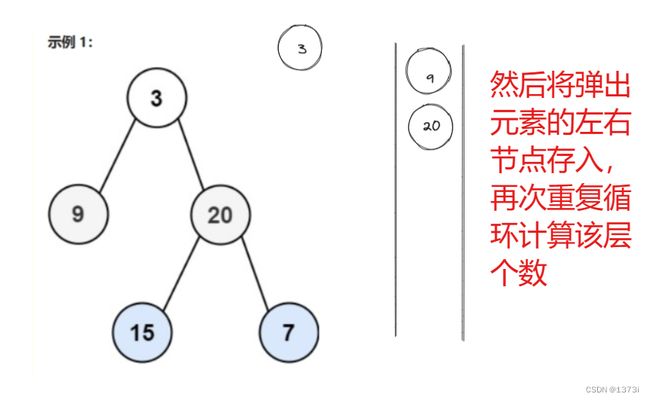
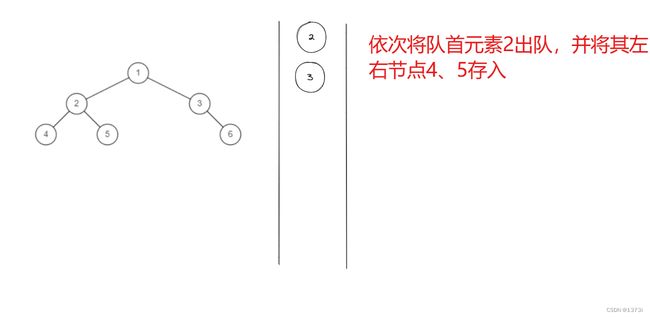
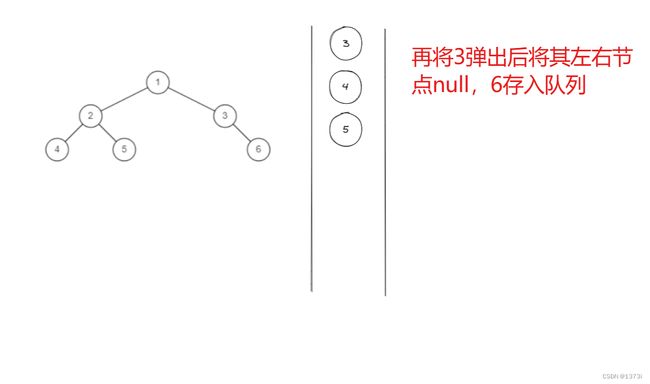
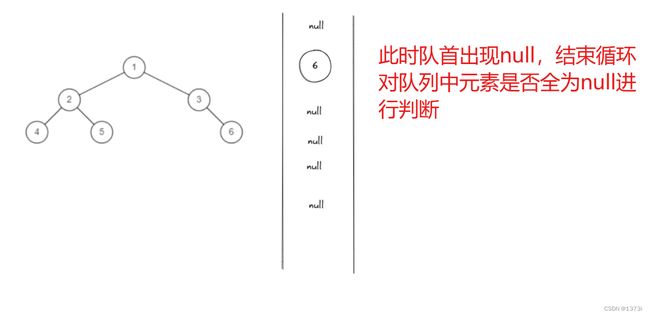
以上是对完全二叉树的定义，我们此处也可以使用队列来处理，按照层序遍历的方法进行处理，不过在存入根节点的左右子树时不进行null值判断，也就是将null值也存入，最后通过判断队列里的元素是否全是null来判断是否是完全二叉树，如果是完全二叉树，按照层序遍历方式处理完队列中剩余元素全是null，而如果不是完全二叉树则不仅仅只要null 
上述 以不完全二叉树进行举例，可将完全二叉树进行上述操作，发现结果中队列里全为null
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
public boolean isCompleteTree (TreeNode root) {
// 1. 特殊处理
if (root == null) {
return true;
}
// 2. 创建队列，将根节点存入队列
Queue queue = new LinkedList<>();
queue.offer(root);
// 3. 开始操作
while (!queue.isEmpty()) {
// 3.1 弹出队首元素
TreeNode top = queue.poll();
if (top != null) {
// 3.1.2 将左右节点存入
queue.offer(top.left);
queue.offer(top.right);
} else {
// 3.1.3 出现null 结束循环
break;
}
}
// 4. 开始判断队列中是否全是null
while (!queue.isEmpty()) {
TreeNode top = queue.peek();
if (top != null) {
return false;
} else {
queue.poll();
}
}
return true;
}
} 后续题目正在补充中……