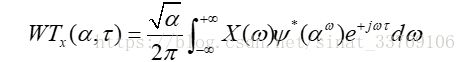二维小波变换在图像降噪与压缩中的应用

1 介绍

图像中包含了人类感知世界、认识世界、改造世界的大部分信息量。图像处理就是对图像信息进行加工处理，以满足人的视觉心理和实际应用的要求。图像去噪是图像处理研究的一个永恒主题。大多数图像去噪的方法,尤其是高斯白噪声的去噪方法,从本质上来说,都是低通滤波的方法. 低通滤波是一把双刃剑,它在消除图像噪声的同时,也会消除图像部分有用的高频信息. 因此,各种图像去噪方法,其实就是在去噪和保留有用高频信息之间进行权衡.

图像的小波阈值去噪方法[1]是众多图像去噪方法的佼佼者,它利用图像小波分解后,各个子带图像的不同特性,选取不同的阈值,从而达到较好的去噪效果.但是,它也同样受到去噪和保留有用高频信息两难的困扰.

边缘特征是图像最为有用的高频信息. 根据视觉生理和心理学研究的结果,边缘特征是视觉系统最能强烈感受到的少数几个图像特征之一[2] ,因此,在图像去噪的同时,尽量保留图像的边缘特征,应是图像去噪首要顾及的问题.

基于边缘检测的小波图像阈值去噪方法,在阈值去噪之前,先通过小波边缘检测,确定边缘特征在各个子带图像中的位置,而在这些位置上的小波系数将不受阈值去噪的影响.由于预先保护了图像的边缘特征,在阈值去噪的时候,尽可以根据噪声方差加大阈值,而不必担心损害图像的边缘特征.

对图像来说，如果需要进行快速或实时传输以及大量存储，就需要对图像数据进行压缩。图像压缩研究的是寻找高压缩比的方法，保证在压缩后图像中有合适的信噪比，在压缩传输后能够恢复图像，在压缩、传输、恢复过程中保证图像失真小。

2 图像的噪声模型

图像的噪声大致可分为3类[3]: 感光照片上的颗粒噪声、光电转换过程中产生的光电子噪声和电子设备产生的热电子噪声。 对于颗粒噪声,可以用高斯白噪声作为模型; 对于光电子噪声,在光照较弱时,可以用具有泊松分布的随机变量作为模型,其标准差等于均值的平方根,在光照较强时,泊松分布趋向高斯分布,其标准差仍等于均值的平方根;对于热电子噪声,一般常用零均值的高斯白噪声作为模型。

因此,对于大多数图像处理的应用来说,经常采用零均值高斯白噪声作为图像的噪声模型。

3 图象的小波边缘检测方法

图象去噪方法,要求事先确定图象边缘特征的空间位置,以便在去噪时,能够有所回避,虽然已有许多边缘检测方法,如采用各种梯度算子( Roberts梯度算子、Sobel梯度算子、拉普拉斯算子或Prewitt梯度算子)的边缘检测方法[3] , 小波边缘检测方法[4-6] ,等等,但由于在去噪方面,采用了小波阈值去噪方法,因此为了与之配套,在边缘检测方面,也采用了小波边缘检测方法. 这样做的好处是,可以直接确定哪些小波系数对应着图象的边缘特征.

3.1 原理

小波变换的含义是把某一被称为基本小波的函数作位移τ后，再在不同尺度a下，与待分析的信号x(t)作内积，即

式中，a>0称为尺度因子，其作用是对基本小波函数φ(x)作伸缩，τ反映位移，其值可正可负，a和τ都是持续的变量，故又称为持续小波变换。在不同尺度下小波的持续时间随值的加大而增宽，幅度则与 反比减少，但波的形状保持不变。

等效频域表示为：

式中分别X(ω)和Ψ(ω)是x(t)、φ(t)的傅里叶变换。

根据图象小波边缘检测的理论 ,可以适当选择二维二进可分离小波,使得这样的小波可以看成是某一平滑函数θ( x , y )的偏导数:

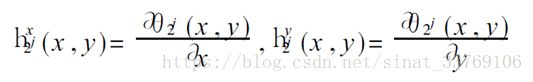
于是,图象f (x , y )在尺度2^j 下的小波变换可表示为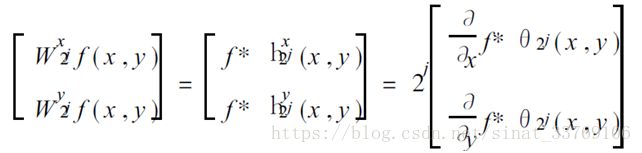

由此可见图象f (x , y )经过平滑后,在x 和y 方向上的偏导数就是图象在行和列方向上的小波变换. 因此,小波系数的局部极大值点可以刻画图象的突变点,也即图象的边缘特征点.

对于含加性高斯白噪声的图象,小波系数的极大值也可能对应着噪声点,而不是边缘特征点. 因此,在检测出小波系数的极大值后,还要去除与噪声点对应的小波系数.由于信号的Lipschi t z指数为正时,其小波变换随尺度的减小而减小, 而噪声的Lipschitz指数小于零时,其小波变换的平均值随尺度的减小而增加,因此,可以通过去除那些空间位置相同,但幅度随尺度减小反而增加的小波系数来消除部分噪声点,对于剩下的小波系数,沿着梯度的垂直方向(即边缘曲线的切线方向)进行串接,对于那些串接不起来的小波系数,也当作噪声点去除.

3.2 实现方法

在具体实现时,要注意以下3个问题:

(1) 小波变换所使用的离散滤波器,其长度不宜太长,否则会影响边缘提取的效果;

(2) 要妥善处理边界问题,本文采用镜像对称延拓来处理边界问题;

(3) 图象小波分解的次数不宜过多,因为次数愈多,边界问题的影响就会愈显著.

具体的实现步骤如下:

(1)   对图象f (x , y )先进行一次平滑预处理,其结果仍记为f(x,y) ;

(2)  记,对的每一行进行小波变换(这时, y 是参数, x 是变量) ,得到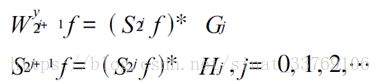

这里, j 表示尺度, Gj、Hj 表示小波变换所使用的离散滤波器。

(3)   找出每行的零交叉点,并根据这些零交叉点求出相邻零交叉点间的极大值点,记录这些极大值点.

(4)   去除那些空间位置相同,但幅值随尺度j减小反而增大的极大值点,因为这些极大值点通常是由噪声生成.剩下的极大值点即为行方向上图象边缘特征点的候选点,仍记为

(5)   对图象的列方向重复上述第1、2、3、4的步骤,得到列方向上图象边缘特征点的候选点,记为

(6)   沿着梯度的垂直方向,将图像在点(x,y)上的梯度的模和幅角相近的点串接成链,当链长超过一定阈值T 时,链上小波系数的位置就是图象在该尺度上的边缘特征点.

3.3 实验结果

图2 原始图像

图3 调整图像对比度及像素值

图4 第一次边缘提取

图5 第二次边缘提取

图6 第三次边缘提取

        再用Canny算子对图片进行边缘检测，并对比效果。

图7  Canny算子

图8 GUI显示

 

4 基于小波变换的图像压缩

4.1 基于小波变换的图像压缩的特点

长期以来，图像压缩编码利用离散余弦变换（DCT）作为主要的变换技术，并成功的应用于各种标准，比如JPEG、MPEG-1、MPEG-2。但是，在基于DCT图像变换编码中，人们将图像分为88像素或者1616像素的块来处理，从而容易出现方块效应与蚊式噪声。

小波变换是全局变换，在时域和频域都由良好的局部优化性能。小波变换将图像的像素解相关的变换系数进行编码，比经典编码的效率更高，而且几乎没有失真，在应用中易于考虑人类的视觉特性，从而成为图像压缩编码的主要技术之一。

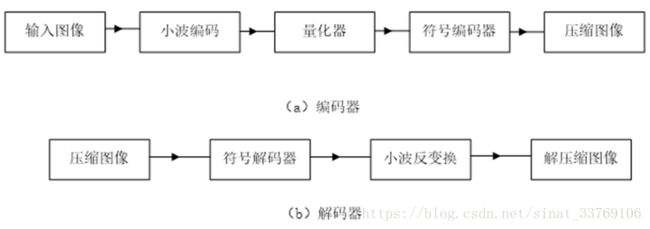
小波变换在信号的高频部分可以取得较好的时间分辨率：在信号的低频部分，可以取得较好的频率分辨率，从而能有效地从信号（如语音、图像等）中提取信息，达到数据压缩的目的。图9为小波编解码系统的框图。

图9 小波变换的编码器和解码器

4.2 图像压缩的实现

基于小波变换的图像压缩基本步骤如下：

①用小波对图像层分解并提取分解结构中的低频和高频系数

②各频率成分重构

③对第一层低频信息压缩

④对第二层低频信息压缩

实验结果如下：

 

5 结论

本文将小波变换应用于图像边缘检测和图像压缩中，确定了不受阈值去噪影响的小波系数，保证了图像的边缘特征在一定程度下不受损害。在图像编码处理中,对高频部分大多数系数分配较小的比特，达到了压缩的目的。

本文在小波变换的边缘检测应用中仍存在很多不足，效果不如Canny算子。在今后的工作中将会考虑改进方式，可以尝试找到优化的小波变换边缘检测方式。

基于小波变换的图像压缩虽然优于经典的压缩方法，被广泛使用。但是还可以在提高图像质量，提高压缩比，与人眼视觉特性相结合，与其他优秀的压缩方法相结合等方面深入研究。

主要参考文献：

1. 杨正远, 郑建宏. 小波在图象边缘检测中的应用[J]. 重庆邮电大学学报自然科学版, 1997(1).

2. 廖剑利. 基于小波变换的图像边缘检测方法研究[D]. 湖南大学, 2005.